【数学】1.1.2《棱柱、棱锥和棱台的结构特征(2)配套》课件(人教b版必修2)
文档属性
| 名称 | 【数学】1.1.2《棱柱、棱锥和棱台的结构特征(2)配套》课件(人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 52.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
1.1.2 棱柱、棱锥和棱台
的结构特征(二)
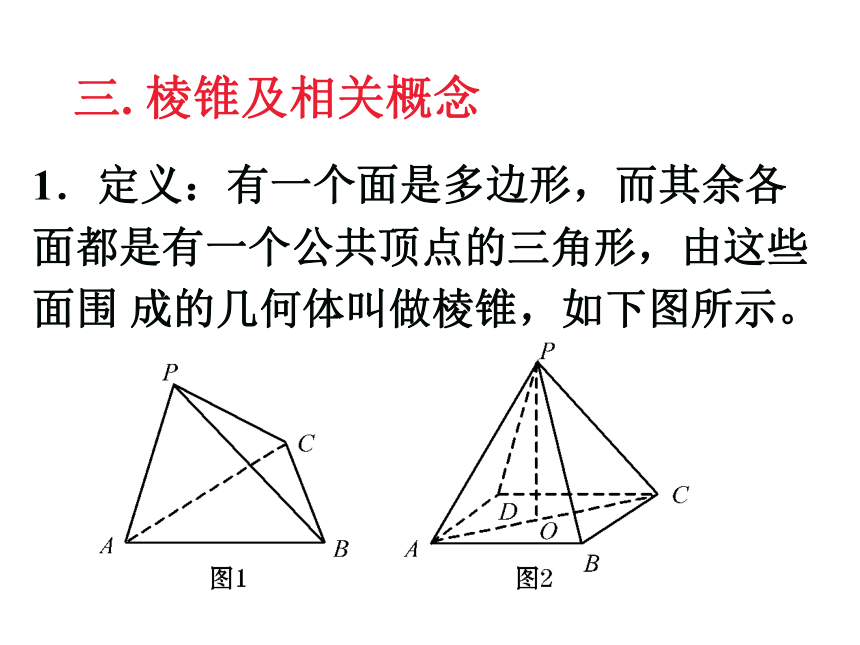
三. 棱锥及相关概念
1.定义:有一个面是多边形,而其余各面都是有一个公共顶点的三角形,由这些面围 成的几何体叫做棱锥,如下图所示。
棱锥的侧面
棱锥的顶点
棱锥的侧棱
棱锥的高
S
A
B
C
D
E
O
2.相关概念:
(1)棱锥中有公共顶点的各三角形叫做棱锥的侧面,如侧面 SAB、SAE 等;
棱锥的底面
(2)各侧面的公共顶点叫做棱锥的顶点,如顶点S、A、B、C 等;
(3)相邻两侧面的公共边叫做棱锥的侧棱,如侧棱SA、SB等;
(4)棱锥中的多边形叫做棱锥的底面,如底面ABC、ABCDE等;
(5)如果棱锥的底面水平放置,则顶点与过顶点的铅垂线与底面的交点之间的线段或距离,叫做棱锥的高,如SO.
3. 如何理解棱锥?
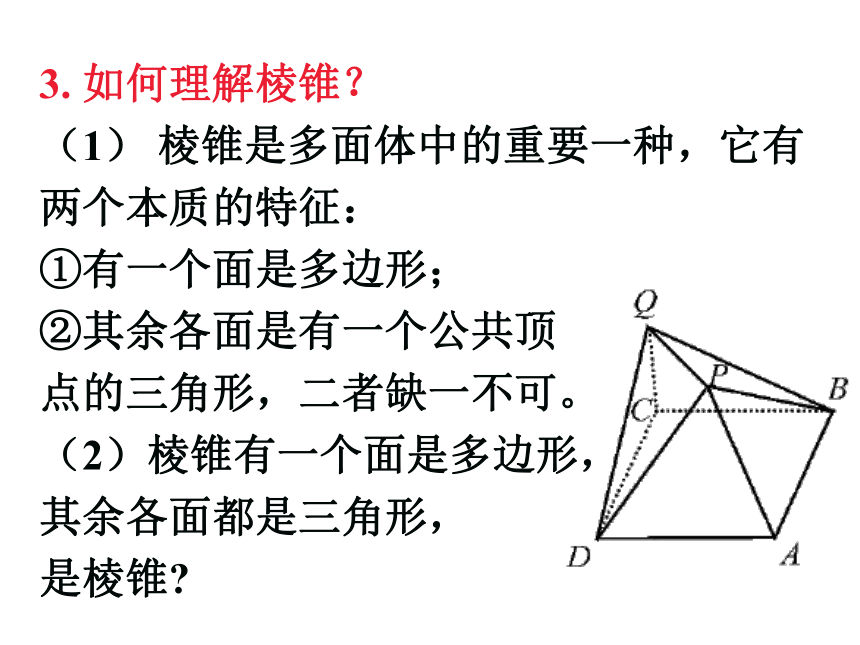
(1) 棱锥是多面体中的重要一种,它有两个本质的特征:
①有一个面是多边形;
②其余各面是有一个公共顶
点的三角形,二者缺一不可。
(2)棱锥有一个面是多边形,
其余各面都是三角形,
是棱锥
4.棱锥的分类:
(1)按底面多边形的边数分为三棱锥、四棱锥、五棱锥等,其中三棱锥又叫四面体!
三棱锥
四棱锥
五棱锥
(四面体)
(2)正棱锥:如果棱锥的底面是正多边形,并且水平放置, 它的顶点又在过正多边形中心的铅垂线上,则这个棱锥叫做正棱锥!
O
S
A
B
C
D
E
5.正棱锥的性质:
(1)正棱锥的各侧面都是全等的等腰三角形;
(2)等腰三角形底边上的高都相等,叫做棱锥的斜高!
6.棱锥的表示:
(1)用顶点和底面各顶点的字母表示棱锥:如三棱锥P-ABC,四棱锥S-ABCD.
(2)用对角面表示:如四棱锥可以用P-AC表示.
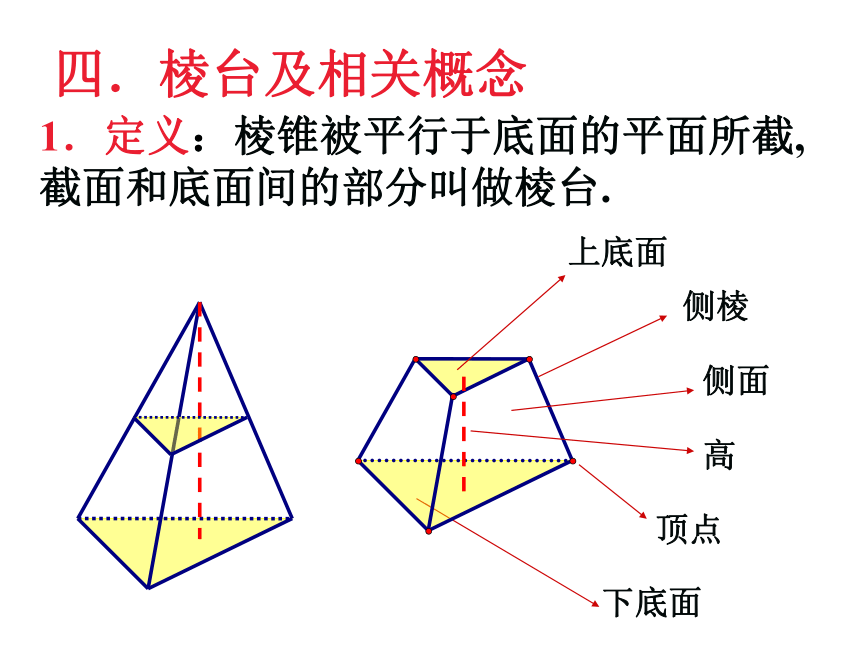
四.棱台及相关概念
1.定义:棱锥被平行于底面的平面所截,截面和底面间的部分叫做棱台.
下底面
上底面
侧面
侧棱
高
顶点
2.相关概念:
(1)棱台的下底面、上底面:原棱锥的底面和截面分别叫做棱台的下底面、上底面;
(2)棱台的侧面:棱台中除上、下底面以外的面叫做棱台的侧面;
(3)棱台的侧棱:相邻两侧面的公共边叫做棱台的侧棱;
(4)棱台的高:当棱台的底面水平放置时,铅垂线与两底面交点间的线段或距离叫做棱台的高。
3.棱台的分类:
(1)按底面多边形的边数分为三棱台、四棱台、五棱台等;
(2)正棱台:由正棱锥截得的棱台叫做正棱台。
正棱锥
正四棱台
4.正棱台的性质:
(1)各侧棱相等;
(2)正棱台的各侧面都是全等的等腰梯形;
(3)正棱台的斜高相等。
5.棱台的表示:
棱台可用表示上、下底面的字母来命名,如可以记 作 棱 台ABCD-A’B’C’D’,
或 记 作 棱 台AC’.
2.右图中 的几何体是不是棱台 为什么
棱柱、棱锥、棱台之间的关系
棱锥是当棱柱的一个底面收缩为一个点时形成的空间图形,
棱台则可以看成是用 一个平行于棱锥底面的平面截棱锥所得到的图形,
要注意的是棱台的各条侧棱延长后,将会交于一点,即棱台可以还原成棱锥.
例1.有四个命题:① 各侧面是全等的等腰三角形的四棱锥是正四棱锥;② 底面是正多边形的棱锥是正棱锥;③ 棱锥的所有侧面可能都是直角三角形;④ 四棱锥的四个侧面中可能四个都是直角三角形。其中正确的命题有 .
③ ④
解:设VO为正四棱锥V-ABCD的高,作OM⊥BC于点M,则M为BC中点,
连接OM、OB,则VO⊥OM,VO⊥OB.
例2. 已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为2 ,计算它的高和斜高。
因为底面正方形ABCD的面积是16,所以BC=4,MB=OM=2,
又因为VB= ,在Rt△VOB中,由勾股定理得
在Rt△VOM中,由勾股定理得
即正四棱锥的高为6,斜高为
练习题:
1.能保证棱锥是正棱锥的一个条件是( )
(A)底面为正多边形
(B)各侧棱都相等
(C)各侧面与底面都是全等的正三角形 (D)各侧面都是等腰三角形
C
2.若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )
(A)三棱锥 (B)四棱锥
(C)五棱锥 (D)六棱锥
D
3.过正方体三个顶点的截面截得一个正三棱锥,若正方体棱长为 a,则截得的正三棱锥的高为 。
4.正四面体棱长为 a,M,N为其两条相对棱的中点,则MN的长是 。
1.1.2 棱柱、棱锥和棱台
的结构特征(二)
三. 棱锥及相关概念
1.定义:有一个面是多边形,而其余各面都是有一个公共顶点的三角形,由这些面围 成的几何体叫做棱锥,如下图所示。
棱锥的侧面
棱锥的顶点
棱锥的侧棱
棱锥的高
S
A
B
C
D
E
O
2.相关概念:
(1)棱锥中有公共顶点的各三角形叫做棱锥的侧面,如侧面 SAB、SAE 等;
棱锥的底面
(2)各侧面的公共顶点叫做棱锥的顶点,如顶点S、A、B、C 等;
(3)相邻两侧面的公共边叫做棱锥的侧棱,如侧棱SA、SB等;
(4)棱锥中的多边形叫做棱锥的底面,如底面ABC、ABCDE等;
(5)如果棱锥的底面水平放置,则顶点与过顶点的铅垂线与底面的交点之间的线段或距离,叫做棱锥的高,如SO.
3. 如何理解棱锥?
(1) 棱锥是多面体中的重要一种,它有两个本质的特征:
①有一个面是多边形;
②其余各面是有一个公共顶
点的三角形,二者缺一不可。
(2)棱锥有一个面是多边形,
其余各面都是三角形,
是棱锥
4.棱锥的分类:
(1)按底面多边形的边数分为三棱锥、四棱锥、五棱锥等,其中三棱锥又叫四面体!
三棱锥
四棱锥
五棱锥
(四面体)
(2)正棱锥:如果棱锥的底面是正多边形,并且水平放置, 它的顶点又在过正多边形中心的铅垂线上,则这个棱锥叫做正棱锥!
O
S
A
B
C
D
E
5.正棱锥的性质:
(1)正棱锥的各侧面都是全等的等腰三角形;
(2)等腰三角形底边上的高都相等,叫做棱锥的斜高!
6.棱锥的表示:
(1)用顶点和底面各顶点的字母表示棱锥:如三棱锥P-ABC,四棱锥S-ABCD.
(2)用对角面表示:如四棱锥可以用P-AC表示.
四.棱台及相关概念
1.定义:棱锥被平行于底面的平面所截,截面和底面间的部分叫做棱台.
下底面
上底面
侧面
侧棱
高
顶点
2.相关概念:
(1)棱台的下底面、上底面:原棱锥的底面和截面分别叫做棱台的下底面、上底面;
(2)棱台的侧面:棱台中除上、下底面以外的面叫做棱台的侧面;
(3)棱台的侧棱:相邻两侧面的公共边叫做棱台的侧棱;
(4)棱台的高:当棱台的底面水平放置时,铅垂线与两底面交点间的线段或距离叫做棱台的高。
3.棱台的分类:
(1)按底面多边形的边数分为三棱台、四棱台、五棱台等;
(2)正棱台:由正棱锥截得的棱台叫做正棱台。
正棱锥
正四棱台
4.正棱台的性质:
(1)各侧棱相等;
(2)正棱台的各侧面都是全等的等腰梯形;
(3)正棱台的斜高相等。
5.棱台的表示:
棱台可用表示上、下底面的字母来命名,如可以记 作 棱 台ABCD-A’B’C’D’,
或 记 作 棱 台AC’.
2.右图中 的几何体是不是棱台 为什么
棱柱、棱锥、棱台之间的关系
棱锥是当棱柱的一个底面收缩为一个点时形成的空间图形,
棱台则可以看成是用 一个平行于棱锥底面的平面截棱锥所得到的图形,
要注意的是棱台的各条侧棱延长后,将会交于一点,即棱台可以还原成棱锥.
例1.有四个命题:① 各侧面是全等的等腰三角形的四棱锥是正四棱锥;② 底面是正多边形的棱锥是正棱锥;③ 棱锥的所有侧面可能都是直角三角形;④ 四棱锥的四个侧面中可能四个都是直角三角形。其中正确的命题有 .
③ ④
解:设VO为正四棱锥V-ABCD的高,作OM⊥BC于点M,则M为BC中点,
连接OM、OB,则VO⊥OM,VO⊥OB.
例2. 已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为2 ,计算它的高和斜高。
因为底面正方形ABCD的面积是16,所以BC=4,MB=OM=2,
又因为VB= ,在Rt△VOB中,由勾股定理得
在Rt△VOM中,由勾股定理得
即正四棱锥的高为6,斜高为
练习题:
1.能保证棱锥是正棱锥的一个条件是( )
(A)底面为正多边形
(B)各侧棱都相等
(C)各侧面与底面都是全等的正三角形 (D)各侧面都是等腰三角形
C
2.若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )
(A)三棱锥 (B)四棱锥
(C)五棱锥 (D)六棱锥
D
3.过正方体三个顶点的截面截得一个正三棱锥,若正方体棱长为 a,则截得的正三棱锥的高为 。
4.正四面体棱长为 a,M,N为其两条相对棱的中点,则MN的长是 。
