【数学】1.2.1《平面的基本性质与推论》课件(人教b版必修2)
文档属性
| 名称 | 【数学】1.2.1《平面的基本性质与推论》课件(人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 88.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:32 | ||
图片预览








文档简介
(共26张PPT)
1.2.1平面的基本性质与推论
一.平面的基本性质:
1.公理1:
①文字语言:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内 ;
②图形语言:
③符号语言:A∈l;B∈l,A∈α,B∈α
AB α.
练习:
(1)
。
(2)
。
公理1的作用有两个:(1)作为判断和证明直线是否在平面内的依据,即只需要看直线上是否有两个点在平面内就可以了;
(2)公理1可以用来检验某一个面是否为平面,检验的方法为:把一条直线在面内旋转,固定两个点在面内后,如果其他点也在面内,则该面为平面。
2.公理2:
①文字语言:经过不在同一条直线上的三点,有且只有一个平面,也可以说成不共线的三点确定一个平面。
②图形语言:
③符号语言:A、B、C三点不共线,有且只有一个平面α,使得A∈α,B∈α, C∈α.
如何理解公理2?
公理2是确定平面的条件.
深刻理解“有且只有”的含义,这里的“有”是说平面存在,“只有”是说平面惟一,“有且只有”强调平面存在并且惟一这两方面.
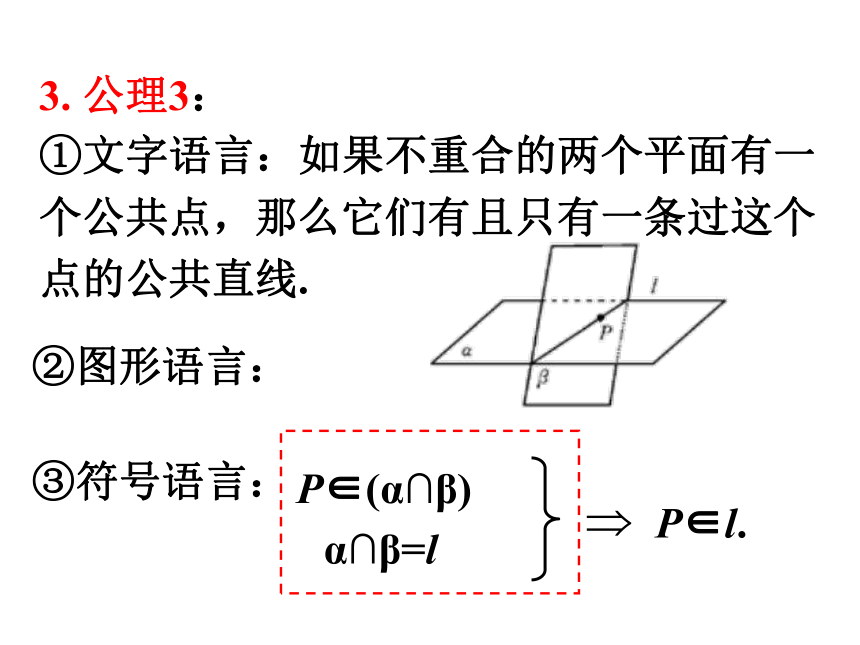
3. 公理3:
①文字语言:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.
②图形语言:
③符号语言:
P∈l.
P∈(α∩β)
α∩β=l
如何理解公理3?
(1) 公理3反映了平面与平面的位置关系,只要“两面共一点”,就有“两面共一线,且过这一点,线惟一”.
(2) 从集合的角度看,对于不重合的两个平面,只要他们有公共点,它们就是相交的位置关系,交集是一条直线.
(3) 公理3的作用:
其一判定两个平面是否相交;
其二可以判定点在直线上. 点是某两个平面的公共点,线是这两个平面的公共交线,则这点在线上.
因此它还是证明点共线或线共点,并且作为画截面的依据.
二. 平面基本性质的推论
文字语言 :经过一条直线和直线外的一点,有且只有一个平面.
图形语言:
符号语言:
a与A共属于平面α且平面α惟一 .
(1)推论1:
a是任意一条直线
点A a
(2)推论2:
文字语言 :经过两条相交直线,有且只有一个平面.
图形语言:
符号语言:
a,b共面于平面α,且α是惟一的 .
b是任意一条直线
a是任意一条直线
a∩b=A
(2)推论3:
文字语言 :经过两条平行直线,有且只有一个平面.
图形语言:
符号语言:
a,b共面于平面α,且α是惟一的 .
a,b是两条直线
a//b
m
图2
l
三、空间中两直线的位置关系
l
m
P
图1
从图中可见,直线 l 与 m 既不相交,也不平行。空间中直线之间的这种关系称为异面直线。
不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)
1、异面直线
判断:
(1)图中直线m和l是异面直线吗
α
β
l
m
m
l
(2) ,则a与b是异面直线吗?
(3) a,b不同在平面α内,则a与b是异面吗?
异面直线的画法:
通常用一个或两个平面来衬托, 异面直线不同在任何一个平面的特点.
(1)相交
(2)平行
只有一个公共点
没有公共点
在同一平面
m
l
2、空间中两直线的三种位置关系
(3)异面直线
m
P
l
没有公共点
不同在任一平面
m
l
P
探究:
H
G
C
A
D
B
E
F
G
H
E
F(B)
(C)
D
A
一个正方体的展开图如上,则AB,CD, EF,GH这四条线段所在的直线是异面直线的有几对 相交直线有几对 平行直线有几对
直线和平面位置关系的符号表示.
(1)点A在平面α内,记作A∈α,点B不在平面α内,记作B α;
(2)直线l在平面α内,记作l α,直线m不在平面α内,记作m α;
(3)平面α与平面β相交于直线l,记作α∩β=l;
(4)直线l和m相交于点A,记作l∩m={A},简记为l∩m=A.
例1.如图,平面ABEF记作α,平面ABCD记作β,根据图形填写:
(1)A∈α,B α,E α,
C α,D α;
(2)A∈β,B β,C β,
D β,E β,F β;
(3)α∩β= ;
∈
∈
∈
∈
∈
AB
例2.如图中△ABC,若AB、BC 在平面α内,判断AC 是否在平面α内?
解:∵ AB在平面α内,∴ A点一定在平面α内,又BC在平面α内,∴ C点一定在平面α内, ( 点A、点C都在平面α内,) 直线AC 在平面α内(公理1).
例3.(1)不共面的四点可以确定几个平面?
(2)三条直线两两平行,但不共面,它们可以确定几个平面?
(3)共点的三条直线可以确定几个平面?
4个
3个
1个或3个
例4.如图,在正方体ABCD-A1B1C1D1中,E、F分别为CC1和AA1上的中点,画出平面BED1F与平面ABCD的交线.
解:在平面AA1D1D 内,延长D1F,∵ D1F与DA不平行,因此D1F与DA 必相交于一点,设为P,
P
P
又∵D1F 平面BED1F,P在平面BED1F内.
则P∈D1F,P∈DA ,
AD 平面ABCD,P∈平面ABCD,
又B为平面ABCD与平面BED1F的公共点,
∴连结PB,PB 即为平面BED1F 与平面ABCD的交线.
例5. 如图所示,已知△ABC的三个顶点都不在平面α内,它的三边AB、BC、AC延长线后分别交平面α于点P、Q、R,
求证:点P、Q、R在同一条直线上.
证明:由已知AB的延长线交平面α于点P,根据公理3,平面ABC与平面α必相交于一条直线,设为l,
∵ P∈直线AB,P∈面ABC,又直线AB∩面α=P,∴ P∈面α.
∴ P是面ABC与面α的公共点,
∵ 面ABC∩面α=l,∴P∈l,
同理,Q∈l,R∈l,
∴ 点P、Q、R在同一条直线l上.
1.2.1平面的基本性质与推论
一.平面的基本性质:
1.公理1:
①文字语言:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内 ;
②图形语言:
③符号语言:A∈l;B∈l,A∈α,B∈α
AB α.
练习:
(1)
。
(2)
。
公理1的作用有两个:(1)作为判断和证明直线是否在平面内的依据,即只需要看直线上是否有两个点在平面内就可以了;
(2)公理1可以用来检验某一个面是否为平面,检验的方法为:把一条直线在面内旋转,固定两个点在面内后,如果其他点也在面内,则该面为平面。
2.公理2:
①文字语言:经过不在同一条直线上的三点,有且只有一个平面,也可以说成不共线的三点确定一个平面。
②图形语言:
③符号语言:A、B、C三点不共线,有且只有一个平面α,使得A∈α,B∈α, C∈α.
如何理解公理2?
公理2是确定平面的条件.
深刻理解“有且只有”的含义,这里的“有”是说平面存在,“只有”是说平面惟一,“有且只有”强调平面存在并且惟一这两方面.
3. 公理3:
①文字语言:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.
②图形语言:
③符号语言:
P∈l.
P∈(α∩β)
α∩β=l
如何理解公理3?
(1) 公理3反映了平面与平面的位置关系,只要“两面共一点”,就有“两面共一线,且过这一点,线惟一”.
(2) 从集合的角度看,对于不重合的两个平面,只要他们有公共点,它们就是相交的位置关系,交集是一条直线.
(3) 公理3的作用:
其一判定两个平面是否相交;
其二可以判定点在直线上. 点是某两个平面的公共点,线是这两个平面的公共交线,则这点在线上.
因此它还是证明点共线或线共点,并且作为画截面的依据.
二. 平面基本性质的推论
文字语言 :经过一条直线和直线外的一点,有且只有一个平面.
图形语言:
符号语言:
a与A共属于平面α且平面α惟一 .
(1)推论1:
a是任意一条直线
点A a
(2)推论2:
文字语言 :经过两条相交直线,有且只有一个平面.
图形语言:
符号语言:
a,b共面于平面α,且α是惟一的 .
b是任意一条直线
a是任意一条直线
a∩b=A
(2)推论3:
文字语言 :经过两条平行直线,有且只有一个平面.
图形语言:
符号语言:
a,b共面于平面α,且α是惟一的 .
a,b是两条直线
a//b
m
图2
l
三、空间中两直线的位置关系
l
m
P
图1
从图中可见,直线 l 与 m 既不相交,也不平行。空间中直线之间的这种关系称为异面直线。
不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)
1、异面直线
判断:
(1)图中直线m和l是异面直线吗
α
β
l
m
m
l
(2) ,则a与b是异面直线吗?
(3) a,b不同在平面α内,则a与b是异面吗?
异面直线的画法:
通常用一个或两个平面来衬托, 异面直线不同在任何一个平面的特点.
(1)相交
(2)平行
只有一个公共点
没有公共点
在同一平面
m
l
2、空间中两直线的三种位置关系
(3)异面直线
m
P
l
没有公共点
不同在任一平面
m
l
P
探究:
H
G
C
A
D
B
E
F
G
H
E
F(B)
(C)
D
A
一个正方体的展开图如上,则AB,CD, EF,GH这四条线段所在的直线是异面直线的有几对 相交直线有几对 平行直线有几对
直线和平面位置关系的符号表示.
(1)点A在平面α内,记作A∈α,点B不在平面α内,记作B α;
(2)直线l在平面α内,记作l α,直线m不在平面α内,记作m α;
(3)平面α与平面β相交于直线l,记作α∩β=l;
(4)直线l和m相交于点A,记作l∩m={A},简记为l∩m=A.
例1.如图,平面ABEF记作α,平面ABCD记作β,根据图形填写:
(1)A∈α,B α,E α,
C α,D α;
(2)A∈β,B β,C β,
D β,E β,F β;
(3)α∩β= ;
∈
∈
∈
∈
∈
AB
例2.如图中△ABC,若AB、BC 在平面α内,判断AC 是否在平面α内?
解:∵ AB在平面α内,∴ A点一定在平面α内,又BC在平面α内,∴ C点一定在平面α内, ( 点A、点C都在平面α内,) 直线AC 在平面α内(公理1).
例3.(1)不共面的四点可以确定几个平面?
(2)三条直线两两平行,但不共面,它们可以确定几个平面?
(3)共点的三条直线可以确定几个平面?
4个
3个
1个或3个
例4.如图,在正方体ABCD-A1B1C1D1中,E、F分别为CC1和AA1上的中点,画出平面BED1F与平面ABCD的交线.
解:在平面AA1D1D 内,延长D1F,∵ D1F与DA不平行,因此D1F与DA 必相交于一点,设为P,
P
P
又∵D1F 平面BED1F,P在平面BED1F内.
则P∈D1F,P∈DA ,
AD 平面ABCD,P∈平面ABCD,
又B为平面ABCD与平面BED1F的公共点,
∴连结PB,PB 即为平面BED1F 与平面ABCD的交线.
例5. 如图所示,已知△ABC的三个顶点都不在平面α内,它的三边AB、BC、AC延长线后分别交平面α于点P、Q、R,
求证:点P、Q、R在同一条直线上.
证明:由已知AB的延长线交平面α于点P,根据公理3,平面ABC与平面α必相交于一条直线,设为l,
∵ P∈直线AB,P∈面ABC,又直线AB∩面α=P,∴ P∈面α.
∴ P是面ABC与面α的公共点,
∵ 面ABC∩面α=l,∴P∈l,
同理,Q∈l,R∈l,
∴ 点P、Q、R在同一条直线l上.
