【数学】1.2.3《直线与平面垂直的判定》课件(人教b版必修2)
文档属性
| 名称 | 【数学】1.2.3《直线与平面垂直的判定》课件(人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
回顾复习:
旗杆与底面垂直
生活中的线面垂直现象:
大桥的桥柱与水面垂直
生活中有很多直线与平面垂直的实例,你能举出几个吗?
军人与地面垂直
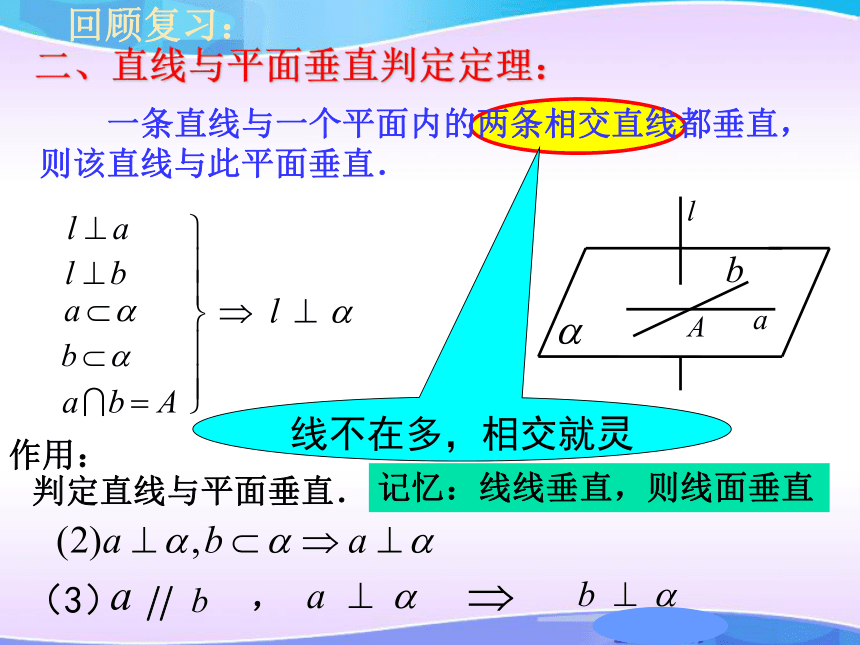
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
作用:
判定直线与平面垂直.
二、直线与平面垂直判定定理:
线不在多,相交就灵
记忆:线线垂直,则线面垂直
回顾复习:
,
(3)
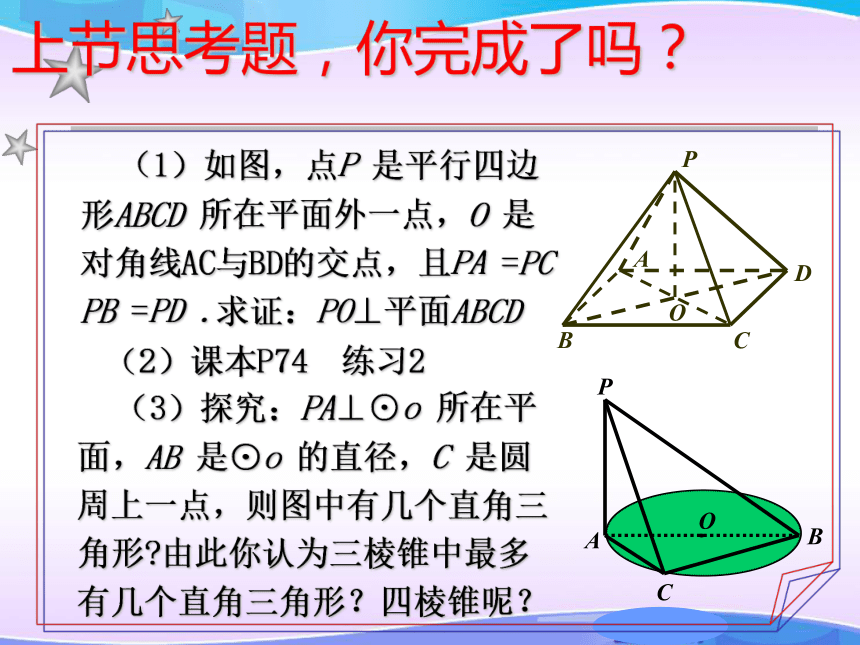
上节思考题,你完成了吗?
(1)如图,点P 是平行四边形ABCD 所在平面外一点,O 是
对角线AC与BD的交点,且PA =PC PB =PD .求证:PO⊥平面ABCD
C
A
B
D
O
P
P
A
B
C
O
(3)探究:PA⊥⊙o 所在平面,AB 是⊙o 的直径,C 是圆周上一点,则图中有几个直角三角形 由此你认为三棱锥中最多有几个直角三角形?四棱锥呢?
(2)课本P74 练习2
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示.
直线与平面的一条边垂直
新课讲解:
观察下面四个图,有什么结论?
(1)
P
(2)
P
(4)
P
(3)
P
(1)、(2):
(3)、(4):
过空间一点P作直线l的垂面只有一个;
过空间一点P作 的垂线只有一条;
P
A
O
四、直线和平面所成的角:
如图所示,一条直线PA和平面 相交,但不垂直,这
条直线叫这个平面的斜线,斜线和平面的交点A叫做斜足。
过斜线上斜足以外的一点P向平面引垂线PO ,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影。
斜线和射影所成的锐角叫做这条直线和平面所成的角。
斜线
斜足
射影
O
例题讲解:
如图,直四棱柱 (侧棱与底面垂直的棱柱成为直棱柱)中,底面四边形 满足什么条件时, ?
底面四边形 对角线相互垂直.
课堂练习:
1. 判断题:
( )
( )
( )
F
T
T
2. 求证:平面外一点与这个平面内各点的连线段中,
垂直于平面的线段最短。
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
知识小结
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
P
A
B
C
O
1、如图,圆O所在一平面为 ,AB是圆O 的直径,C 是圆周上一点,且PA AC, PA AB,求证:
(1)PA BC
(2)BC 平面PAC
(2)
2、如图,空间中直线L和三角形的两边AC,BC同时垂直,则这条直线和三角形的第三边AB的位置关系是( )
A 平行
B 垂直
C 相交
D 不确定
A
B
C
B
L
如果直线 l 与平面 内的任意一条直线都垂直,我们说直线 l 与平面 互相垂直,
记作 .
平面 的垂线
直线 l 的垂面
垂足
回顾复习:
旗杆与底面垂直
生活中的线面垂直现象:
大桥的桥柱与水面垂直
生活中有很多直线与平面垂直的实例,你能举出几个吗?
军人与地面垂直
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
作用:
判定直线与平面垂直.
二、直线与平面垂直判定定理:
线不在多,相交就灵
记忆:线线垂直,则线面垂直
回顾复习:
,
(3)
上节思考题,你完成了吗?
(1)如图,点P 是平行四边形ABCD 所在平面外一点,O 是
对角线AC与BD的交点,且PA =PC PB =PD .求证:PO⊥平面ABCD
C
A
B
D
O
P
P
A
B
C
O
(3)探究:PA⊥⊙o 所在平面,AB 是⊙o 的直径,C 是圆周上一点,则图中有几个直角三角形 由此你认为三棱锥中最多有几个直角三角形?四棱锥呢?
(2)课本P74 练习2
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示.
直线与平面的一条边垂直
新课讲解:
观察下面四个图,有什么结论?
(1)
P
(2)
P
(4)
P
(3)
P
(1)、(2):
(3)、(4):
过空间一点P作直线l的垂面只有一个;
过空间一点P作 的垂线只有一条;
P
A
O
四、直线和平面所成的角:
如图所示,一条直线PA和平面 相交,但不垂直,这
条直线叫这个平面的斜线,斜线和平面的交点A叫做斜足。
过斜线上斜足以外的一点P向平面引垂线PO ,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影。
斜线和射影所成的锐角叫做这条直线和平面所成的角。
斜线
斜足
射影
O
例题讲解:
如图,直四棱柱 (侧棱与底面垂直的棱柱成为直棱柱)中,底面四边形 满足什么条件时, ?
底面四边形 对角线相互垂直.
课堂练习:
1. 判断题:
( )
( )
( )
F
T
T
2. 求证:平面外一点与这个平面内各点的连线段中,
垂直于平面的线段最短。
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
知识小结
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
P
A
B
C
O
1、如图,圆O所在一平面为 ,AB是圆O 的直径,C 是圆周上一点,且PA AC, PA AB,求证:
(1)PA BC
(2)BC 平面PAC
(2)
2、如图,空间中直线L和三角形的两边AC,BC同时垂直,则这条直线和三角形的第三边AB的位置关系是( )
A 平行
B 垂直
C 相交
D 不确定
A
B
C
B
L
