【数学】2.3《圆与圆的位置关系》课件(新人教b版必修2)
文档属性
| 名称 | 【数学】2.3《圆与圆的位置关系》课件(新人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 183.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:32 | ||
图片预览








文档简介
(共22张PPT)
2.3 圆与圆的位置关系
一.两圆的位置关系
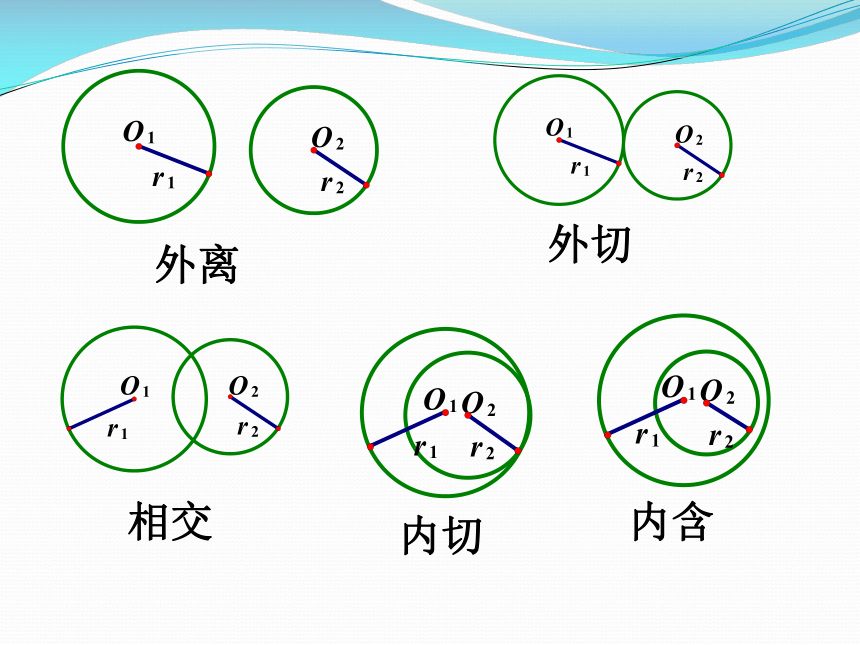
平面上两圆的位置关系有五种:
(1)两圆外离:两圆没有公共点;
(2)两圆外切:两圆有且仅有一个公共点;
(3)两圆相交:两圆有两个公共点;
(4)两圆内切:两圆有一个公共点;
(5)两圆内含:两圆没有公共点.
外离
外切
相交
内切
内含
二. 两圆位置关系的判断
已知圆C1:(x-a)2+(y-b)2=r12与圆C2:(x-c)2+(y-d)2=r22,它们的位置关系有两种判断方法:
(1)平面几何法判断圆与圆的位置关系公式:
第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系
两圆外离:r1+r2两圆外切:r1+r2=d;
两圆相交:|r1-r2|两圆内切:|r1-r2|=d;
两圆内含:|r1-r2|>d.
(2)代数法判断圆与圆的位置关系:
将两个圆方程联立,消去其中的一个未知数y或x,得关于x或y的一元二次方程.
若方程中△>0,则两圆相交;若方程中△=0,则两圆相切;若方程中△<0,两圆外离或内含.(此方法仅用于判断两个圆的位置关系,不适用于其他的二次曲线的位置关系的判断问题)
解:(1)两圆的方程分别变形为
(x-1)2+y2=4,(x-2)2+(y+1)2=2 .
所以两个圆心的坐标分别为(1,0)和(2,-1),两圆的圆心距d=|C1C2|= ,
例1. 判断下列两圆的位置关系:
(1)x2+y2-2x-3=0和x2+y2-4x+2y+3 =0;
(2)x2+y2-2y=0和x2+y2-2 x-6=0.
由|r1-r2|=2- ,r1+r2=2+ ,
因为2- < <2+ ,
所以这两个圆相交。
(2)x2+y2-2y=0和x2+y2-2 x-6=0.
(2)两圆的方程分别变形为
x2+(y-1)2=12,(x- )2+y2=32.
所以两圆内切。
由|r1-r2|=2,
所以两个圆心的坐标分别为(0,1)和( ,0),
两圆的圆心距d=|C1C2|=2,
例2.已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2+6x+2y-40=0 相交于A、B两点,求公共弦AB的长.
解法一:由两圆的方程相减,消去二次项得到一个二元一次方程,此方程即为公共弦AB所在的直线方程,4x+3y=10.
由
解得
或
所以两点的坐标是A(-2,6)、B(4,-2)
故|AB|=
圆C1的圆心C1(5,5 ),半径r1=5,
则|C1D|=
所以AB=2|AD|=
解法二:同解法一,先求出公共弦所在直线的方程:4x+3y=10.
过C1作C1D⊥AB于D.
例3.已知圆C与圆C1:x2+y2-2x=0相外切,并且与直线l:x+ y=0相切于点P(3,- ),求此圆C的方程.
解:设所求圆的圆心为C(a,b),半径长为r.
因为C(a,b)在过点P且与l垂直的直线上,
所以 ①.
又因为圆C与l相切于点P,
所以 ②
因为圆C与圆C1相外切,
所以 ③
由①得 a-b-4 =0
将其代入③得
解得 或
此时r=2或r=6,
所以所求圆C的方程为(x-4)2+y2=4,或x2+(y+4 )2=36 .
例4.已知圆C1:x2+y2-2mx+m2=4和圆C2:x2+y2+2x-4my=8-4m2相交,求实数m的取值范围.
解:由题意得C1(m,0),C2(-1,2m),r1=2,r2=3,
而两圆相交,有|r1-r2|<|C1C2|即1<(m+1)2+4m2<25,
解得
练习题:
1.圆x2+y2-2x=0和x2+y2+4y=0的位置关系是( )
(A)相离 (B)外切
(C)相交 (D)内切
C
2.两圆(x-a)2+(y-b)2=c2和(x-b)2+(y-a)2=c2相切,则( )
(A)(a-b)2=c2 (B)(a-b)2=2c2
(C)(a+b)2=c2 (D)(a+b)2=2c2
B
3.M={(x,y)| x2+y2≤4 },N={(x,y)| (x-1)2+(y-1)2=r2 (r>0)},若M∩N=N,则r的取值范围是( )
(A) (B)
(C) (D)
C
4.两圆x2+y2=r2与(x-3)2+(y+1)2=r2外切,则r是( )
(A) (B)
(C) (D)5
B
5.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是( )
(A)(x-4)2+(y-6)2=6
(B)(x±4)2+(y-6)2=6
(C)(x-4)2+(y-6)2=36
(D)(x±4)2+(y-6)2=36
D
6.圆x2+y2=1和圆(x-1)2+(y-1)2=1的公共弦长为 .
7.若圆:x2+y2-2ax+a2=2和x2+y2-2by +b2=1外离,则a、b满足的条件是 .
a2+b2≥3+2
2.3 圆与圆的位置关系
一.两圆的位置关系
平面上两圆的位置关系有五种:
(1)两圆外离:两圆没有公共点;
(2)两圆外切:两圆有且仅有一个公共点;
(3)两圆相交:两圆有两个公共点;
(4)两圆内切:两圆有一个公共点;
(5)两圆内含:两圆没有公共点.
外离
外切
相交
内切
内含
二. 两圆位置关系的判断
已知圆C1:(x-a)2+(y-b)2=r12与圆C2:(x-c)2+(y-d)2=r22,它们的位置关系有两种判断方法:
(1)平面几何法判断圆与圆的位置关系公式:
第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系
两圆外离:r1+r2
两圆相交:|r1-r2|
两圆内含:|r1-r2|>d.
(2)代数法判断圆与圆的位置关系:
将两个圆方程联立,消去其中的一个未知数y或x,得关于x或y的一元二次方程.
若方程中△>0,则两圆相交;若方程中△=0,则两圆相切;若方程中△<0,两圆外离或内含.(此方法仅用于判断两个圆的位置关系,不适用于其他的二次曲线的位置关系的判断问题)
解:(1)两圆的方程分别变形为
(x-1)2+y2=4,(x-2)2+(y+1)2=2 .
所以两个圆心的坐标分别为(1,0)和(2,-1),两圆的圆心距d=|C1C2|= ,
例1. 判断下列两圆的位置关系:
(1)x2+y2-2x-3=0和x2+y2-4x+2y+3 =0;
(2)x2+y2-2y=0和x2+y2-2 x-6=0.
由|r1-r2|=2- ,r1+r2=2+ ,
因为2- < <2+ ,
所以这两个圆相交。
(2)x2+y2-2y=0和x2+y2-2 x-6=0.
(2)两圆的方程分别变形为
x2+(y-1)2=12,(x- )2+y2=32.
所以两圆内切。
由|r1-r2|=2,
所以两个圆心的坐标分别为(0,1)和( ,0),
两圆的圆心距d=|C1C2|=2,
例2.已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2+6x+2y-40=0 相交于A、B两点,求公共弦AB的长.
解法一:由两圆的方程相减,消去二次项得到一个二元一次方程,此方程即为公共弦AB所在的直线方程,4x+3y=10.
由
解得
或
所以两点的坐标是A(-2,6)、B(4,-2)
故|AB|=
圆C1的圆心C1(5,5 ),半径r1=5,
则|C1D|=
所以AB=2|AD|=
解法二:同解法一,先求出公共弦所在直线的方程:4x+3y=10.
过C1作C1D⊥AB于D.
例3.已知圆C与圆C1:x2+y2-2x=0相外切,并且与直线l:x+ y=0相切于点P(3,- ),求此圆C的方程.
解:设所求圆的圆心为C(a,b),半径长为r.
因为C(a,b)在过点P且与l垂直的直线上,
所以 ①.
又因为圆C与l相切于点P,
所以 ②
因为圆C与圆C1相外切,
所以 ③
由①得 a-b-4 =0
将其代入③得
解得 或
此时r=2或r=6,
所以所求圆C的方程为(x-4)2+y2=4,或x2+(y+4 )2=36 .
例4.已知圆C1:x2+y2-2mx+m2=4和圆C2:x2+y2+2x-4my=8-4m2相交,求实数m的取值范围.
解:由题意得C1(m,0),C2(-1,2m),r1=2,r2=3,
而两圆相交,有|r1-r2|<|C1C2|
解得
练习题:
1.圆x2+y2-2x=0和x2+y2+4y=0的位置关系是( )
(A)相离 (B)外切
(C)相交 (D)内切
C
2.两圆(x-a)2+(y-b)2=c2和(x-b)2+(y-a)2=c2相切,则( )
(A)(a-b)2=c2 (B)(a-b)2=2c2
(C)(a+b)2=c2 (D)(a+b)2=2c2
B
3.M={(x,y)| x2+y2≤4 },N={(x,y)| (x-1)2+(y-1)2=r2 (r>0)},若M∩N=N,则r的取值范围是( )
(A) (B)
(C) (D)
C
4.两圆x2+y2=r2与(x-3)2+(y+1)2=r2外切,则r是( )
(A) (B)
(C) (D)5
B
5.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是( )
(A)(x-4)2+(y-6)2=6
(B)(x±4)2+(y-6)2=6
(C)(x-4)2+(y-6)2=36
(D)(x±4)2+(y-6)2=36
D
6.圆x2+y2=1和圆(x-1)2+(y-1)2=1的公共弦长为 .
7.若圆:x2+y2-2ax+a2=2和x2+y2-2by +b2=1外离,则a、b满足的条件是 .
a2+b2≥3+2
