【数学】2.3《直线与圆的位置关系》课件(人教b版必修2)
文档属性
| 名称 | 【数学】2.3《直线与圆的位置关系》课件(人教b版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:42 | ||
图片预览







文档简介
(共28张PPT)
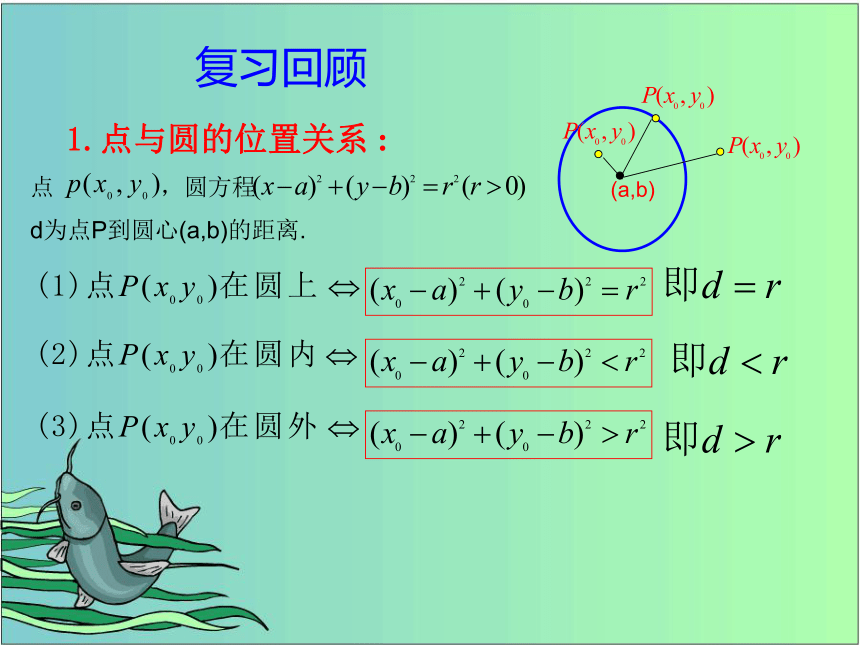
1.点与圆的位置关系 :
复习回顾
点 ,圆方程
d为点P到圆心(a,b)的距离.
(a,b)
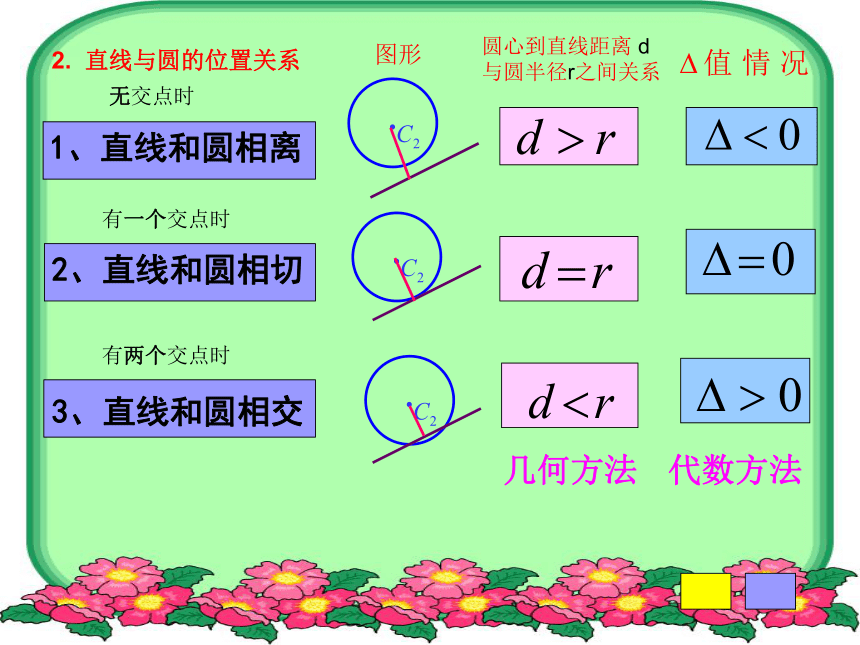
1、直线和圆相离
2、直线和圆相切
3、直线和圆相交
2. 直线与圆的位置关系
图形
圆心到直线距离 d 与圆半径r之间关系
几何方法
代数方法
无交点时
有一个交点时
有两个交点时
反馈练习
已知直线方程为 ,圆方程为
则当m为何值时,直线与圆(1)相切 ; (2)相离 ;(3)相交
解:由圆方程知圆心为(1,0),半径为1
由已知圆心到直线距离
(1)直线与圆相切时,d=1
(2)直线与圆相离时,d>1
(3)直线与圆相l交时,d<1
例1.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的
切线,切点为A、B。
求切线直线PA、PB的方程;
解:
1
2
2
1
-1
-1
O
A
B
A. 1或-1 B. 2,或-2 C. 1 D. -1
反馈练习
D
x
y
O
x
y
O
(2)
x
y
O
x
y
O
3.
反馈练习
3.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的切线,
切点为A、B,则直线AB为
4. 直线被圆截得的弦长的求法:
(1)几何方法:
运用弦心距 d 、半径r 及弦的一半构成的直
角三角形,计算弦长
(2)代数方法:
A
B
r
d
因此所证命题成立
解法1:
代 数 方 法
例题分析
A
B
l
解法2:(1)由圆方程可知,圆心为(0,1),半径为 r =
则 圆心到直线 l 的距离为
因此所证命题成立
(2)由平面解析几何的垂径定理可知
r
d
几何方法
l
A
B
解:
(2)如图,有平面几何垂径定理知
x
y
0
r
d
变式演练
代数解法
变式演练
解:将圆的方程写成标准形式,得
如图2-3-9,因为直线l 被圆所截得的弦长是 所以
弦心距为
即圆心到所求直线 l 的距离为 。
根据点到直线的距离公式,得到圆心到直线 l 的距离
所以,所求直线 l 有两条,方程分别为
l
已知圆O′的圆心在y轴上,截直线l1:3x+4y+3=0所得弦长为8,且与直线l2:3x-4y+37=0相切,求圆O′的方程。
解:
例题分析
x
y
O
变式演练
x
y
O
变式演练
o
y
x
.
C
A
B
例题分析
例题分析
1.直线与圆的位置关系:
3. 直线被圆截得的弦长的求法:
相离、相切、相交
判断方法:
几何方法、代数方法.
根据 P 点在圆外、圆上而不同.
(1)几何方法:
(2) 代数方法:
高考命题研究
直线与圆的位置关系一直是高考考查的热点,从近两年高考命题
情况来看,涉及本节知识的考题多为基础题,以选择题和填空题形式
出现有时也有综合性较强的解答题,解决直线与圆的位置关系问题时,
要联系圆的几何性质,利用有关图形的几何特征,尽可能简化运算。
如上图,某城市中的高空观览车的高度是100米,
在离观览车约150米处有一高建筑物,某人在离
建筑物100米的地方刚好可以看到观览车,你能
根据上述数据求出该建筑物的高度吗?
课后 思考题
150
100
100
1.点与圆的位置关系 :
复习回顾
点 ,圆方程
d为点P到圆心(a,b)的距离.
(a,b)
1、直线和圆相离
2、直线和圆相切
3、直线和圆相交
2. 直线与圆的位置关系
图形
圆心到直线距离 d 与圆半径r之间关系
几何方法
代数方法
无交点时
有一个交点时
有两个交点时
反馈练习
已知直线方程为 ,圆方程为
则当m为何值时,直线与圆(1)相切 ; (2)相离 ;(3)相交
解:由圆方程知圆心为(1,0),半径为1
由已知圆心到直线距离
(1)直线与圆相切时,d=1
(2)直线与圆相离时,d>1
(3)直线与圆相l交时,d<1
例1.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的
切线,切点为A、B。
求切线直线PA、PB的方程;
解:
1
2
2
1
-1
-1
O
A
B
A. 1或-1 B. 2,或-2 C. 1 D. -1
反馈练习
D
x
y
O
x
y
O
(2)
x
y
O
x
y
O
3.
反馈练习
3.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的切线,
切点为A、B,则直线AB为
4. 直线被圆截得的弦长的求法:
(1)几何方法:
运用弦心距 d 、半径r 及弦的一半构成的直
角三角形,计算弦长
(2)代数方法:
A
B
r
d
因此所证命题成立
解法1:
代 数 方 法
例题分析
A
B
l
解法2:(1)由圆方程可知,圆心为(0,1),半径为 r =
则 圆心到直线 l 的距离为
因此所证命题成立
(2)由平面解析几何的垂径定理可知
r
d
几何方法
l
A
B
解:
(2)如图,有平面几何垂径定理知
x
y
0
r
d
变式演练
代数解法
变式演练
解:将圆的方程写成标准形式,得
如图2-3-9,因为直线l 被圆所截得的弦长是 所以
弦心距为
即圆心到所求直线 l 的距离为 。
根据点到直线的距离公式,得到圆心到直线 l 的距离
所以,所求直线 l 有两条,方程分别为
l
已知圆O′的圆心在y轴上,截直线l1:3x+4y+3=0所得弦长为8,且与直线l2:3x-4y+37=0相切,求圆O′的方程。
解:
例题分析
x
y
O
变式演练
x
y
O
变式演练
o
y
x
.
C
A
B
例题分析
例题分析
1.直线与圆的位置关系:
3. 直线被圆截得的弦长的求法:
相离、相切、相交
判断方法:
几何方法、代数方法.
根据 P 点在圆外、圆上而不同.
(1)几何方法:
(2) 代数方法:
高考命题研究
直线与圆的位置关系一直是高考考查的热点,从近两年高考命题
情况来看,涉及本节知识的考题多为基础题,以选择题和填空题形式
出现有时也有综合性较强的解答题,解决直线与圆的位置关系问题时,
要联系圆的几何性质,利用有关图形的几何特征,尽可能简化运算。
如上图,某城市中的高空观览车的高度是100米,
在离观览车约150米处有一高建筑物,某人在离
建筑物100米的地方刚好可以看到观览车,你能
根据上述数据求出该建筑物的高度吗?
课后 思考题
150
100
100
