【数学】2.4.4《平面与平面垂直的性质》课件(新人教b版必修2)
文档属性
| 名称 | 【数学】2.4.4《平面与平面垂直的性质》课件(新人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:42 | ||
图片预览



文档简介
(共16张PPT)
2.4.4 平面与平面垂直的性质
问题提出
1.平面与平面垂直的定义是什么?如何判定平面与平面垂直?
2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?
定义和判定定理
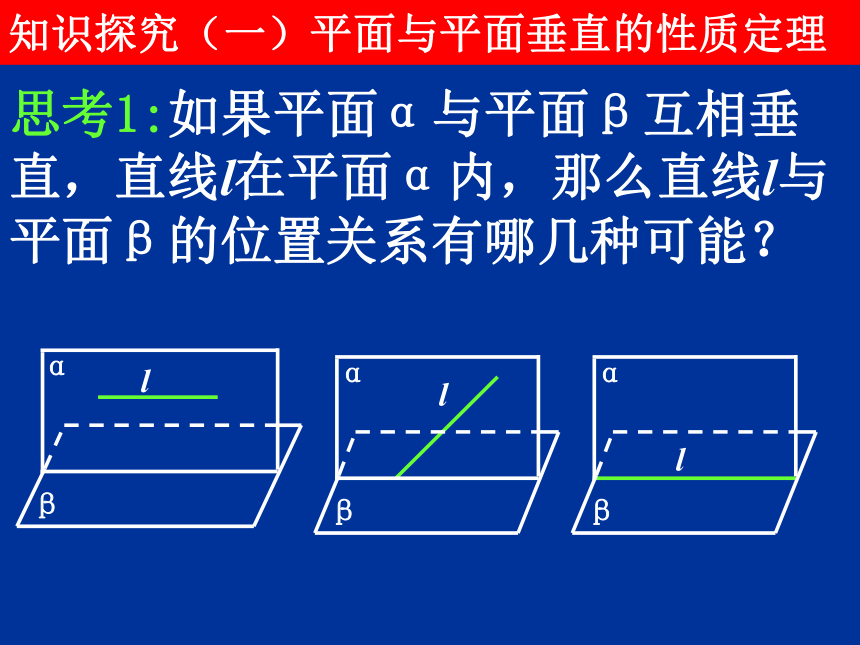
知识探究(一)平面与平面垂直的性质定理
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
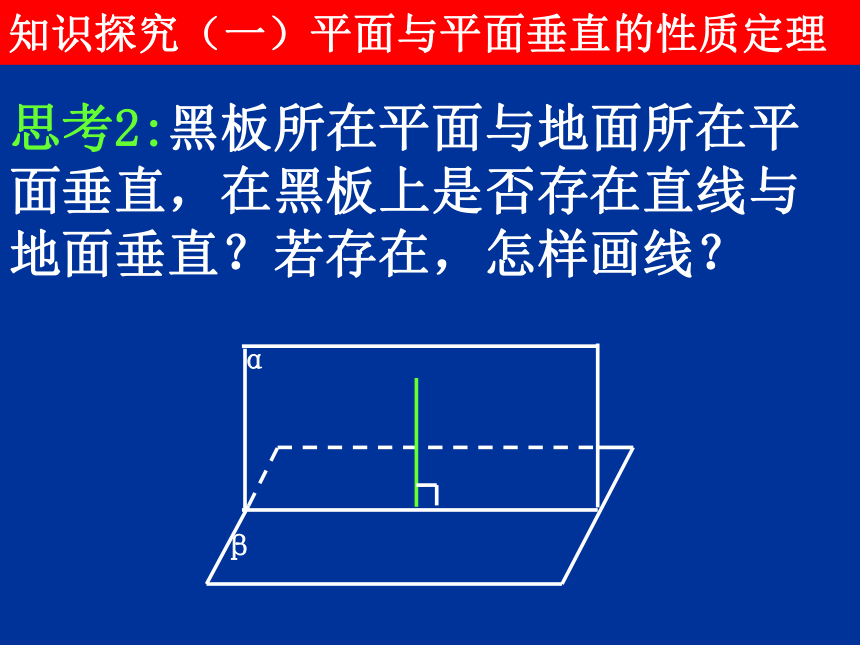
知识探究(一)平面与平面垂直的性质定理
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
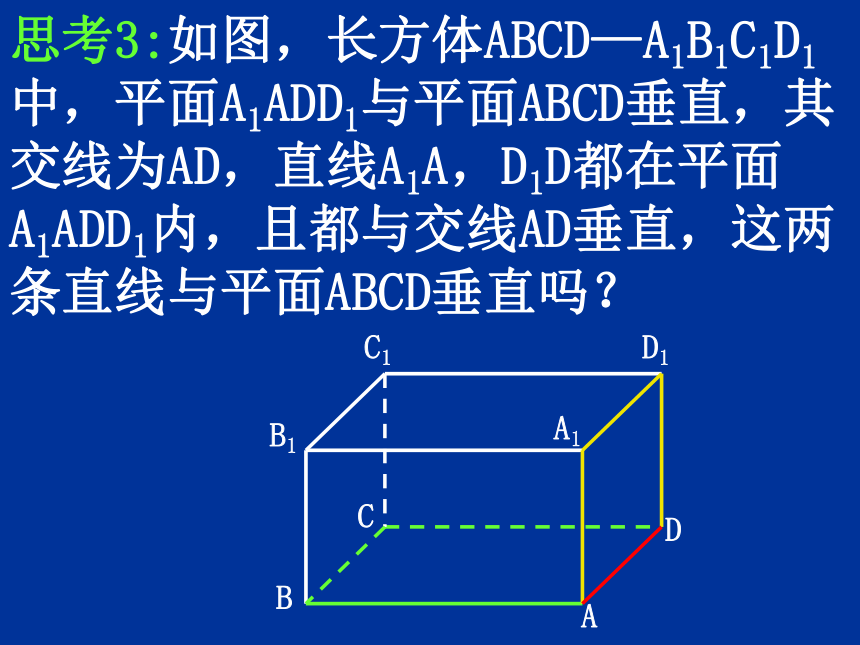
思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?
A
A1
B
C
D
B1
C1
D1
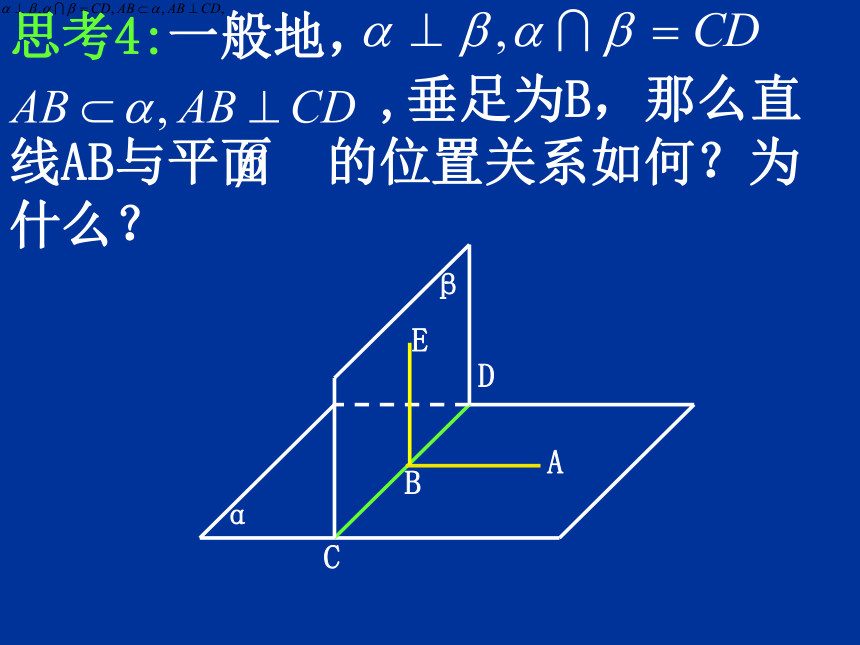
思考4:一般地,
,垂足为B,那么直线AB与平面 的位置关系如何?为什么?
α
β
A
B
D
C
E
思考5:据上分析可得什么定理?试用文字语言表述之.
定理 若两个平面互相垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
α
β
A
B
D
C
思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?该定理在实际应用中有何理论作用?
α
β
l
m
知识探究(二)平面与平面垂直的性质探究
思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.
B
α
β
A
思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.该性质在实际应用中有何理论作用?
B
α
β
A
思考3:对于三个平面α、β、γ,如果α⊥γ,β⊥γ, ,那么直线l与平面γ的位置关系如何?为什么?
α
β
γ
l
a
b
思考4:上述结论如何用文字语言表述?该性质在实际应用中有何理论作用?
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
γ
l
理论迁移
例1 如图,已知α⊥β,l⊥β,
,试判断直线l与平面α的位置关系,并说明理由.
α
β
l
m
a
例2 如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角.
P
A
B
C
D
E
作业:
P73练习:1,2.(做书上)
P73习题2.3A组:2.
P74习题2.3B组:3.
2.4.4 平面与平面垂直的性质
问题提出
1.平面与平面垂直的定义是什么?如何判定平面与平面垂直?
2.平面与平面垂直的判定定理,解决了两个平面垂直的条件问题;反之,在平面与平面垂直的条件下,能得到哪些结论?
定义和判定定理
知识探究(一)平面与平面垂直的性质定理
思考1:如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
α
β
l
l
α
β
l
α
β
知识探究(一)平面与平面垂直的性质定理
思考2:黑板所在平面与地面所在平面垂直,在黑板上是否存在直线与地面垂直?若存在,怎样画线?
α
β
思考3:如图,长方体ABCD—A1B1C1D1中,平面A1ADD1与平面ABCD垂直,其交线为AD,直线A1A,D1D都在平面A1ADD1内,且都与交线AD垂直,这两条直线与平面ABCD垂直吗?
A
A1
B
C
D
B1
C1
D1
思考4:一般地,
,垂足为B,那么直线AB与平面 的位置关系如何?为什么?
α
β
A
B
D
C
E
思考5:据上分析可得什么定理?试用文字语言表述之.
定理 若两个平面互相垂直,则在一个平面内垂直交线的直线与另一个平面垂直.
α
β
A
B
D
C
思考6:上述定理通常叫做两平面垂直的性质定理,结合下图,如何用符号语言描述这个定理?该定理在实际应用中有何理论作用?
α
β
l
m
知识探究(二)平面与平面垂直的性质探究
思考1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.
B
α
β
A
思考2:上述分析表明:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,必在这个平面内.该性质在实际应用中有何理论作用?
B
α
β
A
思考3:对于三个平面α、β、γ,如果α⊥γ,β⊥γ, ,那么直线l与平面γ的位置关系如何?为什么?
α
β
γ
l
a
b
思考4:上述结论如何用文字语言表述?该性质在实际应用中有何理论作用?
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
α
β
γ
l
理论迁移
例1 如图,已知α⊥β,l⊥β,
,试判断直线l与平面α的位置关系,并说明理由.
α
β
l
m
a
例2 如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角.
P
A
B
C
D
E
作业:
P73练习:1,2.(做书上)
P73习题2.3A组:2.
P74习题2.3B组:3.
