28.1 锐角三角函数(共4课时)
文档属性
| 名称 | 28.1 锐角三角函数(共4课时) |  | |
| 格式 | zip | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 20:28:01 | ||
图片预览




文档简介
28锐角三角函数
28.1.1正弦
[教学课时]1课时
[教学目标]
1、理解在直角三角形中,当锐角的度数固定时,它的对边与斜边的比值就固定下来了;
2、逐步培养学生会观察、比较、分析、概括等逻辑思维能力.
[教学重点]
使学生知道当锐角固定时,它的对边与斜边的比值也是固定的这一事实。
[教学难点]
理解正弦(sinA)概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实。
[教学过程]
一、知识回顾
归纳:在一个角为30°的直角三角形中,30°的对边与斜边之比都为1:2(与这个直角三角形的大小无关)。
二、 新课讲解
问题: 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
思考:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,30°角的对边与斜边的比值 。
结论:直角三角形中,45°角的对边与斜边的比值 。
结论:直角三角形中,60°角的对边与斜边的比值 。
探究活动:
正弦函数概念:
三、巩固提高
例:如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值。
学生活动设计:同学之间对比你们的结论,汇报讨论结果。
教师活动设计:
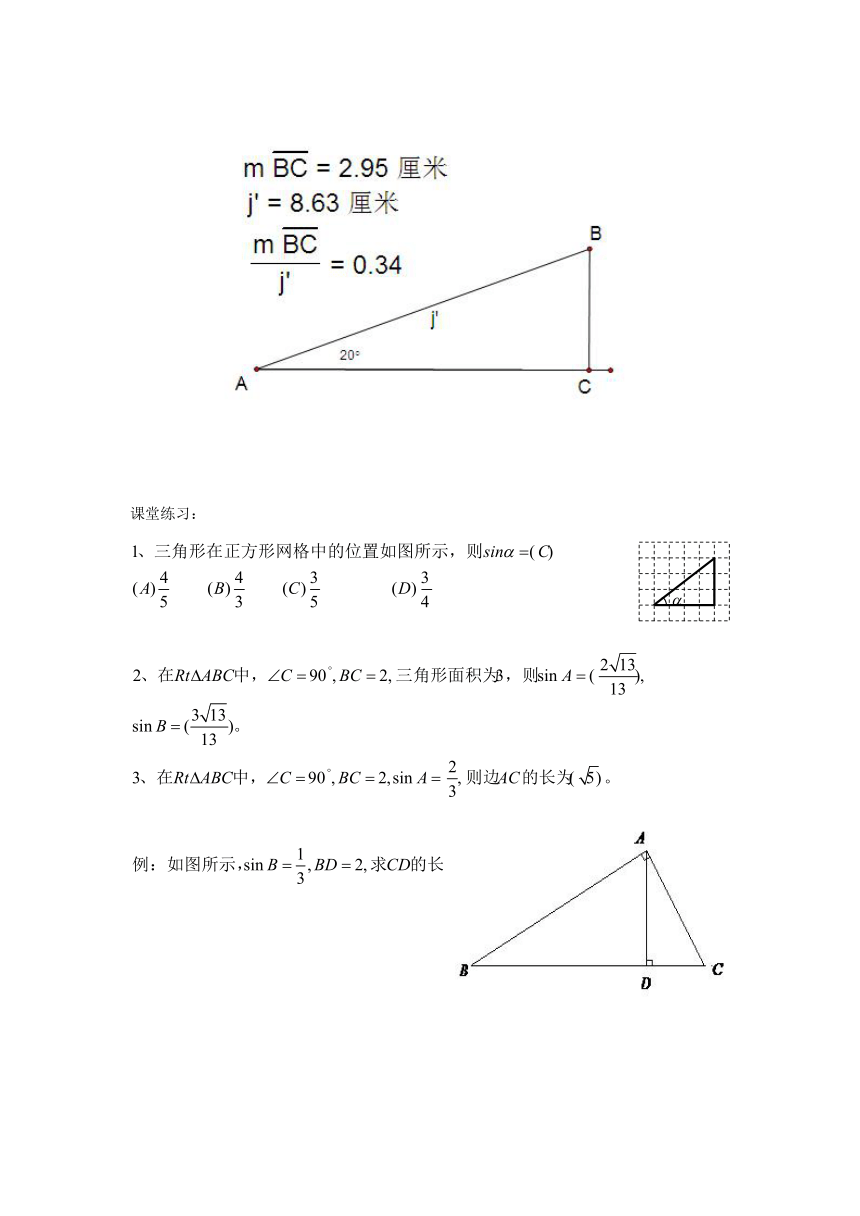
课堂练习:
四、课堂小结
本节课在复习勾股定理及含30°角直角三角形的性质基础上,通过动手实验、证明,我们发现,只要直角三角形的锐角固定,它的对边与斜边的比值也是固定的。在这个基础上我们给出了一个角正弦的定义。
五、布置作业
1、复习教材P74到P77;
2、预习余弦、正切的定义。
28锐角三角函数
28.1.2余弦、正切
[教学课时]1课时
[教学目标]
1、感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实;
2、逐步培养学生观察、比较、分析、概括的思维能力。
[教学重点]
理解余弦、正切的概念。
[教学难点]
熟练运用锐角三角函数的概念进行有关计算。
[教学过程]
一、复习回顾
1、我们是怎样定义直角三角形中一个锐角的正弦的?
2、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:
当锐角A确定时,
∠A的邻边与斜边的比会不会随着直角三角形的变大而变化?
∠A的对边与邻边的比会不会随着直角三角形的变大而变化?
探究活动:
二、新课讲解
类似于正弦的情况,
如图在Rt△ABC中,∠C=90°,当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的。
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= 。
(教师讲解并板书):锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数。
三、巩固提高
熟练掌握两个特殊的直角三角形:锐角为30度的和等腰直角三角形
课堂练习:完成课本P78 练习1、2、3
补充练习:
本题主要考查锐解三角函数的定义,同学们只要依据
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件
四、课堂小结
熟练掌握两个特殊的直角三角形:锐角为30度的;等腰直角三角形
五、布置作业
教材P82页 习题28.1复习巩固第1题、第2题.(只做与正弦、余弦、正切有关的部分)
第二十八章 锐角三角函数
28.1.3特殊角三角函数值
[教学课时]1课时
[教学目标]
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
2、能熟练计算含有30°、45°、60°角的三角函数的运算式
[教学重点]
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式
[教学难点]
30°、45°、60°角的三角函数值的推导过程
[教学过程]
一、复习回顾
一个直角三角形中,一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、巩固提高
师生活动设计:
思考:两块三角尺中有几个不同的锐角?是多少度?你能分别求出这几个锐角的正弦值、余弦值和正切值吗?
教师点拨:
归纳结果:
锐角三角函数
课堂练习:教材P80,1,2
师生活动设计:
练习:教材P81,练习1、2
探究活动:
教材 P83,第9题
锐角 … … …
探究活动:
三、课堂小结
锐角的三角函数值仅仅与该角的大小有关系,如锐角A的正切值,你可以做出一个角大小为A的直角三角形,A的正切值等于A的对边与邻边长度的比值;如果改变该直角三角形的大小,变形后的直角三角形与原来的直角三角形是相似的,所以比值是不变的。
四、布置作业
教材P82,习题28.1,3,4,5,6,7,8
28锐角三角函数
28.1.4锐角三角函数小结
[教学课时]1课时
[教学目标]
1、感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实;
2、逐步培养学生观察、比较、分析、概括的思维能力。
[教学重点]
理解余弦、正切的概念。
[教学难点]
熟练运用锐角三角函数的概念进行有关计算。
[教学过程]
一、复习回顾
二、巩固提高
例例2
思考:∠EDC转化到
一个直角三角形中,再
根据正切的定义求值。
设左边三角板的最短的边长为1;设右边三角板的一条直角边为1
设左边三角板的最短的边长为1;设右边三角板的一条直角边为1
28.1.1正弦
[教学课时]1课时
[教学目标]
1、理解在直角三角形中,当锐角的度数固定时,它的对边与斜边的比值就固定下来了;
2、逐步培养学生会观察、比较、分析、概括等逻辑思维能力.
[教学重点]
使学生知道当锐角固定时,它的对边与斜边的比值也是固定的这一事实。
[教学难点]
理解正弦(sinA)概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实。
[教学过程]
一、知识回顾
归纳:在一个角为30°的直角三角形中,30°的对边与斜边之比都为1:2(与这个直角三角形的大小无关)。
二、 新课讲解
问题: 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
思考:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边的比值是一个定值吗?如果是,是多少?
结论:直角三角形中,30°角的对边与斜边的比值 。
结论:直角三角形中,45°角的对边与斜边的比值 。
结论:直角三角形中,60°角的对边与斜边的比值 。
探究活动:
正弦函数概念:
三、巩固提高
例:如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值。
学生活动设计:同学之间对比你们的结论,汇报讨论结果。
教师活动设计:
课堂练习:
四、课堂小结
本节课在复习勾股定理及含30°角直角三角形的性质基础上,通过动手实验、证明,我们发现,只要直角三角形的锐角固定,它的对边与斜边的比值也是固定的。在这个基础上我们给出了一个角正弦的定义。
五、布置作业
1、复习教材P74到P77;
2、预习余弦、正切的定义。
28锐角三角函数
28.1.2余弦、正切
[教学课时]1课时
[教学目标]
1、感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实;
2、逐步培养学生观察、比较、分析、概括的思维能力。
[教学重点]
理解余弦、正切的概念。
[教学难点]
熟练运用锐角三角函数的概念进行有关计算。
[教学过程]
一、复习回顾
1、我们是怎样定义直角三角形中一个锐角的正弦的?
2、在Rt△ABC中,∠C=90°,当锐角A确定时,
∠A的对边与斜边的比是 ,
现在我们要问:
当锐角A确定时,
∠A的邻边与斜边的比会不会随着直角三角形的变大而变化?
∠A的对边与邻边的比会不会随着直角三角形的变大而变化?
探究活动:
二、新课讲解
类似于正弦的情况,
如图在Rt△ABC中,∠C=90°,当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的。
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= 。
(教师讲解并板书):锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数。
三、巩固提高
熟练掌握两个特殊的直角三角形:锐角为30度的和等腰直角三角形
课堂练习:完成课本P78 练习1、2、3
补充练习:
本题主要考查锐解三角函数的定义,同学们只要依据
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件
四、课堂小结
熟练掌握两个特殊的直角三角形:锐角为30度的;等腰直角三角形
五、布置作业
教材P82页 习题28.1复习巩固第1题、第2题.(只做与正弦、余弦、正切有关的部分)
第二十八章 锐角三角函数
28.1.3特殊角三角函数值
[教学课时]1课时
[教学目标]
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
2、能熟练计算含有30°、45°、60°角的三角函数的运算式
[教学重点]
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式
[教学难点]
30°、45°、60°角的三角函数值的推导过程
[教学过程]
一、复习回顾
一个直角三角形中,一个锐角正弦是怎么定义的?
一个锐角余弦是怎么定义的?
一个锐角正切是怎么定义的?
二、巩固提高
师生活动设计:
思考:两块三角尺中有几个不同的锐角?是多少度?你能分别求出这几个锐角的正弦值、余弦值和正切值吗?
教师点拨:
归纳结果:
锐角三角函数
课堂练习:教材P80,1,2
师生活动设计:
练习:教材P81,练习1、2
探究活动:
教材 P83,第9题
锐角 … … …
探究活动:
三、课堂小结
锐角的三角函数值仅仅与该角的大小有关系,如锐角A的正切值,你可以做出一个角大小为A的直角三角形,A的正切值等于A的对边与邻边长度的比值;如果改变该直角三角形的大小,变形后的直角三角形与原来的直角三角形是相似的,所以比值是不变的。
四、布置作业
教材P82,习题28.1,3,4,5,6,7,8
28锐角三角函数
28.1.4锐角三角函数小结
[教学课时]1课时
[教学目标]
1、感知当直角三角形的锐角固定时,它的邻边与斜边、对边与邻边的比值也都固定这一事实;
2、逐步培养学生观察、比较、分析、概括的思维能力。
[教学重点]
理解余弦、正切的概念。
[教学难点]
熟练运用锐角三角函数的概念进行有关计算。
[教学过程]
一、复习回顾
二、巩固提高
例例2
思考:∠EDC转化到
一个直角三角形中,再
根据正切的定义求值。
设左边三角板的最短的边长为1;设右边三角板的一条直角边为1
设左边三角板的最短的边长为1;设右边三角板的一条直角边为1
