青岛版数学九年级上册2.4解直角三角形课件(共25张PPT)
文档属性
| 名称 | 青岛版数学九年级上册2.4解直角三角形课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 740.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 19:36:21 | ||
图片预览








文档简介
(共25张PPT)
2.4解直角三角形
1.了解解直角三角形的含义.
2.经历解直角三角形的过程,掌握解直角三角形的方法.
学习目标
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角比
课时导入
A
B
a
b
c
C
什么是解直角三角形
解直角三角形:
由直角三角形中已知元素求出未知元素的过程,叫作解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
感悟新知
知道五个元素中的几个,就可以求其余元素?
探究
必须已知除直角外的两个元素(至少有一个是边).
已知两边:a.两直角边;b.一直角边和斜边.
已知一边和一锐角:a.一直角边和一锐角;b.斜边和一锐角.
在Rt△ABC中,如果已知其中两边的长,你能求出
这个三角形的其他元
素吗?
类型1
已知两边解直角三角形
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
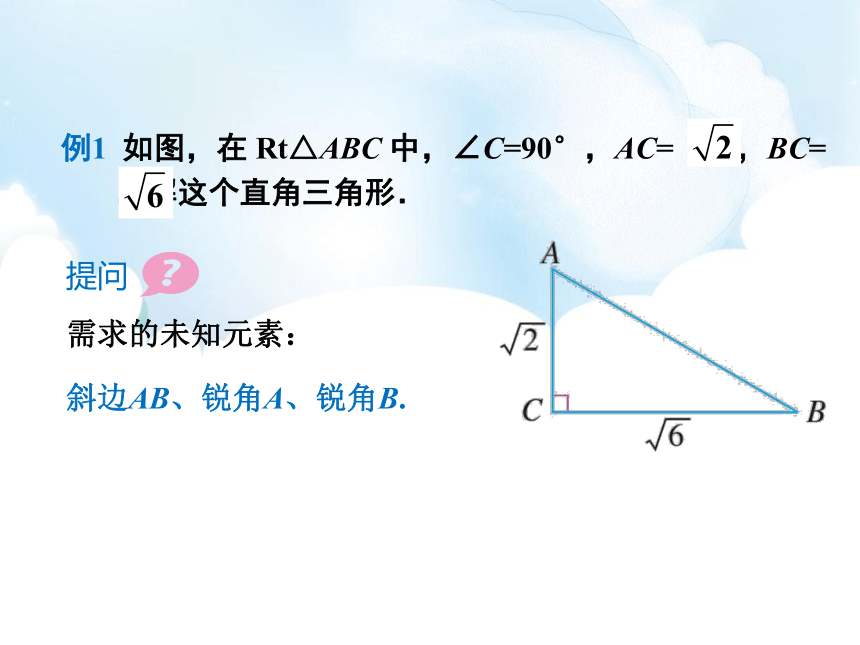
例1
如图,在
Rt△ABC
中,∠C=90°,AC=
,BC=
,解这个直角三角形.
提问
需求的未知元素:
斜边AB、锐角A、锐角B.
方法一:
方法二:
由勾股定理可得AB=
.
例2
已知在Rt△ABC中,∠C=90°,∠A,∠B,∠C
的对边分别为a,b,c,且c=5,b=4,求这个三角
形的其他元素.(角度精确到1′)
求这个直角三角形的其他元素,与“解这个直角三角
形”的含义相同.求角时,可以先求∠A,也可以先
求∠B,因为
=sin
B=cos
A.
导引:
由c=5,b=4,得sin
B=
=0.8,
∴∠B≈53°8′.
∴∠A=90°-∠B≈36°52′.
由勾股定理得
解:
已知直角三角形的一边和一锐角,解直角三角
形时,若已知一直角边a和一锐角A:
①
∠B=90
°-
∠
A;②c=
若已知斜边c和一个锐角A:
①
∠
B=90°-
∠
A;
②a=c·sin
A
;
③b=c·cos
A.
类型2
已知一边及一锐角解直角三角形
例4
如图,在
Rt△ABC中,∠C=90°,∠B=
35°,b=20,解这个直角三角形(结果保留小数点后一位).
提问
需求的未知元素:
直角边a、斜边c、锐角A.
还有别的
解法吗?
总
结
在直角三角形的6个元素中,直角是已知元素,如果
再知道一条边和第三
个元素,那么这个三角形的所有元
素就都可以确定下来.
例5
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分
别为a,b,c,且c=100,∠A=26°44′.求这个三角形
的其他元素.(长度精确到0.01)
已知∠A,可根据∠B=90°-∠A得到∠B的大小.而
已知斜边,必然要用到正弦或余弦函数.
∵∠A=26°44′,∠C=90°,
∴∠B=90°-26°44′=63°16′.
由sin
A=
得a=c·sin
A=100·sin
26°44′≈44.98.
由cos
A=
得b=c·cos
A=100·cos
26°44′≈89.31.
解:
导引:
例6
如图,在△ABC中,AB=1,AC=
sin
B=
求BC的长.
要求的BC边不在直角
三角形中,已知条件中
有∠B的正弦值,作BC边上的高,
将∠B置于直角三角形
中,利用解直角三角形就可
解决问题.
导引:
类型3
已知一边及一锐角的三角比值解直角三角形
如图,过点A作AD⊥BC于点D.
∵AB=1,sin
B=
∴AD=AB·sin
B=1×
=
∴BD=
CD=
∴BC=
解:
总
结
通过作垂线(高),将斜三角形分割成两个直角三角
形,然后利用解直角三角形来解决边或角的问题,这种
“化斜为直”的思想很常见.在作垂线时,要结合已知
条件,充分利用已知条件,如本题若过B点作AC的垂线,
则∠B的正弦值就无法利用.
1.已知在Rt△ABC中,∠C=90°.
(1)若a=
,b=
,则c=
;
(2)若a=10,c=
,则∠B=
;
(3)若b=35,∠A=45°,则a=
;
(4)若c=20,∠A=60°,则a=
.
45°
35
随堂练习
2.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
解:∵△ABD是等边三角形,∴∠B=60°.
在Rt△ABC中,AB=2,∠B=60°,
△ABC的周长为2+
+4=6+
3.在Rt△ABC中,∠C=90°,tanA=
,△ABC
的周长为45cm,CD是斜边AB上的高,求CD的长.(精确到0.1
cm)
5x
12x
13x
解:
5x
12x
13x
解直角三角形
由直角三角形中已知的元素求出未知元素的过程,叫作解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
2.4解直角三角形
1.了解解直角三角形的含义.
2.经历解直角三角形的过程,掌握解直角三角形的方法.
学习目标
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角比
课时导入
A
B
a
b
c
C
什么是解直角三角形
解直角三角形:
由直角三角形中已知元素求出未知元素的过程,叫作解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
感悟新知
知道五个元素中的几个,就可以求其余元素?
探究
必须已知除直角外的两个元素(至少有一个是边).
已知两边:a.两直角边;b.一直角边和斜边.
已知一边和一锐角:a.一直角边和一锐角;b.斜边和一锐角.
在Rt△ABC中,如果已知其中两边的长,你能求出
这个三角形的其他元
素吗?
类型1
已知两边解直角三角形
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
例1
如图,在
Rt△ABC
中,∠C=90°,AC=
,BC=
,解这个直角三角形.
提问
需求的未知元素:
斜边AB、锐角A、锐角B.
方法一:
方法二:
由勾股定理可得AB=
.
例2
已知在Rt△ABC中,∠C=90°,∠A,∠B,∠C
的对边分别为a,b,c,且c=5,b=4,求这个三角
形的其他元素.(角度精确到1′)
求这个直角三角形的其他元素,与“解这个直角三角
形”的含义相同.求角时,可以先求∠A,也可以先
求∠B,因为
=sin
B=cos
A.
导引:
由c=5,b=4,得sin
B=
=0.8,
∴∠B≈53°8′.
∴∠A=90°-∠B≈36°52′.
由勾股定理得
解:
已知直角三角形的一边和一锐角,解直角三角
形时,若已知一直角边a和一锐角A:
①
∠B=90
°-
∠
A;②c=
若已知斜边c和一个锐角A:
①
∠
B=90°-
∠
A;
②a=c·sin
A
;
③b=c·cos
A.
类型2
已知一边及一锐角解直角三角形
例4
如图,在
Rt△ABC中,∠C=90°,∠B=
35°,b=20,解这个直角三角形(结果保留小数点后一位).
提问
需求的未知元素:
直角边a、斜边c、锐角A.
还有别的
解法吗?
总
结
在直角三角形的6个元素中,直角是已知元素,如果
再知道一条边和第三
个元素,那么这个三角形的所有元
素就都可以确定下来.
例5
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分
别为a,b,c,且c=100,∠A=26°44′.求这个三角形
的其他元素.(长度精确到0.01)
已知∠A,可根据∠B=90°-∠A得到∠B的大小.而
已知斜边,必然要用到正弦或余弦函数.
∵∠A=26°44′,∠C=90°,
∴∠B=90°-26°44′=63°16′.
由sin
A=
得a=c·sin
A=100·sin
26°44′≈44.98.
由cos
A=
得b=c·cos
A=100·cos
26°44′≈89.31.
解:
导引:
例6
如图,在△ABC中,AB=1,AC=
sin
B=
求BC的长.
要求的BC边不在直角
三角形中,已知条件中
有∠B的正弦值,作BC边上的高,
将∠B置于直角三角形
中,利用解直角三角形就可
解决问题.
导引:
类型3
已知一边及一锐角的三角比值解直角三角形
如图,过点A作AD⊥BC于点D.
∵AB=1,sin
B=
∴AD=AB·sin
B=1×
=
∴BD=
CD=
∴BC=
解:
总
结
通过作垂线(高),将斜三角形分割成两个直角三角
形,然后利用解直角三角形来解决边或角的问题,这种
“化斜为直”的思想很常见.在作垂线时,要结合已知
条件,充分利用已知条件,如本题若过B点作AC的垂线,
则∠B的正弦值就无法利用.
1.已知在Rt△ABC中,∠C=90°.
(1)若a=
,b=
,则c=
;
(2)若a=10,c=
,则∠B=
;
(3)若b=35,∠A=45°,则a=
;
(4)若c=20,∠A=60°,则a=
.
45°
35
随堂练习
2.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
解:∵△ABD是等边三角形,∴∠B=60°.
在Rt△ABC中,AB=2,∠B=60°,
△ABC的周长为2+
+4=6+
3.在Rt△ABC中,∠C=90°,tanA=
,△ABC
的周长为45cm,CD是斜边AB上的高,求CD的长.(精确到0.1
cm)
5x
12x
13x
解:
5x
12x
13x
解直角三角形
由直角三角形中已知的元素求出未知元素的过程,叫作解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
