人教B版(2019)高中数学选择性必修第一册 2.7.1 抛物线的标准方程word含答案
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 2.7.1 抛物线的标准方程word含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 16:05:03 | ||
图片预览


文档简介
2.7 抛物线及其方程
2.7.1 抛物线的标准方程
课后篇巩固提升
基础达标练
1.(多选)对抛物线x2=4y,下列描述不正确的是( )
A.开口向上,焦点为(0,1)
B.开口向上,焦点为0,116
C.开口向右,焦点为(1,0)
D.开口向右,焦点为116,0
解析∵抛物线的标准方程为x2=4y,
∴2p=4,p=2,解得p2=1,因此抛物线的焦点为(0,1),准线为y=-1,可得该抛物线的开口向上.
答案BCD
2.抛物线y=2x2的焦点到准线的距离是( )
A.2 B.1 C.14 D.12
解析抛物线y=2x2化为x2=12y,
∴焦点到准线的距离为14.
答案C
3.平面上动点M到点F(3,0)的距离等于M到直线l:x=-3的距离,则动点M满足的方程是( )
A.y2=6x B.y2=12x
C.x2=6y D.x2=12y
解析由条件可知,点M到点F(3,0)的距离与到直线x=-3的距离相等,所以点M的轨迹是以F(3,0)为焦点,x=-3为准线的抛物线,其方程为y2=12x.
答案B
4.已知抛物线y2=2px(p>0)的准线经过点(-1,1),则该抛物线焦点坐标为( )
A.(-1,0) B.(1,0)
C.(0,-1) D.(0,1)
解析抛物线y2=2px(p>0)的准线方程为x=-p2,由题设知-p2=-1,即p=2,故焦点坐标为(1,0).
答案B
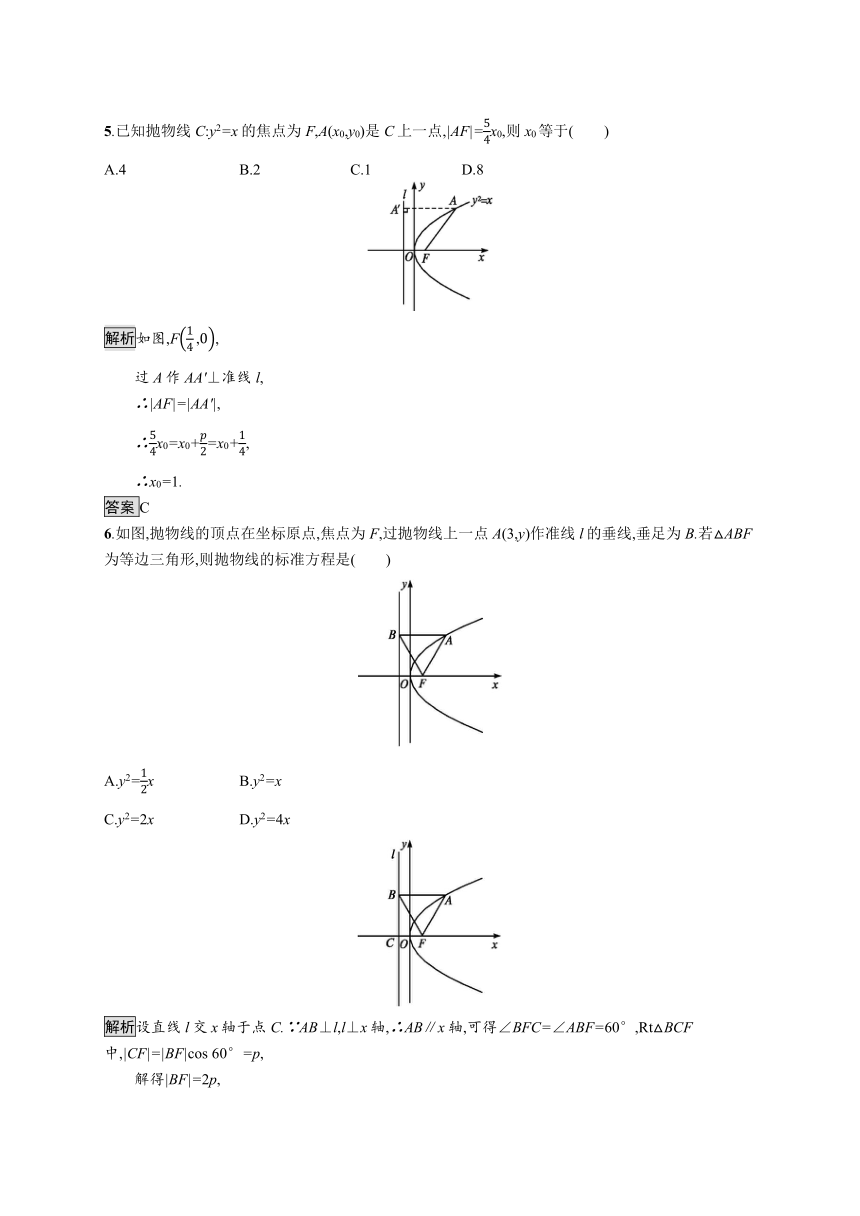
5.已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=54x0,则x0等于( )
A.4 B.2 C.1 D.8
解析如图,F14,0,
过A作AA'⊥准线l,
∴|AF|=|AA'|,
∴54x0=x0+p2=x0+14,
∴x0=1.
答案C
6.如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l的垂线,垂足为B.若△ABF为等边三角形,则抛物线的标准方程是( )
A.y2=12x B.y2=x
C.y2=2x D.y2=4x
解析设直线l交x轴于点C.∵AB⊥l,l⊥x轴,∴AB∥x轴,可得∠BFC=∠ABF=60°,Rt△BCF中,|CF|=|BF|cos 60°=p,
解得|BF|=2p,
由AB⊥y轴,可得3+p2=2p,∴p=2,∴抛物线的标准方程是y2=4x.
答案D
7.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是 .?
解析抛物线y2=4x的焦点F(1,0),准线为x=-1.由M到焦点的距离为10,可知M到准线x=-1的距离也为10,故M的横坐标满足xM+1=10,解得xM=9,所以点M到y轴的距离为9.
答案9
8.一抛物线形拱桥,当桥顶离水面2米时,水面宽4米,若水面下降2米,则水面宽为 米.?
解析以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,建立如图所示的平面直角坐标系,设抛物线方程为x2=-2py(p>0).
由当桥顶离水面2米时,水面宽4米可得图中点A的坐标为(2,-2),
所以4=-2p×(-2),解得p=1.
所以抛物线的方程为x2=-2y.
当水面下降2米,即当y=-4时,
可得x2=-2×(-4)=8,解得x=±22,
因此水面宽为42米.
答案42
9.根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解(1)双曲线方程可化为x29-y216=1,左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0)且-p2=-3,∴p=6,∴抛物线的方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为y2=2nx(n≠0),A(m,-3),
由抛物线定义得5=|AF|=m+n2.
又(-3)2=2nm,∴n=±1或n=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
10.已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A的坐标是(8,7),求|PA|+|PQ|的最小值.
解抛物线的焦点为F(0,1),准线方程为y=-1,
如图,设点P在准线上的射影是点M,
根据抛物线的定义知,|PF|=|PM|=|PQ|+1.
所以|PA|+|PQ|=|PA|+|PM|-1=|PA|+|PF|-1≥|AF|-1=82+(7-1)2-1=10-1=9,
当且仅当A,P,F三点共线时,等号成立.
故|PA|+|PQ|的最小值为9.
能力提升练
1.AB是抛物线y2=2x的一条焦点弦,|AB|=4,则AB中点C的横坐标是( )
A.2 B.12 C.32 D.52
解析设A(x1,y1),B(x2,y2),
根据抛物线的定义可知,|AB|=x1+x2+p=x1+x2+1=4,∴x1+x22=32.
答案C
2.抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若|AF|,|BF|,|CF|成等差数列,则( )
A.x1,x2,x3成等差数列 B.x1,x3,x2成等差数列
C.y1,y2,y3成等差数列 D.y1,y3,y2成等差数列
解析∵抛物线y2=2px(p>0),
∴其准线方程为x=-p2,
设点A,B,C在直线x=-p2上的射影分别为M,N,Q,由抛物线的定义得|AF|=|AM|=x1+p2,|BF|=|BN|=x2+p2,|CF|=|CQ|=x3+p2,
∵|AF|,|BF|,|CF|成等差数列,
∴2|BF|=|AF|+|CF|,
∴2x2+p2=x1+p2+x3+p2,∴2x2=x1+x3,
∴x1,x2,x3成等差数列.
答案A
3.(多选)方程(x-2)2+(y-2)2=|3x-4y-6|5表示的曲线不可能为( )
A.抛物线 B.椭圆
C.双曲线 D.圆
解析设P(x,y),由方程(x-2)2+(y-2)2=|3x-4y-6|5得,点P到点F(2,2)的距离等于点P到直线3x-4y-6=0的距离,又点F不在直线3x-4y-6=0上,由抛物线的定义得,曲线为抛物线.
答案BCD
4.以下四个命题:
①平面内与一定点F和一条定直线l的距离相等的点的轨迹是抛物线;
②抛物线y=ax2的焦点到原点的距离是|a|4;
③直线l与抛物线y2=2px(p>0)交于两点A(x1,y1),B(x2,y2),则|AB|=x1+x2+p;
④正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,则此正三角形的边长为43p.
其中正确命题的序号是 .?
解析①当定点F正好在定直线l上时,平面内与一定点F和一条定直线l的距离相等的点的轨迹不是抛物线,故①错;
②当a>0时,整理抛物线方程得x2=1ay,p=12a.
所以焦点坐标为0,14a,抛物线y=ax2的焦点到原点的距离是14|a|,故②错;
③当直线l不是过抛物线焦点的直线时,直线l与抛物线y2=2px(p>0)交于两点A(x1,y1),B(x2,y2),则|AB|=x1+x2+p不成立,故③错;
④设正三角形另外两个顶点的坐标分别为m22p,m,m22p,-m,由tan 30°=33=mm22p,
解得 m=23p,故这个正三角形的边长为2m=43p,故④正确.
答案④
5.已知曲线C上的任意一点到定点F(1,0)的距离与到定直线x=-1的距离相等.
(1)求曲线C的方程;
(2)若曲线C上有两个定点A,B分别在其对称轴的上、下两侧,且|FA|=2,|FB|=5,求原点O到直线AB的距离.
解(1)∵曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等,
∴曲线C的轨迹是以F(1,0)为焦点的抛物线,且p2=1,∴曲线C的方程为y2=4x.
(2)由抛物线的定义结合|FA|=2可得,A到准线x=-1的距离为2,
即A的横坐标为1,代入抛物线方程可得y=2,即A(1,2),同理可得B(4,-4),故直线AB的斜率k=2-(-4)1-4=-2,
故AB的方程为y-2=-2(x-1),
即2x+y-4=0,由点到直线的距离公式可得,原点O到直线AB的距离为|-4|22+12=455.
素养培优练
1.如图,正方体ABCD-A1B1C1D1的棱长为3,点M在AB上,且|AM|=13|AB|,点P在平面ABCD上,且动点P到直线A1D1的距离与P到点M的距离相等,在平面直角坐标系xAy中,动点P的轨迹方程是 ,此曲线的焦点为 .?
解析作PN⊥AD,NH⊥A1D1,N,H为垂足,图略,则PN⊥面A1D1DA,
由线面垂直的判定可得出 PH⊥A1D1.
以AD,AB,AA1 为x轴,y轴,z轴,建立空间直角坐标系,设P(x,y,0),由题意可得 M(0,1,0),H(x,0,3),|PM|=|PH|,∴x2+(y-1)2=y2+9,
整理,得x2=2y+8,即x2=2(y+4),∴该曲线的焦点可以看作是由x2=2y的焦点向下平移4个单位长度得到的,即0,-72.
答案x2=2y+8 0,-72
2.已知M到点F(1,0)和直线x=-1的距离相等,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)过点F作相互垂直的两条直线l1,l2,曲线C与l1交于点P1,P2,与l2交于点Q1,Q2,试证明:1|P1P2|+1|Q1Q2|=14.
(1)解∵点M到点F(1,0)和直线x=-1的距离相等,
由抛物线的定义可知,点M的轨迹是抛物线,
设方程为y2=2px(p>0),
∵p2=1,∴p=2.
∴轨迹C的方程为y2=4x.
(2)证明由题意知,l1,l2的斜率均存在且不为0.
设l1的方程为y=k(x-1),代入抛物线方程,
整理可得k2x-(2k2+4)x+k2=0,
设P1,P2的横坐标分别为x1,x2,
则x1+x2=2k2+4k2,
∴|P1P2|=x1+x2+p=4k2+4k2,
以-1k代入,可得|Q1Q2|=4+4k2,
∴1|P1P2|+1|Q1Q2|=14.
2.7.1 抛物线的标准方程
课后篇巩固提升
基础达标练
1.(多选)对抛物线x2=4y,下列描述不正确的是( )
A.开口向上,焦点为(0,1)
B.开口向上,焦点为0,116
C.开口向右,焦点为(1,0)
D.开口向右,焦点为116,0
解析∵抛物线的标准方程为x2=4y,
∴2p=4,p=2,解得p2=1,因此抛物线的焦点为(0,1),准线为y=-1,可得该抛物线的开口向上.
答案BCD
2.抛物线y=2x2的焦点到准线的距离是( )
A.2 B.1 C.14 D.12
解析抛物线y=2x2化为x2=12y,
∴焦点到准线的距离为14.
答案C
3.平面上动点M到点F(3,0)的距离等于M到直线l:x=-3的距离,则动点M满足的方程是( )
A.y2=6x B.y2=12x
C.x2=6y D.x2=12y
解析由条件可知,点M到点F(3,0)的距离与到直线x=-3的距离相等,所以点M的轨迹是以F(3,0)为焦点,x=-3为准线的抛物线,其方程为y2=12x.
答案B
4.已知抛物线y2=2px(p>0)的准线经过点(-1,1),则该抛物线焦点坐标为( )
A.(-1,0) B.(1,0)
C.(0,-1) D.(0,1)
解析抛物线y2=2px(p>0)的准线方程为x=-p2,由题设知-p2=-1,即p=2,故焦点坐标为(1,0).
答案B
5.已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=54x0,则x0等于( )
A.4 B.2 C.1 D.8
解析如图,F14,0,
过A作AA'⊥准线l,
∴|AF|=|AA'|,
∴54x0=x0+p2=x0+14,
∴x0=1.
答案C
6.如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l的垂线,垂足为B.若△ABF为等边三角形,则抛物线的标准方程是( )
A.y2=12x B.y2=x
C.y2=2x D.y2=4x
解析设直线l交x轴于点C.∵AB⊥l,l⊥x轴,∴AB∥x轴,可得∠BFC=∠ABF=60°,Rt△BCF中,|CF|=|BF|cos 60°=p,
解得|BF|=2p,
由AB⊥y轴,可得3+p2=2p,∴p=2,∴抛物线的标准方程是y2=4x.
答案D
7.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是 .?
解析抛物线y2=4x的焦点F(1,0),准线为x=-1.由M到焦点的距离为10,可知M到准线x=-1的距离也为10,故M的横坐标满足xM+1=10,解得xM=9,所以点M到y轴的距离为9.
答案9
8.一抛物线形拱桥,当桥顶离水面2米时,水面宽4米,若水面下降2米,则水面宽为 米.?
解析以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,建立如图所示的平面直角坐标系,设抛物线方程为x2=-2py(p>0).
由当桥顶离水面2米时,水面宽4米可得图中点A的坐标为(2,-2),
所以4=-2p×(-2),解得p=1.
所以抛物线的方程为x2=-2y.
当水面下降2米,即当y=-4时,
可得x2=-2×(-4)=8,解得x=±22,
因此水面宽为42米.
答案42
9.根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解(1)双曲线方程可化为x29-y216=1,左顶点为(-3,0),
由题意设抛物线方程为y2=-2px(p>0)且-p2=-3,∴p=6,∴抛物线的方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为y2=2nx(n≠0),A(m,-3),
由抛物线定义得5=|AF|=m+n2.
又(-3)2=2nm,∴n=±1或n=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
10.已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A的坐标是(8,7),求|PA|+|PQ|的最小值.
解抛物线的焦点为F(0,1),准线方程为y=-1,
如图,设点P在准线上的射影是点M,
根据抛物线的定义知,|PF|=|PM|=|PQ|+1.
所以|PA|+|PQ|=|PA|+|PM|-1=|PA|+|PF|-1≥|AF|-1=82+(7-1)2-1=10-1=9,
当且仅当A,P,F三点共线时,等号成立.
故|PA|+|PQ|的最小值为9.
能力提升练
1.AB是抛物线y2=2x的一条焦点弦,|AB|=4,则AB中点C的横坐标是( )
A.2 B.12 C.32 D.52
解析设A(x1,y1),B(x2,y2),
根据抛物线的定义可知,|AB|=x1+x2+p=x1+x2+1=4,∴x1+x22=32.
答案C
2.抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若|AF|,|BF|,|CF|成等差数列,则( )
A.x1,x2,x3成等差数列 B.x1,x3,x2成等差数列
C.y1,y2,y3成等差数列 D.y1,y3,y2成等差数列
解析∵抛物线y2=2px(p>0),
∴其准线方程为x=-p2,
设点A,B,C在直线x=-p2上的射影分别为M,N,Q,由抛物线的定义得|AF|=|AM|=x1+p2,|BF|=|BN|=x2+p2,|CF|=|CQ|=x3+p2,
∵|AF|,|BF|,|CF|成等差数列,
∴2|BF|=|AF|+|CF|,
∴2x2+p2=x1+p2+x3+p2,∴2x2=x1+x3,
∴x1,x2,x3成等差数列.
答案A
3.(多选)方程(x-2)2+(y-2)2=|3x-4y-6|5表示的曲线不可能为( )
A.抛物线 B.椭圆
C.双曲线 D.圆
解析设P(x,y),由方程(x-2)2+(y-2)2=|3x-4y-6|5得,点P到点F(2,2)的距离等于点P到直线3x-4y-6=0的距离,又点F不在直线3x-4y-6=0上,由抛物线的定义得,曲线为抛物线.
答案BCD
4.以下四个命题:
①平面内与一定点F和一条定直线l的距离相等的点的轨迹是抛物线;
②抛物线y=ax2的焦点到原点的距离是|a|4;
③直线l与抛物线y2=2px(p>0)交于两点A(x1,y1),B(x2,y2),则|AB|=x1+x2+p;
④正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,则此正三角形的边长为43p.
其中正确命题的序号是 .?
解析①当定点F正好在定直线l上时,平面内与一定点F和一条定直线l的距离相等的点的轨迹不是抛物线,故①错;
②当a>0时,整理抛物线方程得x2=1ay,p=12a.
所以焦点坐标为0,14a,抛物线y=ax2的焦点到原点的距离是14|a|,故②错;
③当直线l不是过抛物线焦点的直线时,直线l与抛物线y2=2px(p>0)交于两点A(x1,y1),B(x2,y2),则|AB|=x1+x2+p不成立,故③错;
④设正三角形另外两个顶点的坐标分别为m22p,m,m22p,-m,由tan 30°=33=mm22p,
解得 m=23p,故这个正三角形的边长为2m=43p,故④正确.
答案④
5.已知曲线C上的任意一点到定点F(1,0)的距离与到定直线x=-1的距离相等.
(1)求曲线C的方程;
(2)若曲线C上有两个定点A,B分别在其对称轴的上、下两侧,且|FA|=2,|FB|=5,求原点O到直线AB的距离.
解(1)∵曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等,
∴曲线C的轨迹是以F(1,0)为焦点的抛物线,且p2=1,∴曲线C的方程为y2=4x.
(2)由抛物线的定义结合|FA|=2可得,A到准线x=-1的距离为2,
即A的横坐标为1,代入抛物线方程可得y=2,即A(1,2),同理可得B(4,-4),故直线AB的斜率k=2-(-4)1-4=-2,
故AB的方程为y-2=-2(x-1),
即2x+y-4=0,由点到直线的距离公式可得,原点O到直线AB的距离为|-4|22+12=455.
素养培优练
1.如图,正方体ABCD-A1B1C1D1的棱长为3,点M在AB上,且|AM|=13|AB|,点P在平面ABCD上,且动点P到直线A1D1的距离与P到点M的距离相等,在平面直角坐标系xAy中,动点P的轨迹方程是 ,此曲线的焦点为 .?
解析作PN⊥AD,NH⊥A1D1,N,H为垂足,图略,则PN⊥面A1D1DA,
由线面垂直的判定可得出 PH⊥A1D1.
以AD,AB,AA1 为x轴,y轴,z轴,建立空间直角坐标系,设P(x,y,0),由题意可得 M(0,1,0),H(x,0,3),|PM|=|PH|,∴x2+(y-1)2=y2+9,
整理,得x2=2y+8,即x2=2(y+4),∴该曲线的焦点可以看作是由x2=2y的焦点向下平移4个单位长度得到的,即0,-72.
答案x2=2y+8 0,-72
2.已知M到点F(1,0)和直线x=-1的距离相等,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)过点F作相互垂直的两条直线l1,l2,曲线C与l1交于点P1,P2,与l2交于点Q1,Q2,试证明:1|P1P2|+1|Q1Q2|=14.
(1)解∵点M到点F(1,0)和直线x=-1的距离相等,
由抛物线的定义可知,点M的轨迹是抛物线,
设方程为y2=2px(p>0),
∵p2=1,∴p=2.
∴轨迹C的方程为y2=4x.
(2)证明由题意知,l1,l2的斜率均存在且不为0.
设l1的方程为y=k(x-1),代入抛物线方程,
整理可得k2x-(2k2+4)x+k2=0,
设P1,P2的横坐标分别为x1,x2,
则x1+x2=2k2+4k2,
∴|P1P2|=x1+x2+p=4k2+4k2,
以-1k代入,可得|Q1Q2|=4+4k2,
∴1|P1P2|+1|Q1Q2|=14.
