因式分解法解一元一次方程
文档属性
| 名称 | 因式分解法解一元一次方程 |  | |
| 格式 | rar | ||
| 文件大小 | 190.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-20 13:30:56 | ||
图片预览







文档简介
(共21张PPT)
人教版九年级上册
因式分解法解一元二次方程
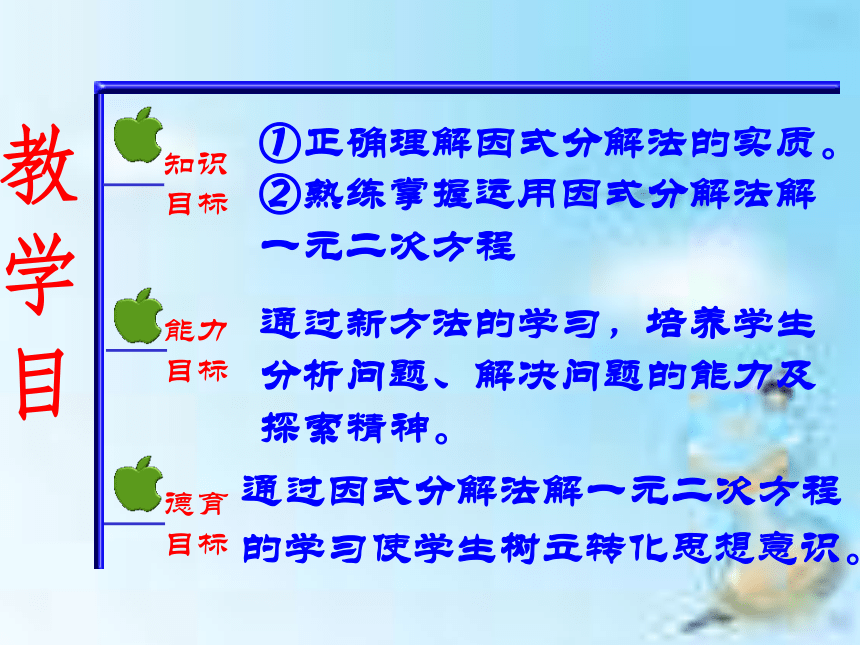
①正确理解因式分解法的实质。
②熟练掌握运用因式分解法解一元二次方程
通过新方法的学习,培养学生分析问题、解决问题的能力及探索精神。
通过因式分解法解一元二次方程的学习使学生树立转化思想意识。
知识
目标
能力
目标
德育
目标
教学目标
教学重点和难点
重点:
因式分解法解一元二次方程。
难点:
将一元二次方程转化为“A=0或B=0”的形式。(A、B为两个一次因式)。
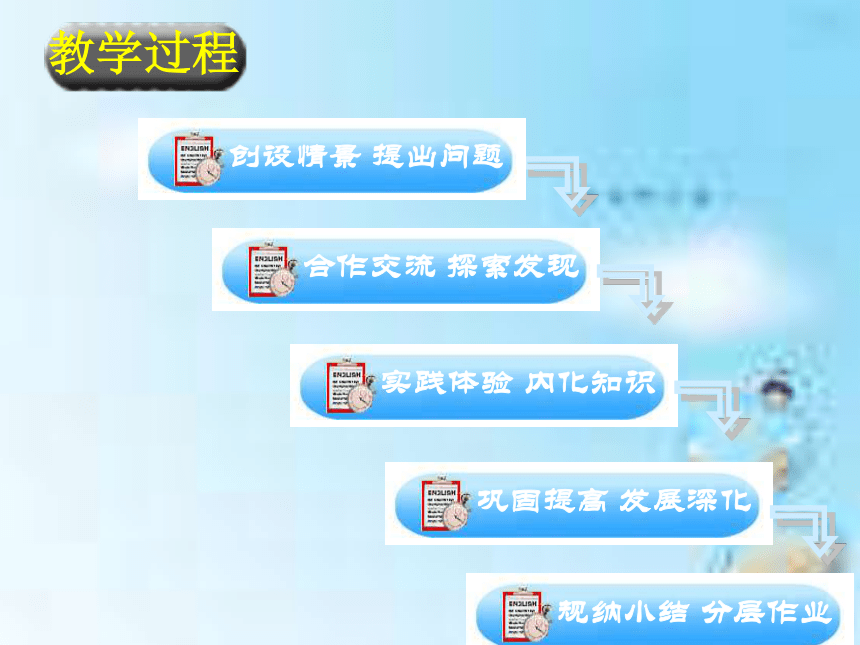
采用“问题式教学法”“类比法”的思想进行教学设计,分五个基本环节:创设情景、提出问题——合作交流、探究发现——实践体验、内化知识——巩固提高,发展深化——归纳小结,分层作业。
教学方法
教学过程
实践体验 内化知识
巩固提高 发展深化
合作交流 探索发现
规纳小结 分层作业
创设情景 提出问题
问题情境一:
根据物理学规律,如果把一个物体从地面以10m/s的速度竖直上抛,那么经过x秒物体离地面的高度(单位:m)为 10x-4.9x2 你能跟据上述规律求出物体经过多少秒落回地面吗?(精确到0.01s)
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
问题情境二
一个数的平方与这个数的3倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?小颖,小亮都设这个数为x,根据题意得
小颖是这样解的: 小亮是这样解的:
解: 解:方程 两边同除以x得
所以 x=3
所以 x=0或x=3 所以这个数是3
所以这个数是0 或3
小颖做得对吗? 小亮做得对吗?
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3X+5=0 或 3x-5=0
9X2-25= (3x+5)(3x-5)
因式分解法的条件是方程左边易于分解,而右边等于零,关键是熟练掌握因式分解的知识,理论依旧是"如果两个因式的积等于零,那么至少有一个因式等于零”.
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
因式分解法解一元二次方程的步骤是:
①化方程为一般形式;
②将方程左边因式分解;
③至少有一个因式为零,得到两个一元一次方程;
④两个一元一次方程的解就是原方程的解.
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
归纳新知,形成技巧
解题框架图
解:原方程可变形为:
=0
(一次因式A )(一次因式B )=0
一次因式A =0或一次因式B =0
∴ x1= A解 , x2= B解
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
右化零 左分解
两因式 各求解
简记歌诀:
解下列一元二次方程:
(1) x(x-2)+x-2=0
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
完成课本P 45 练习题1
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
用因式分解法解下列方程:
(1)x2-4x=0
(2) x2 +7x+12=0
(3)(x-5)(x+2)=18
(6) x(x-1)(x+1)=0
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
本节课你最大的体验是什么?
本节课你学习了哪些知识?
回
顾
与
思
考
本节课你掌握了哪些数学方法?
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
必做:1.p46: 第5题,
2.p46: 第8题,
选做:对正实数a 、b作定义
若4*x=20 ,求x值。
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
课题:因式分解法解一元二次方程
因式分解法解一元二次 例:……
方程的步骤 解:……
光 …
荣 …
榜 …
板书设计
人教版九年级上册
因式分解法解一元二次方程
①正确理解因式分解法的实质。
②熟练掌握运用因式分解法解一元二次方程
通过新方法的学习,培养学生分析问题、解决问题的能力及探索精神。
通过因式分解法解一元二次方程的学习使学生树立转化思想意识。
知识
目标
能力
目标
德育
目标
教学目标
教学重点和难点
重点:
因式分解法解一元二次方程。
难点:
将一元二次方程转化为“A=0或B=0”的形式。(A、B为两个一次因式)。
采用“问题式教学法”“类比法”的思想进行教学设计,分五个基本环节:创设情景、提出问题——合作交流、探究发现——实践体验、内化知识——巩固提高,发展深化——归纳小结,分层作业。
教学方法
教学过程
实践体验 内化知识
巩固提高 发展深化
合作交流 探索发现
规纳小结 分层作业
创设情景 提出问题
问题情境一:
根据物理学规律,如果把一个物体从地面以10m/s的速度竖直上抛,那么经过x秒物体离地面的高度(单位:m)为 10x-4.9x2 你能跟据上述规律求出物体经过多少秒落回地面吗?(精确到0.01s)
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
问题情境二
一个数的平方与这个数的3倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?小颖,小亮都设这个数为x,根据题意得
小颖是这样解的: 小亮是这样解的:
解: 解:方程 两边同除以x得
所以 x=3
所以 x=0或x=3 所以这个数是3
所以这个数是0 或3
小颖做得对吗? 小亮做得对吗?
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
解法一
(直接开平方法):
9x2-25=0
解:原方程可变形为
(3x+5)(3x-5)=0
3X+5=0 或 3x-5=0
9X2-25= (3x+5)(3x-5)
因式分解法的条件是方程左边易于分解,而右边等于零,关键是熟练掌握因式分解的知识,理论依旧是"如果两个因式的积等于零,那么至少有一个因式等于零”.
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
因式分解法解一元二次方程的步骤是:
①化方程为一般形式;
②将方程左边因式分解;
③至少有一个因式为零,得到两个一元一次方程;
④两个一元一次方程的解就是原方程的解.
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
归纳新知,形成技巧
解题框架图
解:原方程可变形为:
=0
(一次因式A )(一次因式B )=0
一次因式A =0或一次因式B =0
∴ x1= A解 , x2= B解
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
右化零 左分解
两因式 各求解
简记歌诀:
解下列一元二次方程:
(1) x(x-2)+x-2=0
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
完成课本P 45 练习题1
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
用因式分解法解下列方程:
(1)x2-4x=0
(2) x2 +7x+12=0
(3)(x-5)(x+2)=18
(6) x(x-1)(x+1)=0
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
本节课你最大的体验是什么?
本节课你学习了哪些知识?
回
顾
与
思
考
本节课你掌握了哪些数学方法?
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
必做:1.p46: 第5题,
2.p46: 第8题,
选做:对正实数a 、b作定义
若4*x=20 ,求x值。
巩固提高
发展深化
规纳小结
分层作业
实践体验
内化知识
创设情景
提出问题
合作交流
探索发现
课题:因式分解法解一元二次方程
因式分解法解一元二次 例:……
方程的步骤 解:……
光 …
荣 …
榜 …
板书设计
同课章节目录
