1.4.1 有理数的乘法(1)课件(共21张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法(1)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 14:58:00 | ||
图片预览




文档简介
(共21张PPT)
人教版
七年级上
1.4.1有理数的乘法(1)
学习目标
1.理解并掌握多个有理数相乘时积的符号的确定,能利用乘法运算律进行简便计算
2.理解并掌握有理数乘法的交换律,结合律和分配律,并能灵活运用乘法运算律进行有理数的乘法运算,使之计算简便。
3.理解乘法运算律在乘法运算中的作用,适当进行推理训练。
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现
3×(-3),(-3)×3(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
这就是我们本节课要学习的内容
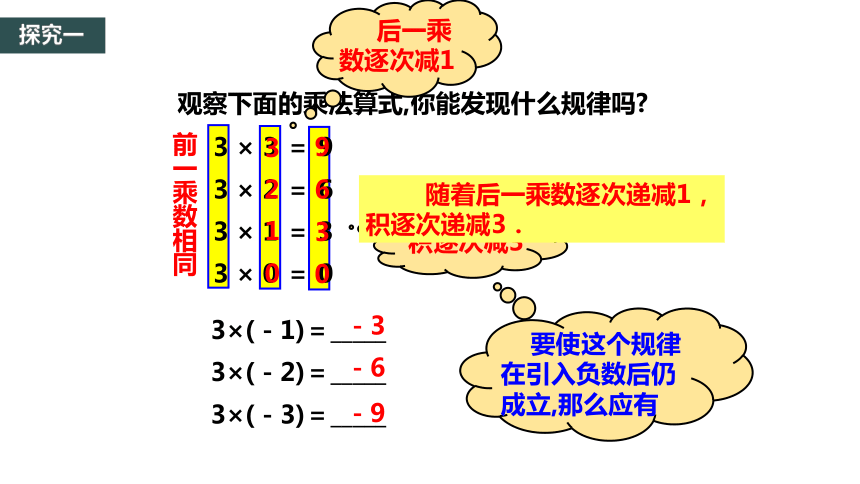
观察下面的乘法算式,你能发现什么规律吗?
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
9
6
3
0
3
2
1
0
前一乘数相同
后一乘数逐次减1
积逐次减3
3×(-1)=_____
3×(-2)=_____
3×(-3)=_____
-3
-6
-9
随着后一乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍成立,那么应有
探究一
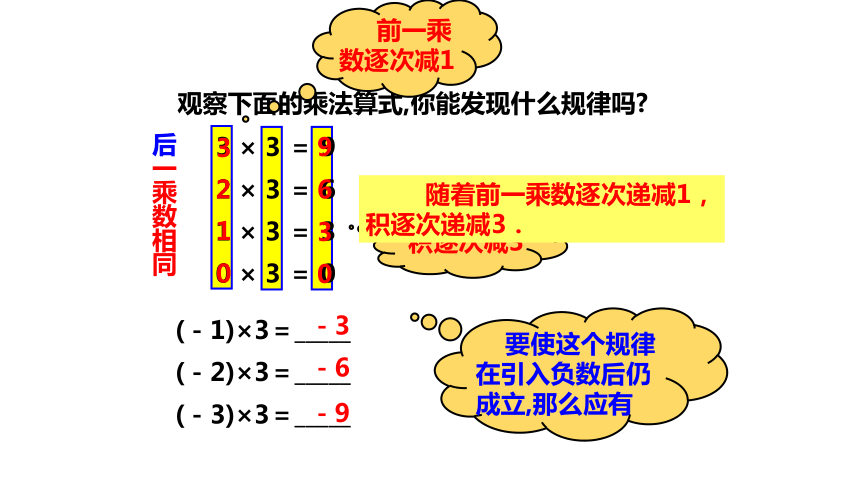
观察下面的乘法算式,你能发现什么规律吗?
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
9
6
3
0
3
2
1
0
后一乘数相同
前一乘数逐次减1
积逐次减3
(-1)×3=_____
(-2)×3=_____
(-3)×3=_____
-3
-6
-9
随着前一乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍成立,那么应有
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
3×(-1)=-3
3×(-2)=-6
3×(-3)=-9
(-1)×3
=-3
(-2)×3
=-6
(-3)×3
=-9
积的绝对值等于各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,负数乘正数,积为负数;
观察下面算式:
从符号和绝对值两个角度,说一说你有什么发现?
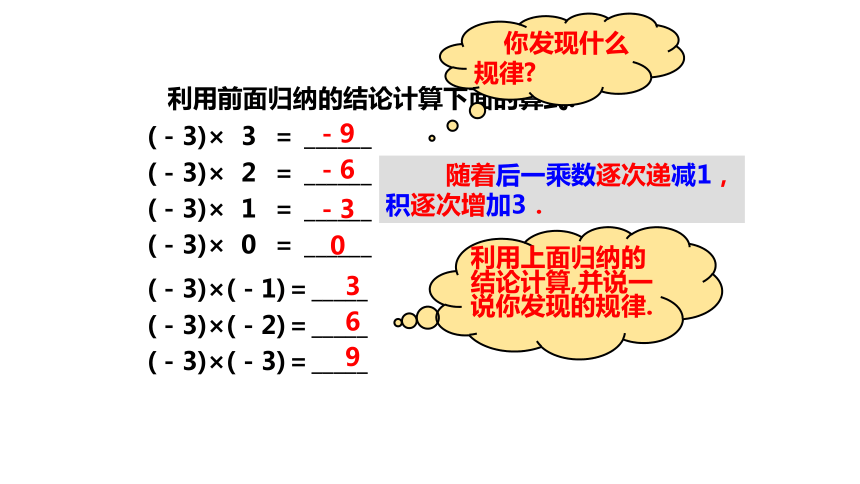
利用前面归纳的结论计算下面的算式:
(-3)×
3
=
______
(-3)×
2
=
______
(-3)×
1
=
______
(-3)×
0
=
______
-9
-6
-3
0
你发现什么规律?
随着后一乘数逐次递减1,积逐次增加3.
(-3)×(-1)=_____
(-3)×(-2)=_____
(-3)×(-3)=_____
3
6
9
利用上面归纳的结论计算,并说一说你发现的规律.
正数乘正数积为(
)数
负数乘正数积为(
)数
正数乘负数积为(
)数
负数乘负数的积(
)数
乘积的绝对值等于各乘数绝对值的(
)
正
负
负
正
积
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
任何数与1相乘都等于它本身,任何数与-1相乘都等于它的相反数.
例题讲解
例1
计算:
(1)
(-3)×9;
(2)
8×(-1);
解:
(1)
(-3)×9=-27;
(2)
8×(-1)
=-8;
要得到一个数的相反数,只要将它乘
-1.
定义:有理数中,乘积是1的两个数互为倒数.
例2:用正负数表示气温的变化量,上升为正,下降为负,登山队攀登一座山峰,每登高1
km气温的变化量为-6
?C,攀登3
km后,气温有什么变化?
解:
(-6)×3=-18
答:气温下降18
℃.
例题讲解
要点1 有理数的乘法法则
1.
两数相乘,同号得
,异号得
,并把
相乘.
2.
任何数同0相乘,都得
;任何数与1相乘都等于它
;任何数与-1相乘都等于它的
.
?
要点2 倒数
1.
乘积是
的两个数互为倒数.
2.
0没有倒数;1或-1的倒数是它
;倒数是相互的,当ab=
时,a叫做b的倒数,b也叫做a的倒数.
课堂练习
正
负
绝对值
0
本身
相反数
1
本身
1
1.下列说法正确的是( )
①两个正数中倒数大的反而小;②两个负数中倒数大的反而小;③两个有理数中倒数大的反而小;④两个符号相同的有理数中倒数大的反而小.
A.
①②④
B.
①
C.
①②③
D.
①④
A
2.下列计算正确的有(
)
①(-3)×(-4)=-12;②(-2)×5=-10;③(-41)×(-1)=-41;
④24×(-5)=120.
A.1个
B.2个
C.3个
D.4个
A
3.计算:
4.已知有理数m,n在数轴上的对应点的位置如图所示,则下列判断正确的是.
A.m>0
B.n<0
C.mn<0
D.m-n>0
C
5.填空:
-7的倒数是
,-0.6的倒数是
,
的倒数是
.
?
6.已知|a|=2,|b|=2,求ab的值.
6.
解:因为|a|=2,|b|=2,所以a=±2,b=±2.(1)当a=b=2时,ab=2×2=4;
(2)当a=2,b=-2时,ab=2×(-2)=-4;
(3)当a=-2,b=2时,ab=(-2)×2=-4;
(4)当a=-2,b=-2时,ab=(-2)×(-2)=4.
课堂总结
有理数的乘法
有理数的乘法法则
倒数
有理数的乘法的实际运用
2.任何数同0相乘,都得0.
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
有理数中,乘积是1的两个数互为倒数.
教材P30练习题1—3题.
课后作业
谢
谢
观
看
人教版
七年级上
1.4.1有理数的乘法(1)
学习目标
1.理解并掌握多个有理数相乘时积的符号的确定,能利用乘法运算律进行简便计算
2.理解并掌握有理数乘法的交换律,结合律和分配律,并能灵活运用乘法运算律进行有理数的乘法运算,使之计算简便。
3.理解乘法运算律在乘法运算中的作用,适当进行推理训练。
我们已经熟悉正数及0的乘法运算.与加法类似,引入负数后,将出现
3×(-3),(-3)×3(-3)×(-3)这样的乘法.该怎样进行这一类的运算呢?
这就是我们本节课要学习的内容
观察下面的乘法算式,你能发现什么规律吗?
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
9
6
3
0
3
2
1
0
前一乘数相同
后一乘数逐次减1
积逐次减3
3×(-1)=_____
3×(-2)=_____
3×(-3)=_____
-3
-6
-9
随着后一乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍成立,那么应有
探究一
观察下面的乘法算式,你能发现什么规律吗?
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
9
6
3
0
3
2
1
0
后一乘数相同
前一乘数逐次减1
积逐次减3
(-1)×3=_____
(-2)×3=_____
(-3)×3=_____
-3
-6
-9
随着前一乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍成立,那么应有
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
3×(-1)=-3
3×(-2)=-6
3×(-3)=-9
(-1)×3
=-3
(-2)×3
=-6
(-3)×3
=-9
积的绝对值等于各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,负数乘正数,积为负数;
观察下面算式:
从符号和绝对值两个角度,说一说你有什么发现?
利用前面归纳的结论计算下面的算式:
(-3)×
3
=
______
(-3)×
2
=
______
(-3)×
1
=
______
(-3)×
0
=
______
-9
-6
-3
0
你发现什么规律?
随着后一乘数逐次递减1,积逐次增加3.
(-3)×(-1)=_____
(-3)×(-2)=_____
(-3)×(-3)=_____
3
6
9
利用上面归纳的结论计算,并说一说你发现的规律.
正数乘正数积为(
)数
负数乘正数积为(
)数
正数乘负数积为(
)数
负数乘负数的积(
)数
乘积的绝对值等于各乘数绝对值的(
)
正
负
负
正
积
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
任何数与1相乘都等于它本身,任何数与-1相乘都等于它的相反数.
例题讲解
例1
计算:
(1)
(-3)×9;
(2)
8×(-1);
解:
(1)
(-3)×9=-27;
(2)
8×(-1)
=-8;
要得到一个数的相反数,只要将它乘
-1.
定义:有理数中,乘积是1的两个数互为倒数.
例2:用正负数表示气温的变化量,上升为正,下降为负,登山队攀登一座山峰,每登高1
km气温的变化量为-6
?C,攀登3
km后,气温有什么变化?
解:
(-6)×3=-18
答:气温下降18
℃.
例题讲解
要点1 有理数的乘法法则
1.
两数相乘,同号得
,异号得
,并把
相乘.
2.
任何数同0相乘,都得
;任何数与1相乘都等于它
;任何数与-1相乘都等于它的
.
?
要点2 倒数
1.
乘积是
的两个数互为倒数.
2.
0没有倒数;1或-1的倒数是它
;倒数是相互的,当ab=
时,a叫做b的倒数,b也叫做a的倒数.
课堂练习
正
负
绝对值
0
本身
相反数
1
本身
1
1.下列说法正确的是( )
①两个正数中倒数大的反而小;②两个负数中倒数大的反而小;③两个有理数中倒数大的反而小;④两个符号相同的有理数中倒数大的反而小.
A.
①②④
B.
①
C.
①②③
D.
①④
A
2.下列计算正确的有(
)
①(-3)×(-4)=-12;②(-2)×5=-10;③(-41)×(-1)=-41;
④24×(-5)=120.
A.1个
B.2个
C.3个
D.4个
A
3.计算:
4.已知有理数m,n在数轴上的对应点的位置如图所示,则下列判断正确的是.
A.m>0
B.n<0
C.mn<0
D.m-n>0
C
5.填空:
-7的倒数是
,-0.6的倒数是
,
的倒数是
.
?
6.已知|a|=2,|b|=2,求ab的值.
6.
解:因为|a|=2,|b|=2,所以a=±2,b=±2.(1)当a=b=2时,ab=2×2=4;
(2)当a=2,b=-2时,ab=2×(-2)=-4;
(3)当a=-2,b=2时,ab=(-2)×2=-4;
(4)当a=-2,b=-2时,ab=(-2)×(-2)=4.
课堂总结
有理数的乘法
有理数的乘法法则
倒数
有理数的乘法的实际运用
2.任何数同0相乘,都得0.
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
有理数中,乘积是1的两个数互为倒数.
教材P30练习题1—3题.
课后作业
谢
谢
观
看
