青岛版八年级数学上册3.4分式的通分课件(共21张PPT)
文档属性
| 名称 | 青岛版八年级数学上册3.4分式的通分课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 717.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
3.4
分式的通分
学习目标:
1.理解分式通分的意义,掌握分式通分的方法及步骤;
2.通过与分数通分比较,渗透类比的思想方法。
1.分式的基本性质:
一个分式的分子与分母同乘(或除以)
一个
,分式的值___________
,
不变
(一)复习回顾
不为0的整式
2.什么叫约分?
利用分式的基本性质,把一个分式的分子和分母的公因式约去,
叫做分式的约分。
1.分数的通分:
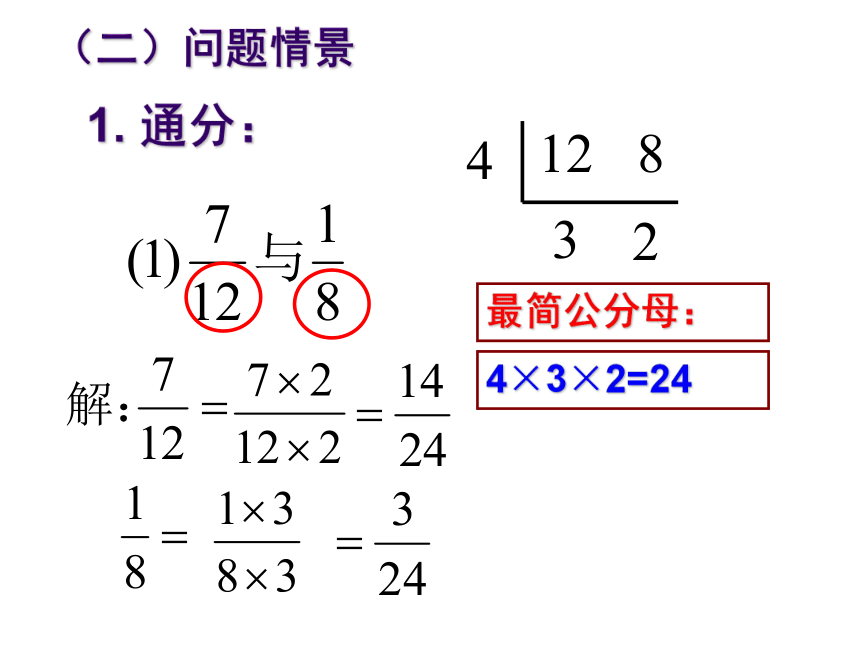
(二)问题情景
什么叫做分数的通分?
1.
通分:
最简公分母:
4×3×2=24
(二)问题情景
问题
类比分数的通分你能把下列分式化为分母相同的分式吗?
(二)问题情景
使分子和分母同乘适当的整式,不改变分式的值,把它们化成相同分母的分式,这样的分式变形叫做分式的通分.
如何进行分式通分?
试一试
你能把下列分式通分吗?
例题分析
通分:
最小
公倍数
最简
公分母
最高
次幂
单独字母
不同的因式
最简
公分母
例题分析
通分:
解:
最简公分母是
通分:
大显身手
解:
最简公分母是
1.怎样找最简公分母?
2.找最简公分母应从方面考虑?
第一要看系数;第二要看字母
通分要先确定分式的最简公分母。
方法归纳
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
确定最简公分母的一般步骤
(1)找系数:如果各分母的系数都是整数,那么取它们的最小公倍数。
(2)找字母:凡各分母因式中出现的所有字母或含字母的式子都要选取。
(3)找指数:取分母因式中出现的所有字母或含字母的式子中指数最大的。
(4)当分母是多项时,应先将各分母分解因式,再确定最简公分母
(5)分母的系数若是负数时,应利用符号法则,把负号提取到分式前面;
3.
三个分式
的最简公分母
是
1.三个分式
的最简公分母是(
)
B.
C.
D.
2.分式
的最简公分母是_________.
A.
课堂练习(补充)
(4)
(3)
(2)
(1)
课堂练习:通分
能力升级
知识梳理
1、把各分式化成相同分母的分式叫做
分式的通分.
2、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
课后作业
课本P63
习题3.4A组
第2题
3.
三个分式
的最简公分母
是
1.三个分式
的最简公分母是(
)
B.
C.
D.
2.分式
的最简公分母是_________.
A.
补充题目
最简公分母
3.4
分式的通分
学习目标:
1.理解分式通分的意义,掌握分式通分的方法及步骤;
2.通过与分数通分比较,渗透类比的思想方法。
1.分式的基本性质:
一个分式的分子与分母同乘(或除以)
一个
,分式的值___________
,
不变
(一)复习回顾
不为0的整式
2.什么叫约分?
利用分式的基本性质,把一个分式的分子和分母的公因式约去,
叫做分式的约分。
1.分数的通分:
(二)问题情景
什么叫做分数的通分?
1.
通分:
最简公分母:
4×3×2=24
(二)问题情景
问题
类比分数的通分你能把下列分式化为分母相同的分式吗?
(二)问题情景
使分子和分母同乘适当的整式,不改变分式的值,把它们化成相同分母的分式,这样的分式变形叫做分式的通分.
如何进行分式通分?
试一试
你能把下列分式通分吗?
例题分析
通分:
最小
公倍数
最简
公分母
最高
次幂
单独字母
不同的因式
最简
公分母
例题分析
通分:
解:
最简公分母是
通分:
大显身手
解:
最简公分母是
1.怎样找最简公分母?
2.找最简公分母应从方面考虑?
第一要看系数;第二要看字母
通分要先确定分式的最简公分母。
方法归纳
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
确定最简公分母的一般步骤
(1)找系数:如果各分母的系数都是整数,那么取它们的最小公倍数。
(2)找字母:凡各分母因式中出现的所有字母或含字母的式子都要选取。
(3)找指数:取分母因式中出现的所有字母或含字母的式子中指数最大的。
(4)当分母是多项时,应先将各分母分解因式,再确定最简公分母
(5)分母的系数若是负数时,应利用符号法则,把负号提取到分式前面;
3.
三个分式
的最简公分母
是
1.三个分式
的最简公分母是(
)
B.
C.
D.
2.分式
的最简公分母是_________.
A.
课堂练习(补充)
(4)
(3)
(2)
(1)
课堂练习:通分
能力升级
知识梳理
1、把各分式化成相同分母的分式叫做
分式的通分.
2、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
课后作业
课本P63
习题3.4A组
第2题
3.
三个分式
的最简公分母
是
1.三个分式
的最简公分母是(
)
B.
C.
D.
2.分式
的最简公分母是_________.
A.
补充题目
最简公分母
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
