青岛版八年级数学上册第一章 全等三角形复习(1)课件(共20张PPT)
文档属性
| 名称 | 青岛版八年级数学上册第一章 全等三角形复习(1)课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 14:20:06 | ||
图片预览


文档简介
(共20张PPT)
第一章全等三角形
复习课
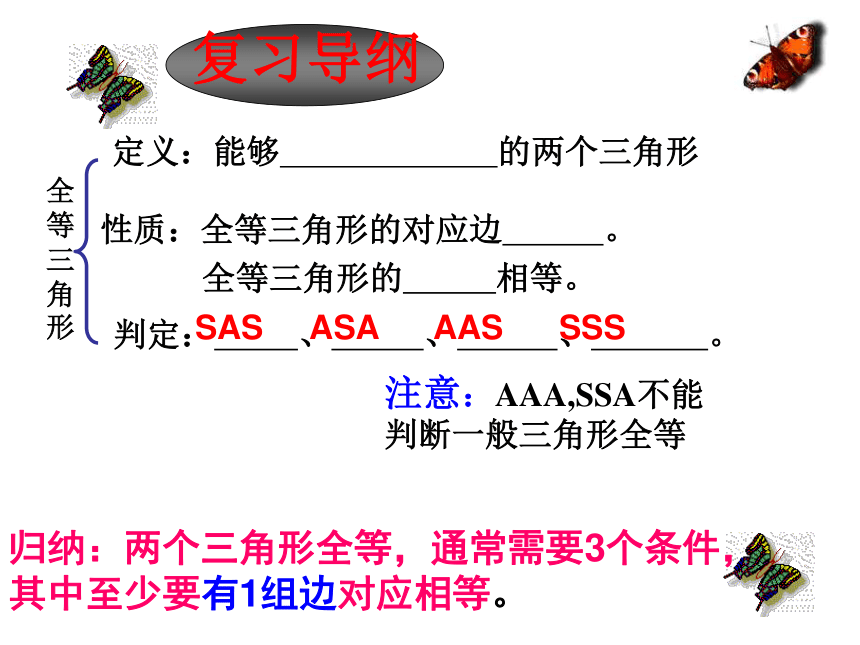
全等三角形
定义:能够
的两个三角形
性质:全等三角形的对应边
。
全等三角形的
相等。
判定:
、
、
、
。
归纳:两个三角形全等,通常需要3个条件,其中至少要有1组边对应相等。
SAS
ASA
AAS
SSS
注意:AAA,SSA不能判断一般三角形全等
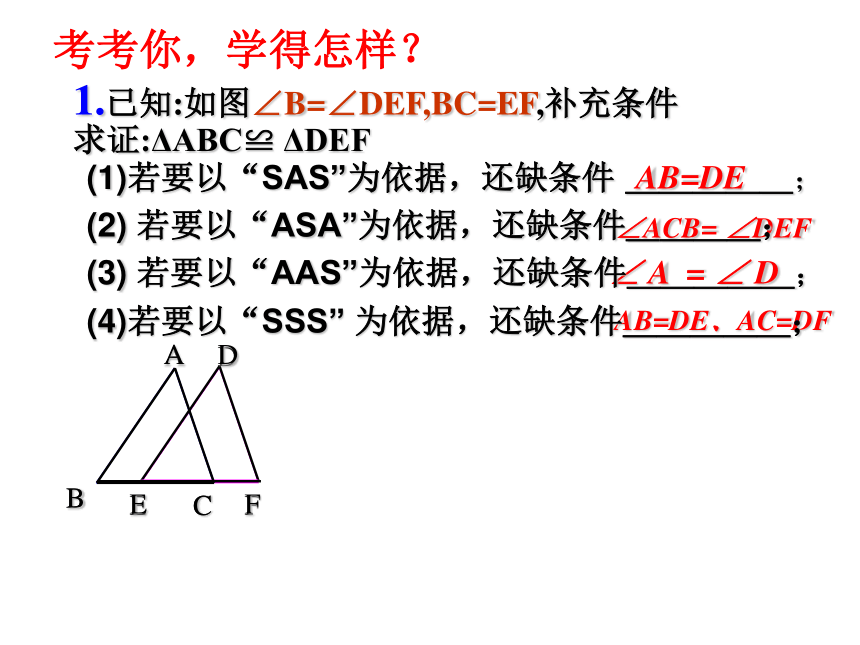
1.已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌
ΔDEF
∠ACB=
∠DEF
AB=DE
AB=DE、AC=DF
∠
A
=
∠
D
(1)若要以“SAS”为依据,还缺条件
_____;
(2)
若要以“ASA”为依据,还缺条件____;
(4)若要以“SSS”
为依据,还缺条件_____;
(3)
若要以“AAS”为依据,还缺条件_____;
考考你,学得怎样?
2、如图,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有( )
(A)1对
(B)2对 (C)3对 (D)4对
3、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等(B)两条直角边对应相等
(C)斜边和一直角边对应相等(D)两个锐角对应相等
4、下列四组中一定是全等三角形的为
(
)
A.三内角分别对应相等的两三角形
B、斜边相等的两直角三角形
C、两边和其中一条边的对角对应相等的两个三角形
D、三边对应相等的两个三角形
c
C
c
D
D
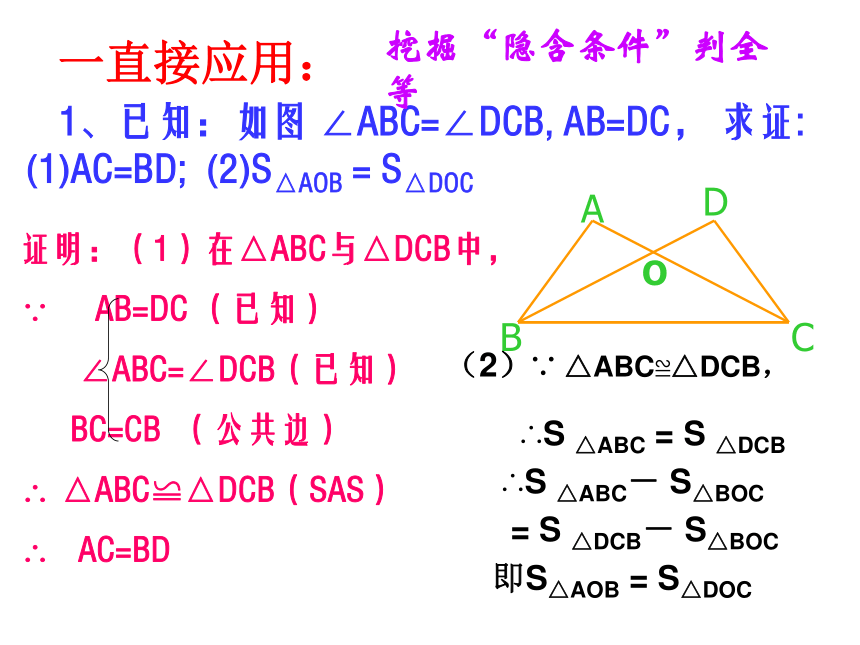
1、已知:如图
∠ABC=∠DCB,
AB=DC,
求证:
(1)AC=BD;
(2)S△AOB
=
S△DOC
(2)∵
△ABC≌△DCB,
∴S
△ABC
=
S
△DCB
∴S
△ABC-
S△BOC
=
S
△DCB-
S△BOC
即S△AOB
=
S△DOC
一直接应用:
挖掘“隐含条件”判全等
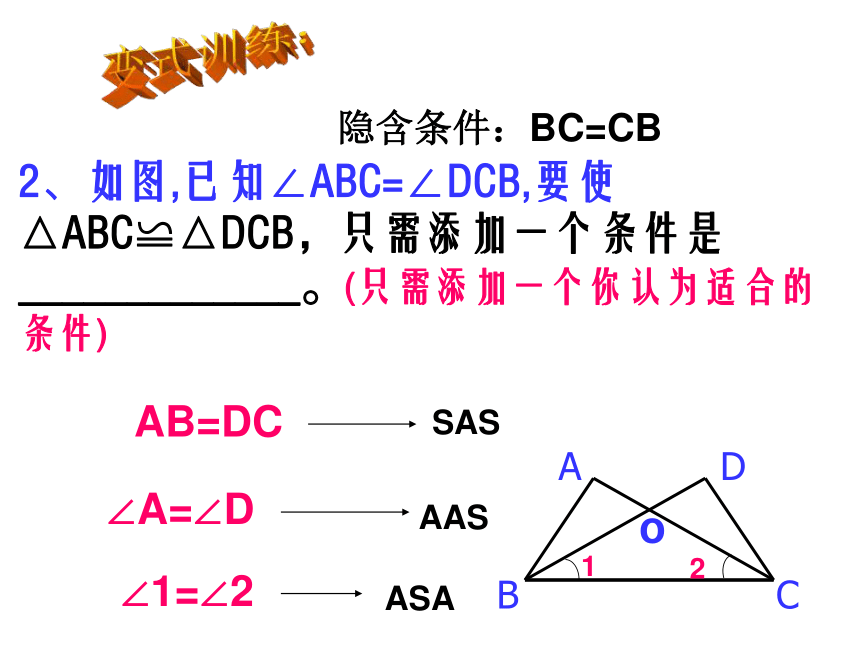
变式训练:
2、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是
_____________。(只需添加一个你认为适合的条件)
AB=DC
∠A=∠D
∠1=∠2
1
2
隐含条件:BC=CB
SAS
AAS
ASA
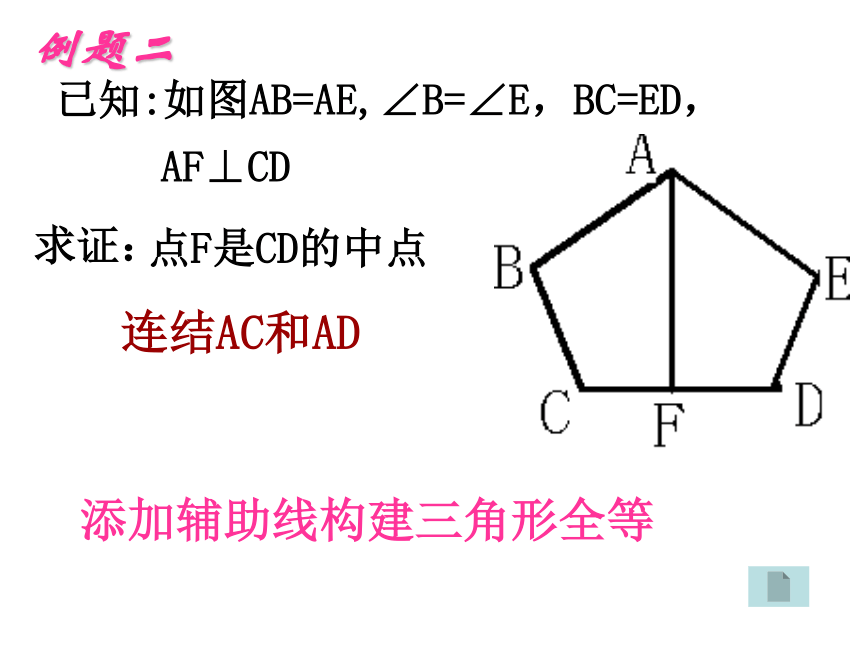
已知:如图AB=AE,∠B=∠E,BC=ED,
求证:
AF⊥CD
点F是CD的中点
连结AC和AD
例题二
添加辅助线构建三角形全等
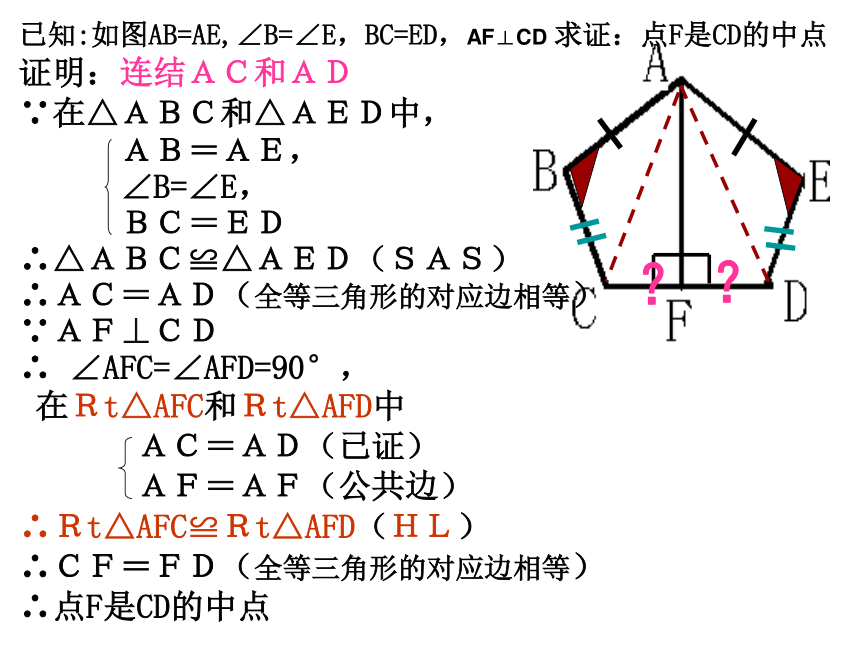
已知:如图AB=AE,∠B=∠E,BC=ED,AF⊥CD
求证:点F是CD的中点
证明:连结AC和AD
∵在△ABC和△AED中,
AB=AE,
∠B=∠E,
BC=ED
∴△ABC≌△AED(SAS)
∴AC=AD(全等三角形的对应边相等)
∵AF⊥CD
∴
∠AFC=∠AFD=90°,
在Rt△AFC和Rt△AFD中
AC=AD(已证)
AF=AF(公共边)
∴Rt△AFC≌Rt△AFD(HL)
∴CF=FD(全等三角形的对应边相等)
∴点F是CD的中点
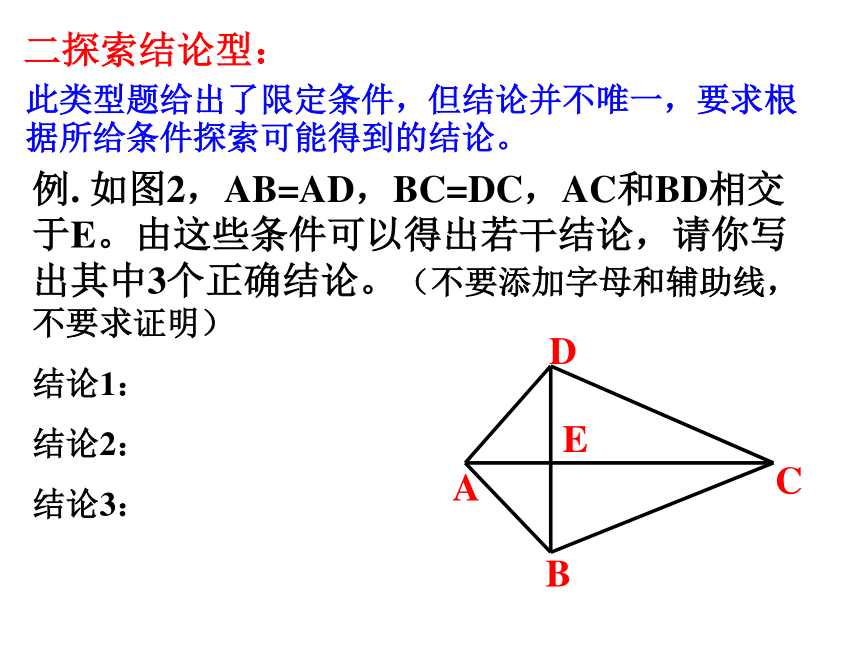
二探索结论型:
此类型题给出了限定条件,但结论并不唯一,要求根据所给条件探索可能得到的结论。
例.
如图2,AB=AD,BC=DC,AC和BD相交于E。由这些条件可以得出若干结论,请你写出其中3个正确结论。(不要添加字母和辅助线,不要求证明)
结论1:
结论2:
结论3:
三、探索方案型
此类型题首先提供一个实际问题背景,按照问题的要求研究解决问题的合理方案。
已知:A、B两点一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。
E
C
D
C
D
C
D
四、探索编拟问题型
例.
如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB,②AE=CF,③∠B=∠D,④
∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
1.如图1,CD与BE相交于点O,AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C=
,BE=
.
2.如图2,若OB=OD,∠A=∠C,若AB=3cm,则CD=
—
20°
5cm
3cm
友情提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!
反馈训练:
3.如图3,已知AC=BD,
∠A=∠D
,请你添一个直接条件,
=
,使△AFC≌△DEB
4、如图1,已知AC=BD,∠1=∠2,那么△ABC≌
, 其判定根据是__________。
5、
如图2,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___
=_____
___,
6、
如右图,已知AC=BD,
∠A=∠D
,请你添一个直接条件,
=
,△AFC≌△DEB
9.已知:如图,P是BD上的任意一点,AB=CB,AD=CD.
求证:
PA=PC
8.已知:如图∠B=∠D
,∠1=∠2,AB
=
AD
求证:ΔABC≌ΔADE
3
证明线段或角相等有时需通过两次全等来实现
10.
如图,AD⊥BC于D,AD=BD,AC=BE.
(1)
请说明∠1=∠C
(2)
猜想并说明DE和DC有何特殊关系?
O
D
P
C
A
B
11.已知:尺规作图作
的平分线方法如下:
以O为圆心,任意长为半径画弧交OA、OB于C、D
,
再分别以点C、D
为圆心,以大于
长为半径画弧,
,作射线
由作法得
的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
两弧交于点P
12.如图,在△ABE中,AB=AE,AD=AC,
∠BAD=∠EAC,
BC、DE交于点O.
求证:(1)
△ABC≌△AED;
(2)
OB=OE
.
.如图,AB=AC,CF⊥AB于F,BE⊥AC于E,
CF与BE交于H.
求证:(1)AH平分∠ABC;(2)CH=BH;
(3)连结BC与AH的延长线交于D,图中有多少对
全等三角形?为什么?
(4)交换“AB=AC”与“AH平分∠BAC”,
以上命题是否成立?为什么?
课后提升
祝
你
们
学
习
进
步
!
同学们
再见
第一章全等三角形
复习课
全等三角形
定义:能够
的两个三角形
性质:全等三角形的对应边
。
全等三角形的
相等。
判定:
、
、
、
。
归纳:两个三角形全等,通常需要3个条件,其中至少要有1组边对应相等。
SAS
ASA
AAS
SSS
注意:AAA,SSA不能判断一般三角形全等
1.已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌
ΔDEF
∠ACB=
∠DEF
AB=DE
AB=DE、AC=DF
∠
A
=
∠
D
(1)若要以“SAS”为依据,还缺条件
_____;
(2)
若要以“ASA”为依据,还缺条件____;
(4)若要以“SSS”
为依据,还缺条件_____;
(3)
若要以“AAS”为依据,还缺条件_____;
考考你,学得怎样?
2、如图,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有( )
(A)1对
(B)2对 (C)3对 (D)4对
3、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等(B)两条直角边对应相等
(C)斜边和一直角边对应相等(D)两个锐角对应相等
4、下列四组中一定是全等三角形的为
(
)
A.三内角分别对应相等的两三角形
B、斜边相等的两直角三角形
C、两边和其中一条边的对角对应相等的两个三角形
D、三边对应相等的两个三角形
c
C
c
D
D
1、已知:如图
∠ABC=∠DCB,
AB=DC,
求证:
(1)AC=BD;
(2)S△AOB
=
S△DOC
(2)∵
△ABC≌△DCB,
∴S
△ABC
=
S
△DCB
∴S
△ABC-
S△BOC
=
S
△DCB-
S△BOC
即S△AOB
=
S△DOC
一直接应用:
挖掘“隐含条件”判全等
变式训练:
2、如图,已知∠ABC=∠DCB,要使△ABC≌△DCB,只需添加一个条件是
_____________。(只需添加一个你认为适合的条件)
AB=DC
∠A=∠D
∠1=∠2
1
2
隐含条件:BC=CB
SAS
AAS
ASA
已知:如图AB=AE,∠B=∠E,BC=ED,
求证:
AF⊥CD
点F是CD的中点
连结AC和AD
例题二
添加辅助线构建三角形全等
已知:如图AB=AE,∠B=∠E,BC=ED,AF⊥CD
求证:点F是CD的中点
证明:连结AC和AD
∵在△ABC和△AED中,
AB=AE,
∠B=∠E,
BC=ED
∴△ABC≌△AED(SAS)
∴AC=AD(全等三角形的对应边相等)
∵AF⊥CD
∴
∠AFC=∠AFD=90°,
在Rt△AFC和Rt△AFD中
AC=AD(已证)
AF=AF(公共边)
∴Rt△AFC≌Rt△AFD(HL)
∴CF=FD(全等三角形的对应边相等)
∴点F是CD的中点
二探索结论型:
此类型题给出了限定条件,但结论并不唯一,要求根据所给条件探索可能得到的结论。
例.
如图2,AB=AD,BC=DC,AC和BD相交于E。由这些条件可以得出若干结论,请你写出其中3个正确结论。(不要添加字母和辅助线,不要求证明)
结论1:
结论2:
结论3:
三、探索方案型
此类型题首先提供一个实际问题背景,按照问题的要求研究解决问题的合理方案。
已知:A、B两点一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。
E
C
D
C
D
C
D
四、探索编拟问题型
例.
如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB,②AE=CF,③∠B=∠D,④
∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
1.如图1,CD与BE相交于点O,AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C=
,BE=
.
2.如图2,若OB=OD,∠A=∠C,若AB=3cm,则CD=
—
20°
5cm
3cm
友情提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!
反馈训练:
3.如图3,已知AC=BD,
∠A=∠D
,请你添一个直接条件,
=
,使△AFC≌△DEB
4、如图1,已知AC=BD,∠1=∠2,那么△ABC≌
, 其判定根据是__________。
5、
如图2,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___
=_____
___,
6、
如右图,已知AC=BD,
∠A=∠D
,请你添一个直接条件,
=
,△AFC≌△DEB
9.已知:如图,P是BD上的任意一点,AB=CB,AD=CD.
求证:
PA=PC
8.已知:如图∠B=∠D
,∠1=∠2,AB
=
AD
求证:ΔABC≌ΔADE
3
证明线段或角相等有时需通过两次全等来实现
10.
如图,AD⊥BC于D,AD=BD,AC=BE.
(1)
请说明∠1=∠C
(2)
猜想并说明DE和DC有何特殊关系?
O
D
P
C
A
B
11.已知:尺规作图作
的平分线方法如下:
以O为圆心,任意长为半径画弧交OA、OB于C、D
,
再分别以点C、D
为圆心,以大于
长为半径画弧,
,作射线
由作法得
的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
两弧交于点P
12.如图,在△ABE中,AB=AE,AD=AC,
∠BAD=∠EAC,
BC、DE交于点O.
求证:(1)
△ABC≌△AED;
(2)
OB=OE
.
.如图,AB=AC,CF⊥AB于F,BE⊥AC于E,
CF与BE交于H.
求证:(1)AH平分∠ABC;(2)CH=BH;
(3)连结BC与AH的延长线交于D,图中有多少对
全等三角形?为什么?
(4)交换“AB=AC”与“AH平分∠BAC”,
以上命题是否成立?为什么?
课后提升
祝
你
们
学
习
进
步
!
同学们
再见
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
