10.4 平行线的判定第1课时

七年级数学导学案 第十章 平行线
10．4平行线和它的画法（第1课时）
执笔人：实验中学 审稿人：实验中学
一、学习目标： 1. 经历平行线判定方法的导出过程。
2. 会依据具体条件判定两直线平行。
二、学习重点和难点
重点：探索平行线判定的条件。
难点：熟练掌握两直线平行的判定．
三、学法指导：观察感悟，类比推理。
四、学习过程：
学生上课前自主完成部分
【课前预习及预习感悟】依据预习提纲完成下列问题
◆自学教科书P34至P36“实验与探究”和“交流与发现”部分，并完成下列问题：
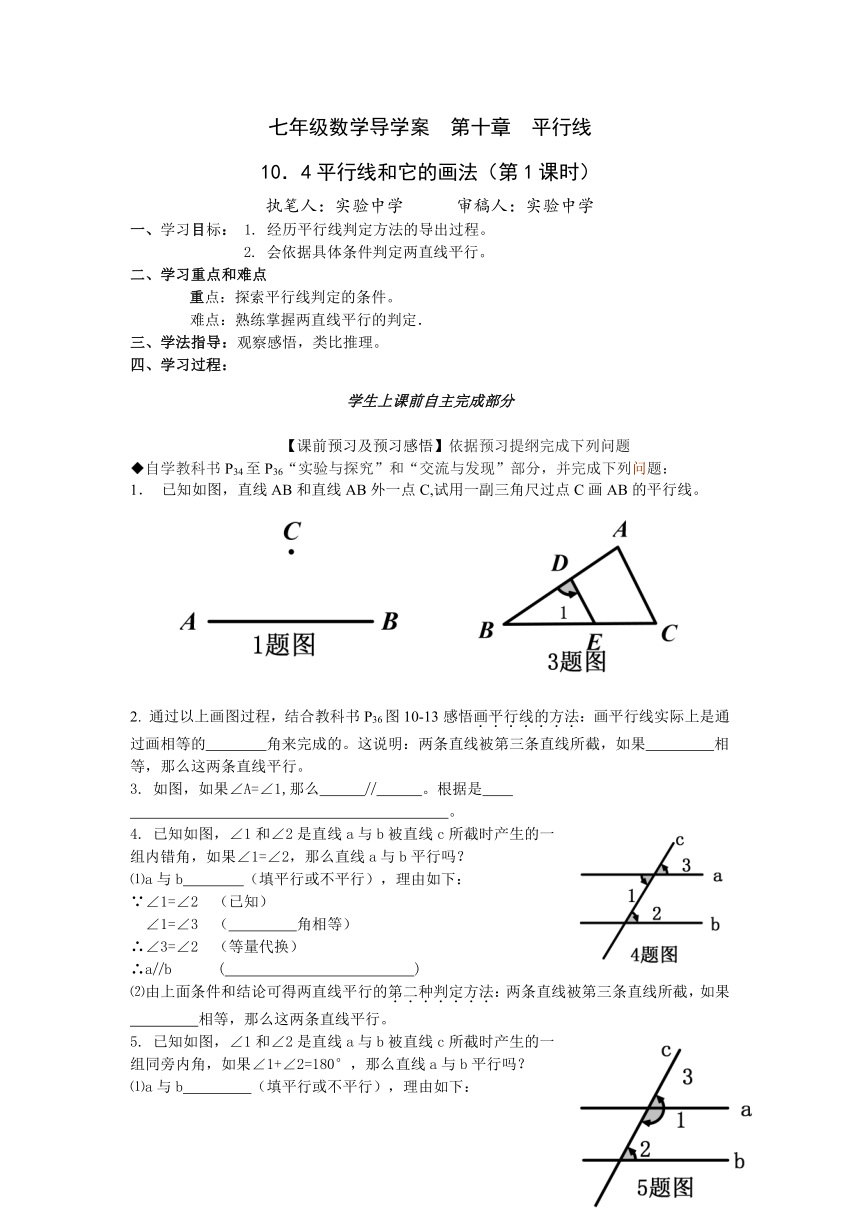
已知如图，直线AB和直线AB外一点C,试用一副三角尺过点C画AB的平行线。
2. 通过以上画图过程，结合教科书P36图10-13感悟画平行线的方法：画平行线实际上是通过画相等的 角来完成的。这说明：两条直线被第三条直线所截，如果 相等，那么这两条直线平行。
3. 如图，如果∠A=∠1,那么 // 。根据是
。
4. 已知如图，∠1和∠2是直线a与b被直线c所截时产生的一组内错角，如果∠1=∠2，那么直线a与b平行吗？
⑴a与b （填平行或不平行），理由如下：
∵∠1=∠2 （已知）
∠1=∠3 （ 角相等）
∴∠3=∠2 （等量代换）
∴a//b ( )
⑵由上面条件和结论可得两直线平行的第二种判定方法：两条直线被第三条直线所截，如果
相等，那么这两条直线平行。
5. 已知如图，∠1和∠2是直线a与b被直线c所截时产生的一组同旁内角，如果∠1+∠2=180°，那么直线a与b平行吗？
⑴a与b （填平行或不平行），理由如下：
∵∠1+∠2=180° （ ）
∠1+∠3=180° （邻补角的定义）
∴∠3=∠2 （同角的 相等）
∴a//b （ ）
⑵由上面条件和结论可得两直线平行的第三种判定方法：两条直线被第三条直线所截，如果同旁内角 ，那么这两条直线平行。
6. 如图已知，a//c，b//c，那么直线a与b平行吗？
⑴a与b （填平行或不平行），理由如下：
∵a//c （ ）
∴∠1=∠2 （ ）
∵b//c （ ）
∴∠3=∠2 （ ）
∴∠1=∠3 （ ）
∴a//b （ ）
⑵由上面条件和结论可得两直线平行的第四种判定方法：如果两条直线都和第三条直线 ，那么这两条直线也平行
◆预习疑难摘要：
师生课上共同完成部分
【课堂学习研讨交流】
1小组交流预习中有关平行线判定中的疑难问题，不会的与同学和老师交流
2 总结平行线的判定方法，与同学交流。
【知识应用与能力形成】
如图所示，请推理填空。
⑴∵∠A=＿＿＿ （已知）
∴AC//DE（ ）
⑵∵∠2=＿＿＿ （已知）
∴AC//DE（ ）
⑶∵∠A+＿＿＿=180°（已知）
∴AB//FD（ ）
⑷∵∠2+＿＿＿=180°（已知）
∴AC//DE（ ）
⑸∵∠3= （已知）
∴AB//FD（ ）
例题分析：本题从结论入手去追溯能使结论成立的原因，即执果索因，无论添加任何条件，目的是满足同位角相等或内错角相等或同旁内角互补，从而得出平行。
如图所示，由下列条件可判定哪两条直线平行
⑴∠1=∠3
⑵∠2=∠4
例题分析：要分析清楚∠1和∠3，∠2和∠4分别是哪两条直线被哪条直线所截产生的内错角。
◆课内巩固训练
如图，已知∠1=116°，∠2=116°，直线a与直线b平行吗？为什么？
如图，已知∠1=50°，当∠2= 时，a//b，为什么？
【学习体会】　
1. 本节课你有何收获和困惑？在课本和学案上划出来并与同学和老师交流。
2. 关于平行线的判定你掌握了哪些方法，先自己总结一下，再与同学和老师交流。
【基础达标】
1. 如图，有由下列条件可以判定哪两条直线平行？说明理由。
⑴ ∠1=∠2
⑵ ∠4=∠A
⑶ ∠A+∠2+∠3=180°
2. 如图，由∠A与∠B互补可以判定 // ，根据是
3. 如图，D为AC上的一点，E是AB上的一点。
在什么条件下能够判定DE//BC 说明理由。
4. 已知如图，AD与BC交于点O, ∠A=∠D, ∠B=40°,则∠C=
五 综合与提升（必做作业；做在作业本上）
1.（ 教科书P38 A组 3 ) 2.（教科书P39 A组 4）
课下完成部分；时间充足可课上完成
六 拓展与探究（选做作业）
１.如图所示，AB//CD,GH平分∠DGE,IJ平分∠BIE.猜测GH与IJ的关系，并予以说明理由。