1.5.1有理数乘法运算律(2)-湘教版七年级数学上册课件(共24张PPT)
文档属性
| 名称 | 1.5.1有理数乘法运算律(2)-湘教版七年级数学上册课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第1章
有理数
第2课时
有理数乘法运算律
湘教版
七年级上册
学习目标
1.掌握乘法的分配律,并能灵活的运用.(难点)
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.(重点)
1.有理数乘法法则是什么?
2.如何进行有理数的乘法运算?
3.小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数和零相乘,都得0.
1.先确定积的符号.
2.计算积的绝对值.
乘法交换律、乘法结合律、乘法分配律
复习巩固
问题引入
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
引入负数后,三种运算律是否还成立呢?
填空:
(1)(-2)×4=
,
4×(-2)=
;
-8
-8
动脑筋
(2)[(-2)×(-3)]
×(-4)=
×(-4)=
,
(-2)×[(-3)
×(-4)]=(-2)×
=
.
6
-24
12
-24
从上面的填空题中,你发现了什么?
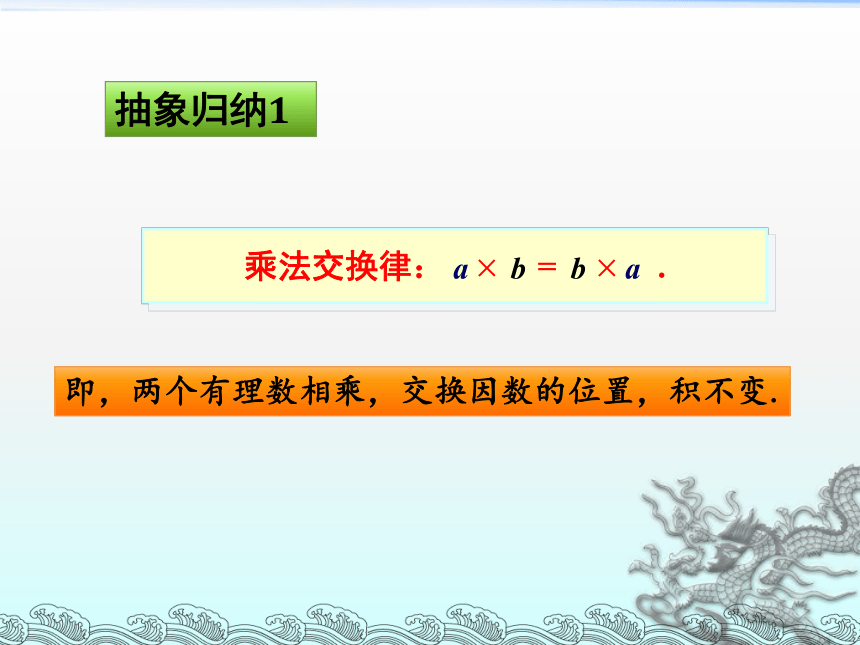
抽象归纳1
乘法交换律:
×
=
×
.
a
b
a
b
即,两个有理数相乘,交换因数的位置,积不变.
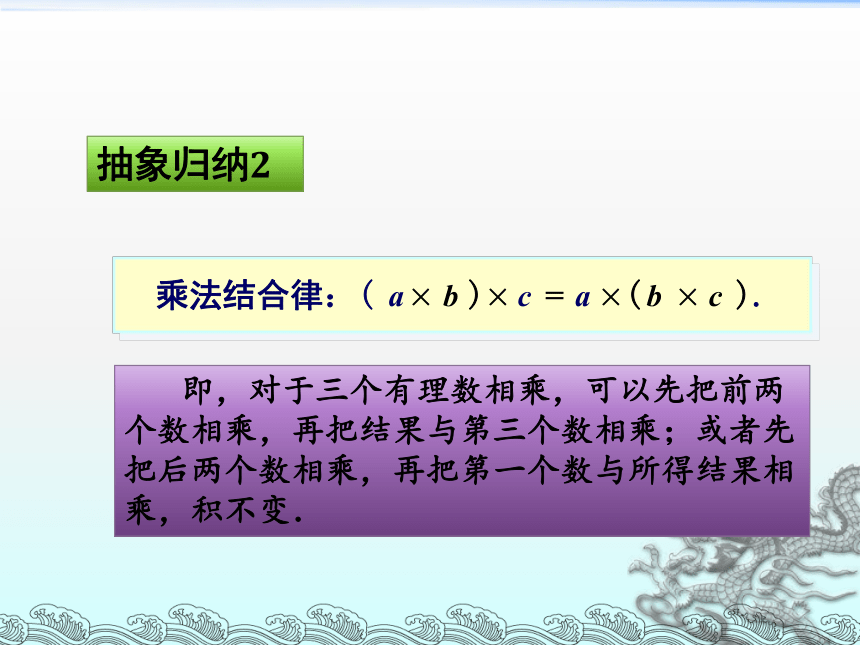
乘法结合律:(
×
)×
=
×(
×
).
a
b
a
b
c
c
即,对于三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变.
抽象归纳2
和加法类似,根据乘法交换律和乘法结合律可以推出:三个或三个以上有理数相乘,可以写成这些数的连乘式.对于连乘式,可以任意交换因数的位置,也可先把其中的几个数相乘.
(1)填空:
动脑筋
(-6)×[4+(-9)]
=(-6)×
=
,
(-6)×4+(-6)×(-9)=
+
=
.
-5
30
54
-24
30
(2)换几个有理数试一试,你发现了什么?
乘法对加法的分配律(简称为分配律):
×(
+
)
=
×
+
×
.
b
c
a
a
b
a
c
(-1)a
=
-a
利用分配律,可以得出
即,一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
抽象归纳3
例1
计算:
例题解析
例2
计算:
解:
(3)(-0.1)×(-100)×0.01×(-10).
解:(-0.1)×(-100)×0.01×(-10)
=-(0.1×100×0.01×10)
=-[(0.1×10)×(100×0.01)]
=-1
乘法交换律、结合律
①
(-8)×(-12)×(-0.125)×(-
)×(-0.1)
1
3
②
60×(1-
-
-
)
1
2
1
3
1
4
③
(-
)×(8-1
-4
)
3
4
1
3
④
(-11)×(-
)+(-11)×2
+(-11)×(-
)
2
5
3
5
1
5
计算:
答案
①
-0.4
②-5
③-2
④-22
练一练
问题
观察下列各式,它们的积是正还是负?
(1)(-1)×2×3×4
(2)(-1)×(-2)×3×4
(3)(-1)×(-2)×(-3)×4
(4)(-1)×(-2)×(-3)×(-4)
(5)(-1)×(-2)×(-3)×(-4)×0
多个有理数相乘
负
正
负
正
零
思考
多个有理数相乘,有一个因数为0,积是多少?因数都不为0时,积的符号和负因数的个数有什么关系?
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定:?当负因数的个数为奇数时,积为负;
?当负因数的个数为偶数时,积为正.
总结归纳
1.判断下列各式的积是正还是负?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
练一练
例3
计算:
解:(1)原式
(2)原式
先确定积的符号
再确定积的绝对值
例3
计算:
课堂练习
1.计算(-2)×(3-
),用乘法分配律计算过程正确的是
(
)
A.(-2)×3+(-2)×(-
)
B.(-2)×3-(-2)×(-
)
C.2×3-(-2)×(-
)
D.(-2)×3+2×(-
)
A
2.三个数的乘积为0,则(
)
A.三个数一定都为0
B.一个数为0,其他两个不为0
C.至少有一个是0
D.两个数为0,另一个不为0
C
4.计算:
解:
4.计算:
1.乘法交换律:a×b=b×a,即两个有理数相乘,交换因数的位置,积不变.
课堂小结:
2.乘法结合律:(a×b)×c=a×(b×c),即三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变.
3.乘法对加法的分配律:a×(b+c)=a×b+a×c,即一个有理数和两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
4.几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正
.
第1章
有理数
第2课时
有理数乘法运算律
湘教版
七年级上册
学习目标
1.掌握乘法的分配律,并能灵活的运用.(难点)
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.(重点)
1.有理数乘法法则是什么?
2.如何进行有理数的乘法运算?
3.小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数和零相乘,都得0.
1.先确定积的符号.
2.计算积的绝对值.
乘法交换律、乘法结合律、乘法分配律
复习巩固
问题引入
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
引入负数后,三种运算律是否还成立呢?
填空:
(1)(-2)×4=
,
4×(-2)=
;
-8
-8
动脑筋
(2)[(-2)×(-3)]
×(-4)=
×(-4)=
,
(-2)×[(-3)
×(-4)]=(-2)×
=
.
6
-24
12
-24
从上面的填空题中,你发现了什么?
抽象归纳1
乘法交换律:
×
=
×
.
a
b
a
b
即,两个有理数相乘,交换因数的位置,积不变.
乘法结合律:(
×
)×
=
×(
×
).
a
b
a
b
c
c
即,对于三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变.
抽象归纳2
和加法类似,根据乘法交换律和乘法结合律可以推出:三个或三个以上有理数相乘,可以写成这些数的连乘式.对于连乘式,可以任意交换因数的位置,也可先把其中的几个数相乘.
(1)填空:
动脑筋
(-6)×[4+(-9)]
=(-6)×
=
,
(-6)×4+(-6)×(-9)=
+
=
.
-5
30
54
-24
30
(2)换几个有理数试一试,你发现了什么?
乘法对加法的分配律(简称为分配律):
×(
+
)
=
×
+
×
.
b
c
a
a
b
a
c
(-1)a
=
-a
利用分配律,可以得出
即,一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
抽象归纳3
例1
计算:
例题解析
例2
计算:
解:
(3)(-0.1)×(-100)×0.01×(-10).
解:(-0.1)×(-100)×0.01×(-10)
=-(0.1×100×0.01×10)
=-[(0.1×10)×(100×0.01)]
=-1
乘法交换律、结合律
①
(-8)×(-12)×(-0.125)×(-
)×(-0.1)
1
3
②
60×(1-
-
-
)
1
2
1
3
1
4
③
(-
)×(8-1
-4
)
3
4
1
3
④
(-11)×(-
)+(-11)×2
+(-11)×(-
)
2
5
3
5
1
5
计算:
答案
①
-0.4
②-5
③-2
④-22
练一练
问题
观察下列各式,它们的积是正还是负?
(1)(-1)×2×3×4
(2)(-1)×(-2)×3×4
(3)(-1)×(-2)×(-3)×4
(4)(-1)×(-2)×(-3)×(-4)
(5)(-1)×(-2)×(-3)×(-4)×0
多个有理数相乘
负
正
负
正
零
思考
多个有理数相乘,有一个因数为0,积是多少?因数都不为0时,积的符号和负因数的个数有什么关系?
几个数相乘,有一个因数为0,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定:?当负因数的个数为奇数时,积为负;
?当负因数的个数为偶数时,积为正.
总结归纳
1.判断下列各式的积是正还是负?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
练一练
例3
计算:
解:(1)原式
(2)原式
先确定积的符号
再确定积的绝对值
例3
计算:
课堂练习
1.计算(-2)×(3-
),用乘法分配律计算过程正确的是
(
)
A.(-2)×3+(-2)×(-
)
B.(-2)×3-(-2)×(-
)
C.2×3-(-2)×(-
)
D.(-2)×3+2×(-
)
A
2.三个数的乘积为0,则(
)
A.三个数一定都为0
B.一个数为0,其他两个不为0
C.至少有一个是0
D.两个数为0,另一个不为0
C
4.计算:
解:
4.计算:
1.乘法交换律:a×b=b×a,即两个有理数相乘,交换因数的位置,积不变.
课堂小结:
2.乘法结合律:(a×b)×c=a×(b×c),即三个有理数相乘,可以先把前两个数相乘,再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变.
3.乘法对加法的分配律:a×(b+c)=a×b+a×c,即一个有理数和两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
4.几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正
.
同课章节目录
