人教版八年级上册数学课件:11.1.1三角形的边 (共29张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:11.1.1三角形的边 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 12:20:15 | ||
图片预览





文档简介
(共29张PPT)
11.1.1
三角形的边
生活中的三角形!
生活中的三角形!
旧知回顾
我们小学时是怎样给三角形定义的?
是否任意长度的三条线段都能首尾顺次连结?
三角形的定义
A
B
C
a
b
c
不在同一条直线上的
三条线段首尾顺次相接组成的图形。
三角形的特征有:
(1)三条线段
(2)不在同一直线上
(3)首尾顺次连接
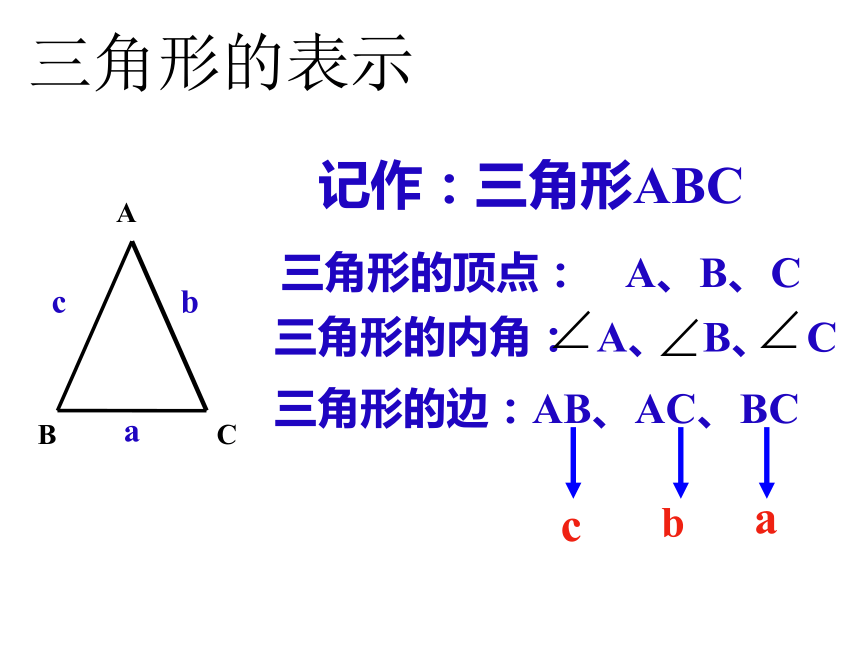
三角形的表示
A
B
C
a
b
c
记作:三角形ABC
三角形的顶点:
A、B、C
三角形的边:AB、AC、BC
三角形的内角:
A、
B、
C
c
b
a
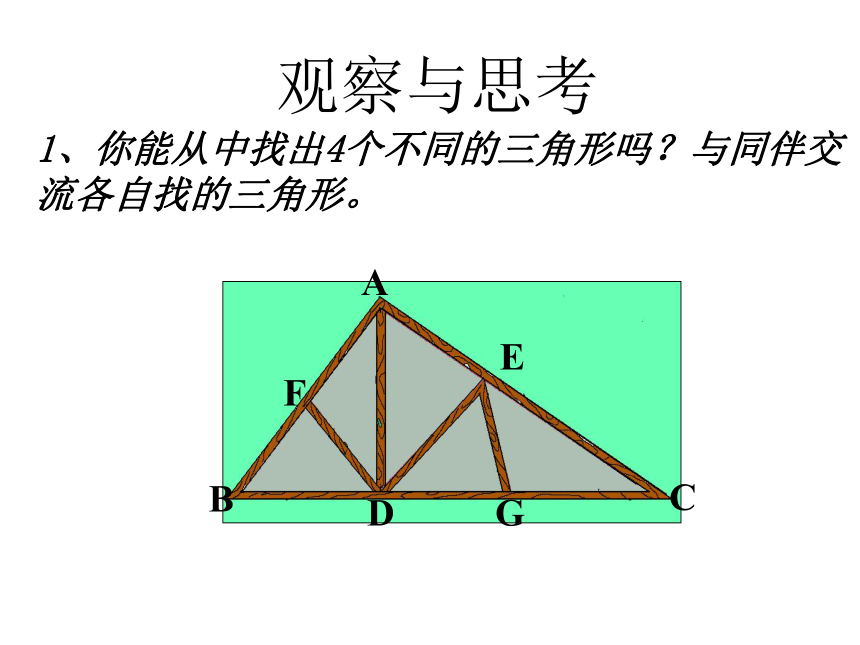
观察与思考
1、你能从中找出4个不同的三角形吗?与同伴交流各自找的三角形。
E
D
E
F
G
A
B
C
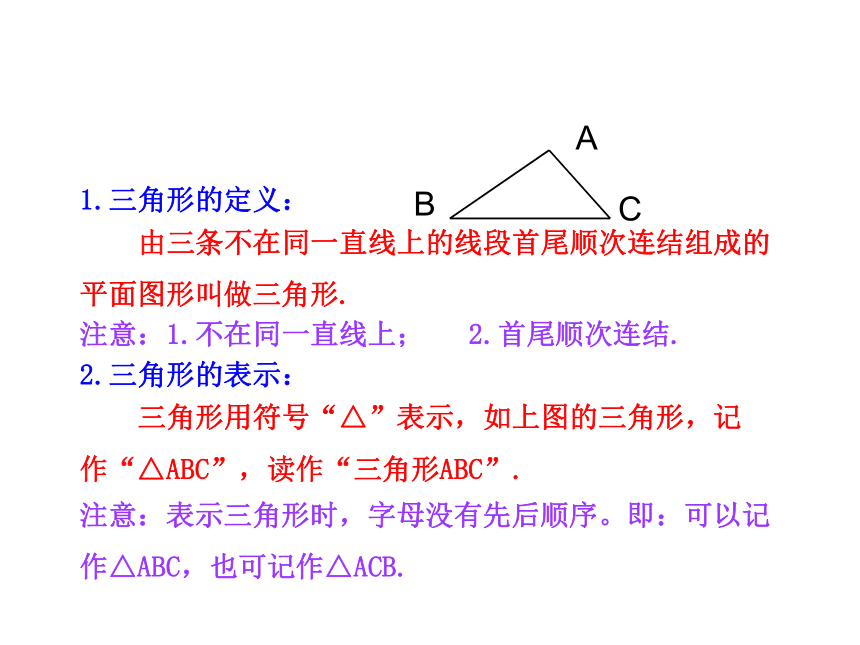
由三条不在同一直线上的线段首尾顺次连结组成的平面图形叫做三角形.
注意:1.不在同一直线上;
2.首尾顺次连结.
注意:表示三角形时,字母没有先后顺序。即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
如图,△ABC的三个顶点分别是:A、B、C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB、BC、CA。
它的三个角分别是:
?A=
?
BAC、
?B=
?
ABC、
?C=
?ABC.
A
B
C
a
b
c
4.三角形的边、内角
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
只有两条边相等的三角形
等边三角形
思考:
任意长度的3条线段都可以围成三角形吗?
两边的和小于第三边,
不能围成三角形。
5
6
12
两边的和等于第三边,
不能围成三角形。
5
7
12
大胆猜测:
两根小棒的长度之和与第三根小棒存在什么关系时,就能围成三角形呢?
两边的和小于第三边,不能围成三角形。
两边的和等于第三边,不能围成三角形。
两边的和大于第三边,能围成三角形。
猜想:
任意两边之和大于第三边,
能围成三角形。
5
6
7
下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
5,6,10
(
)
(4)
3,5,8
(
)
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
1、下列各组线段能围成三角形吗?
1、4cm
,9cm,
5cm
(
)
2、8cm
,1cm,
6cm
(
)
3、3cm
,3cm,
3cm
(
)
2、若三角形的两边长分别是4和10,第三边长可能是(
).
A.5
B.6
C.11
D.16
3、若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
答:第三边的长为7。
4、下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)3cm,
4cm,
5cm
(2)8cm,
7cm,
15cm
(3)
13cm,
12cm,
20cm
(4)5cm,
5cm,
11cm
(1)(3)
5、如果三角形的两边长分别是2和4,且第三边是奇数,
那么第三边长为
.若第三边为偶数,那么三角形的周长
.
3或5
10
6、有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7
<
8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
7.在如图所示的图形中,三角形的个数共有(
)
A.1个
B.2个
C.
3个
D.4个
选C.
图中有△ABC,△ABD,△ACD.
8、小强用三根木棒组成的图形,其中符合三角形概念是
(
)
B
A
C
C
9、找一找,图中有多少个三角形,并把它们写下来.
图中有5个三角形.分别是:
△ABE、
△DEC、
△BEC、
△ABC、
△DBC
10、下列长度的三条线段,不能组
成三角形的是(
)
A.3,8,4
B.4,9,6
C.15,20,8
D.9,15,8
选A.因为3+4=7<8,出现两边之和小于第三边的情况,所以不能组成三角形.
11、若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是(
)
A.1
B.5
C.7
D.9
选B.设第三边为x,则1<x<7.
12、已知一个三角形的三边a=7,b=3,第三边c是一个正整数,满足这些条件的三角形共有
种,当c=
时,所作出的三角形的周长最长.
根据三角形的形成条件:两边之和大于第三边,两边之差小于第三边.
可知第三边的取值范围为4<c<10,因为c是正整数,所以c=5,6,7,8,9.
答案:5
9
概念
三角形
分类
表示方法
三边关系
通过本课时的学习,需要我们掌握
11.1.1
三角形的边
生活中的三角形!
生活中的三角形!
旧知回顾
我们小学时是怎样给三角形定义的?
是否任意长度的三条线段都能首尾顺次连结?
三角形的定义
A
B
C
a
b
c
不在同一条直线上的
三条线段首尾顺次相接组成的图形。
三角形的特征有:
(1)三条线段
(2)不在同一直线上
(3)首尾顺次连接
三角形的表示
A
B
C
a
b
c
记作:三角形ABC
三角形的顶点:
A、B、C
三角形的边:AB、AC、BC
三角形的内角:
A、
B、
C
c
b
a
观察与思考
1、你能从中找出4个不同的三角形吗?与同伴交流各自找的三角形。
E
D
E
F
G
A
B
C
由三条不在同一直线上的线段首尾顺次连结组成的平面图形叫做三角形.
注意:1.不在同一直线上;
2.首尾顺次连结.
注意:表示三角形时,字母没有先后顺序。即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
如图,△ABC的三个顶点分别是:A、B、C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB、BC、CA。
它的三个角分别是:
?A=
?
BAC、
?B=
?
ABC、
?C=
?ABC.
A
B
C
a
b
c
4.三角形的边、内角
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
只有两条边相等的三角形
等边三角形
思考:
任意长度的3条线段都可以围成三角形吗?
两边的和小于第三边,
不能围成三角形。
5
6
12
两边的和等于第三边,
不能围成三角形。
5
7
12
大胆猜测:
两根小棒的长度之和与第三根小棒存在什么关系时,就能围成三角形呢?
两边的和小于第三边,不能围成三角形。
两边的和等于第三边,不能围成三角形。
两边的和大于第三边,能围成三角形。
猜想:
任意两边之和大于第三边,
能围成三角形。
5
6
7
下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
5,6,10
(
)
(4)
3,5,8
(
)
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?有没有更简便的判断方法?
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
1、下列各组线段能围成三角形吗?
1、4cm
,9cm,
5cm
(
)
2、8cm
,1cm,
6cm
(
)
3、3cm
,3cm,
3cm
(
)
2、若三角形的两边长分别是4和10,第三边长可能是(
).
A.5
B.6
C.11
D.16
3、若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
答:第三边的长为7。
4、下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)3cm,
4cm,
5cm
(2)8cm,
7cm,
15cm
(3)
13cm,
12cm,
20cm
(4)5cm,
5cm,
11cm
(1)(3)
5、如果三角形的两边长分别是2和4,且第三边是奇数,
那么第三边长为
.若第三边为偶数,那么三角形的周长
.
3或5
10
6、有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7
<
8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
7.在如图所示的图形中,三角形的个数共有(
)
A.1个
B.2个
C.
3个
D.4个
选C.
图中有△ABC,△ABD,△ACD.
8、小强用三根木棒组成的图形,其中符合三角形概念是
(
)
B
A
C
C
9、找一找,图中有多少个三角形,并把它们写下来.
图中有5个三角形.分别是:
△ABE、
△DEC、
△BEC、
△ABC、
△DBC
10、下列长度的三条线段,不能组
成三角形的是(
)
A.3,8,4
B.4,9,6
C.15,20,8
D.9,15,8
选A.因为3+4=7<8,出现两边之和小于第三边的情况,所以不能组成三角形.
11、若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是(
)
A.1
B.5
C.7
D.9
选B.设第三边为x,则1<x<7.
12、已知一个三角形的三边a=7,b=3,第三边c是一个正整数,满足这些条件的三角形共有
种,当c=
时,所作出的三角形的周长最长.
根据三角形的形成条件:两边之和大于第三边,两边之差小于第三边.
可知第三边的取值范围为4<c<10,因为c是正整数,所以c=5,6,7,8,9.
答案:5
9
概念
三角形
分类
表示方法
三边关系
通过本课时的学习,需要我们掌握
