14.2.2 完全平方公式课件(共27张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 15:50:40 | ||
图片预览







文档简介
(共27张PPT)
人教版
八年级数学上
14.2.2完全平方公式
学习目标
1.理解并掌握完全平方公式的推导过程、结构特点、
几何解释.(重点)
2.灵活应用完全平方公式进行计算.(难点)
回顾旧知
2.填空:
1.说一说乘法的平方差公式?
两个数的和与这两个数的差的积,等于这两个数的平方差.
合作探究
思考1:
计算下列多项式的积,你能发现什么规律?
思考2:
根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2=
.
a2+2ab+b2
(a-b)2=
.
a2-2ab+b2
合作探究
完全平方公式:
(a+b)2=
.
a2+2ab+b2
(a-b)2=
.
a2-2ab+b2
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为:
“首平方,尾平方,积的2倍放中间”
合作探究
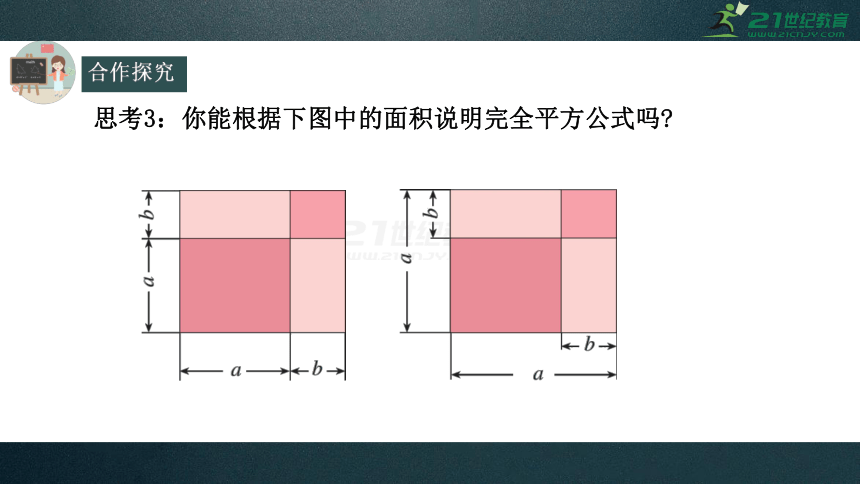
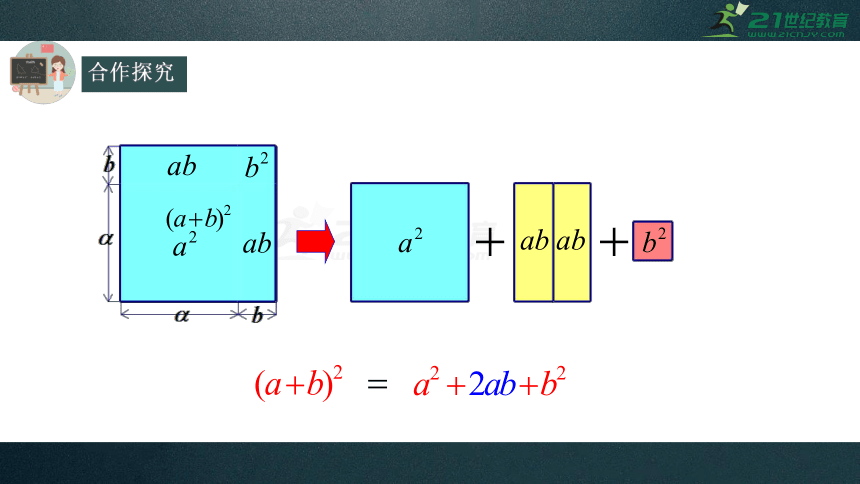
思考3:你能根据下图中的面积说明完全平方公式吗?
合作探究
合作探究
合作探究
(a+b)2=
a2+2ab+b2.
(a-b)2=a2-2ab+b2.
思考4:观察下面两个完全平方式,比一比,回答下列问题:
1.说一说积的次数和项数.
2.两个完全平方式的积有相同的项吗?与a,b有什么关系?
3.两个完全平方式的积中不同的是哪一项?与
a,b有什么关系?它的符号与什么有关?
合作探究
公式特征:
3.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和,另一项是两数积的2倍,且与两数中
间的符号相同
;
针对训练
1、下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(a+b)2=a2
+b2
(2)(a-b)2
=a2
–ab+b2
(3)
(-x
+y)2
=x2+2xy
+y2
(4)
(2x+y)2
=4x2
+2xy
+y2
×
×
×
×
(a
+b)2
=a2+2ab
+b2
(a
-b)2
=a2
-2ab
+b2
(-x
+y)2
=x2
-2xy
+y2
(2x
+y)2
=4x2+4xy
+y2
典例精析
例1.用完全平方公式计算:
解:
典例精析
(1)
1022;
解:
1022
=
(100+2)2
=10000+400+4
=10404.
(2)
992.
992
=
(100
–1)2
=10000
-200+1
=9801.
例2
运用完全平方公式计算:
知识点拨:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
小试牛刀
1、利用完全平方公式计算:
(1)(x+6)2;
(2)(-3m-4n)2;
(3)(-3a+b)2.
(3)(-3a+b)2=9a2-6ab+b2.
解:(1)(x+6)2=x2+12x+36;
(2)(-3m-4n)2=9m2+24mn+16n2;
那
(-x-6)2呢?
它与(b-3a)2的值相等吗?
知识点拨:
(a+b)2
与(-a-b)2
相等,
(a-b)2
与(b-a)2相等。
(a-b)2与a2-b2值相等吗?为什么?
小试牛刀
2、利用乘法公式计算:
(1)982-101×99;
(2)20202-2020×4038+20192.
=(2020-2019)2=1.
解:(1)原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1=-395;
(2)原式=20202-2×2020×2019+20192
小试牛刀
3、
已知x-y=5,xy=-4.求:
(1)
x2+y2的值(2)(x+y)2的值.
=25-8=17;
解:(1)∵x-y=5,xy=-4,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=17,xy=-4,
∴(x+y)2=x2+y2+2xy
=17-8=9.
知识点拨:本题要熟练掌握完全平方公式的变式:
x2+y2=(x-y)2+2xy=(x+y)2-2xy,(x-y)2=(x+y)2-4xy.
回顾旧知
a+(b+c)
=
a+b+c;
a-(b+c)
=
a–b–c.
a
+
b
+
c
=
a
+
(
b
+
c)
;
a–b–c
=
a
–
(
b
+
c
)
.
去括号法则:
把上面两个等式的左右两边反过来,也就添括号:
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则:
典例精析
例3
、运用乘法公式计算:
(1)
(x+2y-3)(x-2y+3)
;
(2)
(a+b+c)2.
原式=[x+(2y–3)][x-(2y-3)]
解:
(1)
(2)原式
=
[(a+b)+c]2
=
x2-(2y-3)2
=
x2-(4y2-12y+9)
=
x2-4y2+12y-9.
=
(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
针对训练
计算:(1)(a+2b-1)2;
(2)(2x+y+z)(2x-y-z).
=4x2-y2-2yz-z2
解:(1)原式=[(a+2b)-1]2
=(a+2b)2-2(a+2b)
+12
=a2+2ab+b2-2a-4b+1
(2)原式=[2x+(y+z)][2x-(y+z)]
=4x2-(y+z)2
课堂总结
今天我们收获了哪些知识?
1.说一说乘法的完全平方公式?
2.应用完全平方公式时要注意什么?
(a
±
b)2=
a2
±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
综合演练
C
1.计算(-a-b)2的结果是(
)
A.a2+b2
B.a2-b2
C.a2+2ab+b2
D.a2-2ab+b2
知识点拨:
(a+b)2
与(-a-b)2
相等。
2.下列计算结果为2ab-a2-b2的是(
)
A.(a-b)2
B.(-a-b)2
C.-(a+b)2
D.-(a-b)2
D
知识点拨:完全平方公式的逆运算,注意符号。
综合演练
3.下列添括号错误的是(
)
A.a2-b2-b+a=a2-b2+(a-b)
B.(a+b+c)(a-b-c)=[a+(b+c)][a-(b+c)]
C.a-b+c-d=(a-d)+(c-b)
D.a-b=-(b+a)
D
知识点拨:添加括号时,负变正不变。
综合演练
4、已知
则
_____
98
5、如果x2+kx+81是运用完全平方式得到的结果,则k=______
8或-8
6、如果x2+6x+m2是完全平方式,则m的值是_____
3或-3
综合演练
7.已知(a+b+1)(a+b-1)=63,求a+b的值.
解:∵
(a+b+1)(a+b-1)=63
[(a+b)+1][(a+b)-1]=63
∴(a+b)2-1=63
∴(a+b)2=64
∴a+b=±8
综合演练
8.若a+b=5,ab=-6,
求a2+b2,a2-ab+b2.
解:a2+b2
=(a+b)2-2ab
=52-2×(-6)
=37;
a2-ab+b2
=a2+b2-ab
=37-(-6)
=43.
课后作业
教材112页练习题第2、3题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
14.2.2完全平方公式
学习目标
1.理解并掌握完全平方公式的推导过程、结构特点、
几何解释.(重点)
2.灵活应用完全平方公式进行计算.(难点)
回顾旧知
2.填空:
1.说一说乘法的平方差公式?
两个数的和与这两个数的差的积,等于这两个数的平方差.
合作探究
思考1:
计算下列多项式的积,你能发现什么规律?
思考2:
根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2=
.
a2+2ab+b2
(a-b)2=
.
a2-2ab+b2
合作探究
完全平方公式:
(a+b)2=
.
a2+2ab+b2
(a-b)2=
.
a2-2ab+b2
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为:
“首平方,尾平方,积的2倍放中间”
合作探究
思考3:你能根据下图中的面积说明完全平方公式吗?
合作探究
合作探究
合作探究
(a+b)2=
a2+2ab+b2.
(a-b)2=a2-2ab+b2.
思考4:观察下面两个完全平方式,比一比,回答下列问题:
1.说一说积的次数和项数.
2.两个完全平方式的积有相同的项吗?与a,b有什么关系?
3.两个完全平方式的积中不同的是哪一项?与
a,b有什么关系?它的符号与什么有关?
合作探究
公式特征:
3.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和,另一项是两数积的2倍,且与两数中
间的符号相同
;
针对训练
1、下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(a+b)2=a2
+b2
(2)(a-b)2
=a2
–ab+b2
(3)
(-x
+y)2
=x2+2xy
+y2
(4)
(2x+y)2
=4x2
+2xy
+y2
×
×
×
×
(a
+b)2
=a2+2ab
+b2
(a
-b)2
=a2
-2ab
+b2
(-x
+y)2
=x2
-2xy
+y2
(2x
+y)2
=4x2+4xy
+y2
典例精析
例1.用完全平方公式计算:
解:
典例精析
(1)
1022;
解:
1022
=
(100+2)2
=10000+400+4
=10404.
(2)
992.
992
=
(100
–1)2
=10000
-200+1
=9801.
例2
运用完全平方公式计算:
知识点拨:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
小试牛刀
1、利用完全平方公式计算:
(1)(x+6)2;
(2)(-3m-4n)2;
(3)(-3a+b)2.
(3)(-3a+b)2=9a2-6ab+b2.
解:(1)(x+6)2=x2+12x+36;
(2)(-3m-4n)2=9m2+24mn+16n2;
那
(-x-6)2呢?
它与(b-3a)2的值相等吗?
知识点拨:
(a+b)2
与(-a-b)2
相等,
(a-b)2
与(b-a)2相等。
(a-b)2与a2-b2值相等吗?为什么?
小试牛刀
2、利用乘法公式计算:
(1)982-101×99;
(2)20202-2020×4038+20192.
=(2020-2019)2=1.
解:(1)原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1=-395;
(2)原式=20202-2×2020×2019+20192
小试牛刀
3、
已知x-y=5,xy=-4.求:
(1)
x2+y2的值(2)(x+y)2的值.
=25-8=17;
解:(1)∵x-y=5,xy=-4,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=17,xy=-4,
∴(x+y)2=x2+y2+2xy
=17-8=9.
知识点拨:本题要熟练掌握完全平方公式的变式:
x2+y2=(x-y)2+2xy=(x+y)2-2xy,(x-y)2=(x+y)2-4xy.
回顾旧知
a+(b+c)
=
a+b+c;
a-(b+c)
=
a–b–c.
a
+
b
+
c
=
a
+
(
b
+
c)
;
a–b–c
=
a
–
(
b
+
c
)
.
去括号法则:
把上面两个等式的左右两边反过来,也就添括号:
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则:
典例精析
例3
、运用乘法公式计算:
(1)
(x+2y-3)(x-2y+3)
;
(2)
(a+b+c)2.
原式=[x+(2y–3)][x-(2y-3)]
解:
(1)
(2)原式
=
[(a+b)+c]2
=
x2-(2y-3)2
=
x2-(4y2-12y+9)
=
x2-4y2+12y-9.
=
(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
针对训练
计算:(1)(a+2b-1)2;
(2)(2x+y+z)(2x-y-z).
=4x2-y2-2yz-z2
解:(1)原式=[(a+2b)-1]2
=(a+2b)2-2(a+2b)
+12
=a2+2ab+b2-2a-4b+1
(2)原式=[2x+(y+z)][2x-(y+z)]
=4x2-(y+z)2
课堂总结
今天我们收获了哪些知识?
1.说一说乘法的完全平方公式?
2.应用完全平方公式时要注意什么?
(a
±
b)2=
a2
±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
综合演练
C
1.计算(-a-b)2的结果是(
)
A.a2+b2
B.a2-b2
C.a2+2ab+b2
D.a2-2ab+b2
知识点拨:
(a+b)2
与(-a-b)2
相等。
2.下列计算结果为2ab-a2-b2的是(
)
A.(a-b)2
B.(-a-b)2
C.-(a+b)2
D.-(a-b)2
D
知识点拨:完全平方公式的逆运算,注意符号。
综合演练
3.下列添括号错误的是(
)
A.a2-b2-b+a=a2-b2+(a-b)
B.(a+b+c)(a-b-c)=[a+(b+c)][a-(b+c)]
C.a-b+c-d=(a-d)+(c-b)
D.a-b=-(b+a)
D
知识点拨:添加括号时,负变正不变。
综合演练
4、已知
则
_____
98
5、如果x2+kx+81是运用完全平方式得到的结果,则k=______
8或-8
6、如果x2+6x+m2是完全平方式,则m的值是_____
3或-3
综合演练
7.已知(a+b+1)(a+b-1)=63,求a+b的值.
解:∵
(a+b+1)(a+b-1)=63
[(a+b)+1][(a+b)-1]=63
∴(a+b)2-1=63
∴(a+b)2=64
∴a+b=±8
综合演练
8.若a+b=5,ab=-6,
求a2+b2,a2-ab+b2.
解:a2+b2
=(a+b)2-2ab
=52-2×(-6)
=37;
a2-ab+b2
=a2+b2-ab
=37-(-6)
=43.
课后作业
教材112页练习题第2、3题.
https://www.21cnjy.com/help/help_extract.php
