五年级上册数学课件-6.1 因数和倍数青岛版 (共21张PPT)
文档属性
| 名称 | 五年级上册数学课件-6.1 因数和倍数青岛版 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 549.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 11:58:50 | ||
图片预览







文档简介
(共21张PPT)
因数和倍数
你能提出什么问题?
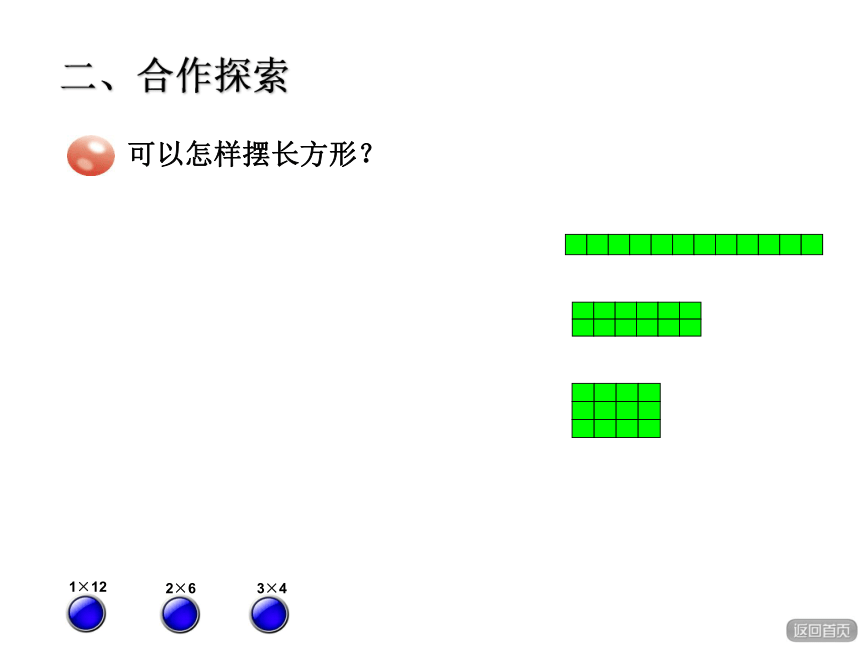
二、合作探索
可以怎样摆长方形?
1×12
2×6
3×4
二、合作探索
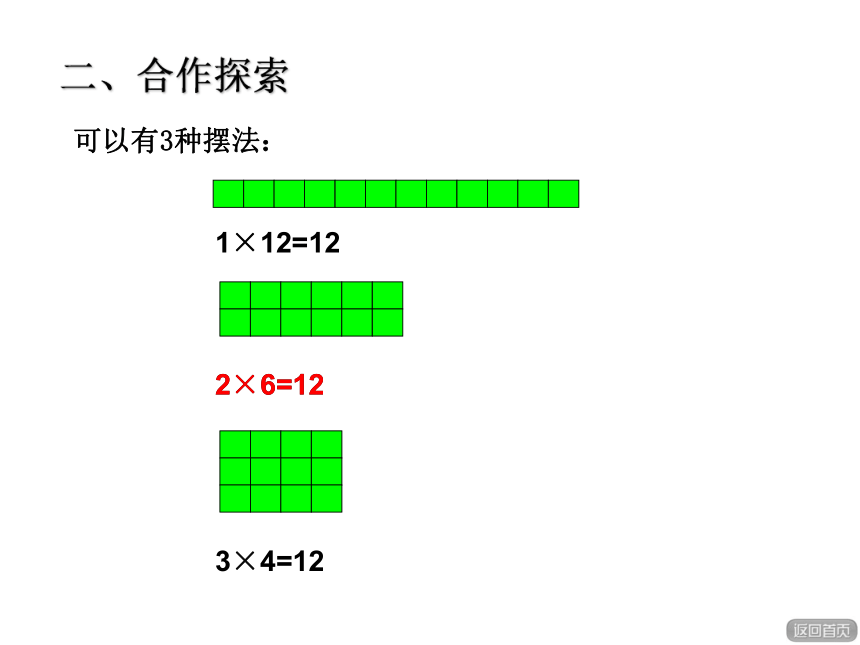
1×12=12
2×6=12
3×4=12
2×6=12
可以有3种摆法:
二、合作探索
2
×
6
=
12
是
的因数
是
的因数
是
的倍数
是
的倍数
2
12
12
2
12
12
6
6
在研究因数和倍数时,我们所指的数是自然数(不包括0)。
32÷4=8,你能从这个算式中找到因数和倍数吗?
32是4的倍数
4是32的因数
32是8的倍数
8是32的因数
试一试
根据下面的算式,说一说谁是谁的因数,谁是谁的倍数。
7×6=42
56÷8=7
7和6都是42的因数,42既是7的倍数也是6的倍数。
8和7都是56的因数,56既是8的倍数也是7的倍数。
因为2
×
4=8,所以
8是倍数,4是因数。
……
……
(
)
×
8是4的倍数,4是8的因数。
判断
二、合作探究
想一想,怎样找才能做到既不重复又不遗漏找出24的所有因数呢?试试看!
二、合作探索
想一想,怎样找,才能既不重复,又不遗漏地找出24的因数?
24的因数有:
4
6
24
8
2
1
24
24
1
2
8
6
4
12
×
=
24
×
=
24
3
×
=
×
=
3
12
24
依次一对一对地找,既不重复,也不遗漏。
返回
试一试:你能用我们找到的方法找出16的因数吗?
()×()=16
()×()=16
()×()=16
16的因数有:——————————————
4
2
1
16
16
1
2
4
8
×
=
16
×
=
16
4
×
=
4
16的因数有:
8
16
试一试
你能用我们找到的方法找出16的因数吗?
1
16
2
8
4
4
重复的只保留一个。
12的因数有:
2,
3,
4,
6,
24的因数有:
2,
3,
4,6,
8,
12,
16的因数有:
2,4,
8,
1,
1,
1,
12
24
16
一个数的因数的特征
1
它本身
有限的
二、合作探索
一个数的因数有哪些特征呢?
最小的因数
最大的因数
一个数的因数的个数
你能找出3的倍数吗?
3的倍数有:
3
×
1
=
3
×
2
=
3
×
3
=
3
×
4
=
3
×
5
=
3
6
9
12
15
……
3,
6,
9,
12,
15
……
3乘非零自然数的积就是3的倍数。
2的倍数有:
2,
试一试:
5的倍数有:
4,
6,
8,
……
5,
10,
15,
20,
25
……
10
3的倍数有:
2的倍数有:
5的倍数有:
……
3
一个数的倍数的特征
这个数的本身
没有
二、合作探索
一个数的倍数有哪些特征呢?
6
9
12
2
4
6
8
5
10
15
20
……
……
无限的
最小的倍数
最大的倍数
一个数的倍数的个数
基本练习
下列说法对吗?为什么?
(1)一个数的倍数一定比这个数的因数大。
(
)
(2)2.8是7的倍数。
(
)
(3)因为42÷7=6,所以42是7的倍数。
(
)
(4)一个数的因数的个数是有限的,而它的倍数的个数是无限的。
(
)
√
×
×
√
基本练习
50以内8的倍数有哪些?
8、16、24、32、40、48
拓展延伸
小明和小红分别用20个和49个1平方厘米的小正方形拼摆长方形,谁的摆法多?为什么?
稀少而有趣的完美数
任何一个自然数的因数中都有1和它本身,我们把小于它本身的因数叫做这个自然数的真因数。如6的所有真因数是1、2、3,而且6=1+2+3,像这样的数,数学家们叫它完美数。
古希腊人非常重视完美数。古希腊著名的数学家毕达哥拉斯发现它之后,人们就开始了对完美数的研究。也许完美数太少了,一直到现在,数学家才发现了29个完美数,而且都是偶完美数。前5个完美数分别是:6,
28,
496,
8128,33550336。
你有什么收获?
因数和倍数
你能提出什么问题?
二、合作探索
可以怎样摆长方形?
1×12
2×6
3×4
二、合作探索
1×12=12
2×6=12
3×4=12
2×6=12
可以有3种摆法:
二、合作探索
2
×
6
=
12
是
的因数
是
的因数
是
的倍数
是
的倍数
2
12
12
2
12
12
6
6
在研究因数和倍数时,我们所指的数是自然数(不包括0)。
32÷4=8,你能从这个算式中找到因数和倍数吗?
32是4的倍数
4是32的因数
32是8的倍数
8是32的因数
试一试
根据下面的算式,说一说谁是谁的因数,谁是谁的倍数。
7×6=42
56÷8=7
7和6都是42的因数,42既是7的倍数也是6的倍数。
8和7都是56的因数,56既是8的倍数也是7的倍数。
因为2
×
4=8,所以
8是倍数,4是因数。
……
……
(
)
×
8是4的倍数,4是8的因数。
判断
二、合作探究
想一想,怎样找才能做到既不重复又不遗漏找出24的所有因数呢?试试看!
二、合作探索
想一想,怎样找,才能既不重复,又不遗漏地找出24的因数?
24的因数有:
4
6
24
8
2
1
24
24
1
2
8
6
4
12
×
=
24
×
=
24
3
×
=
×
=
3
12
24
依次一对一对地找,既不重复,也不遗漏。
返回
试一试:你能用我们找到的方法找出16的因数吗?
()×()=16
()×()=16
()×()=16
16的因数有:——————————————
4
2
1
16
16
1
2
4
8
×
=
16
×
=
16
4
×
=
4
16的因数有:
8
16
试一试
你能用我们找到的方法找出16的因数吗?
1
16
2
8
4
4
重复的只保留一个。
12的因数有:
2,
3,
4,
6,
24的因数有:
2,
3,
4,6,
8,
12,
16的因数有:
2,4,
8,
1,
1,
1,
12
24
16
一个数的因数的特征
1
它本身
有限的
二、合作探索
一个数的因数有哪些特征呢?
最小的因数
最大的因数
一个数的因数的个数
你能找出3的倍数吗?
3的倍数有:
3
×
1
=
3
×
2
=
3
×
3
=
3
×
4
=
3
×
5
=
3
6
9
12
15
……
3,
6,
9,
12,
15
……
3乘非零自然数的积就是3的倍数。
2的倍数有:
2,
试一试:
5的倍数有:
4,
6,
8,
……
5,
10,
15,
20,
25
……
10
3的倍数有:
2的倍数有:
5的倍数有:
……
3
一个数的倍数的特征
这个数的本身
没有
二、合作探索
一个数的倍数有哪些特征呢?
6
9
12
2
4
6
8
5
10
15
20
……
……
无限的
最小的倍数
最大的倍数
一个数的倍数的个数
基本练习
下列说法对吗?为什么?
(1)一个数的倍数一定比这个数的因数大。
(
)
(2)2.8是7的倍数。
(
)
(3)因为42÷7=6,所以42是7的倍数。
(
)
(4)一个数的因数的个数是有限的,而它的倍数的个数是无限的。
(
)
√
×
×
√
基本练习
50以内8的倍数有哪些?
8、16、24、32、40、48
拓展延伸
小明和小红分别用20个和49个1平方厘米的小正方形拼摆长方形,谁的摆法多?为什么?
稀少而有趣的完美数
任何一个自然数的因数中都有1和它本身,我们把小于它本身的因数叫做这个自然数的真因数。如6的所有真因数是1、2、3,而且6=1+2+3,像这样的数,数学家们叫它完美数。
古希腊人非常重视完美数。古希腊著名的数学家毕达哥拉斯发现它之后,人们就开始了对完美数的研究。也许完美数太少了,一直到现在,数学家才发现了29个完美数,而且都是偶完美数。前5个完美数分别是:6,
28,
496,
8128,33550336。
你有什么收获?
