苏科版八年级数学上册1.1 全等图形同步练习(Word版 含解析)
文档属性
| 名称 | 苏科版八年级数学上册1.1 全等图形同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 00:00:00 | ||
图片预览


文档简介
1.1
全等图形
一.选择题(共10小题)
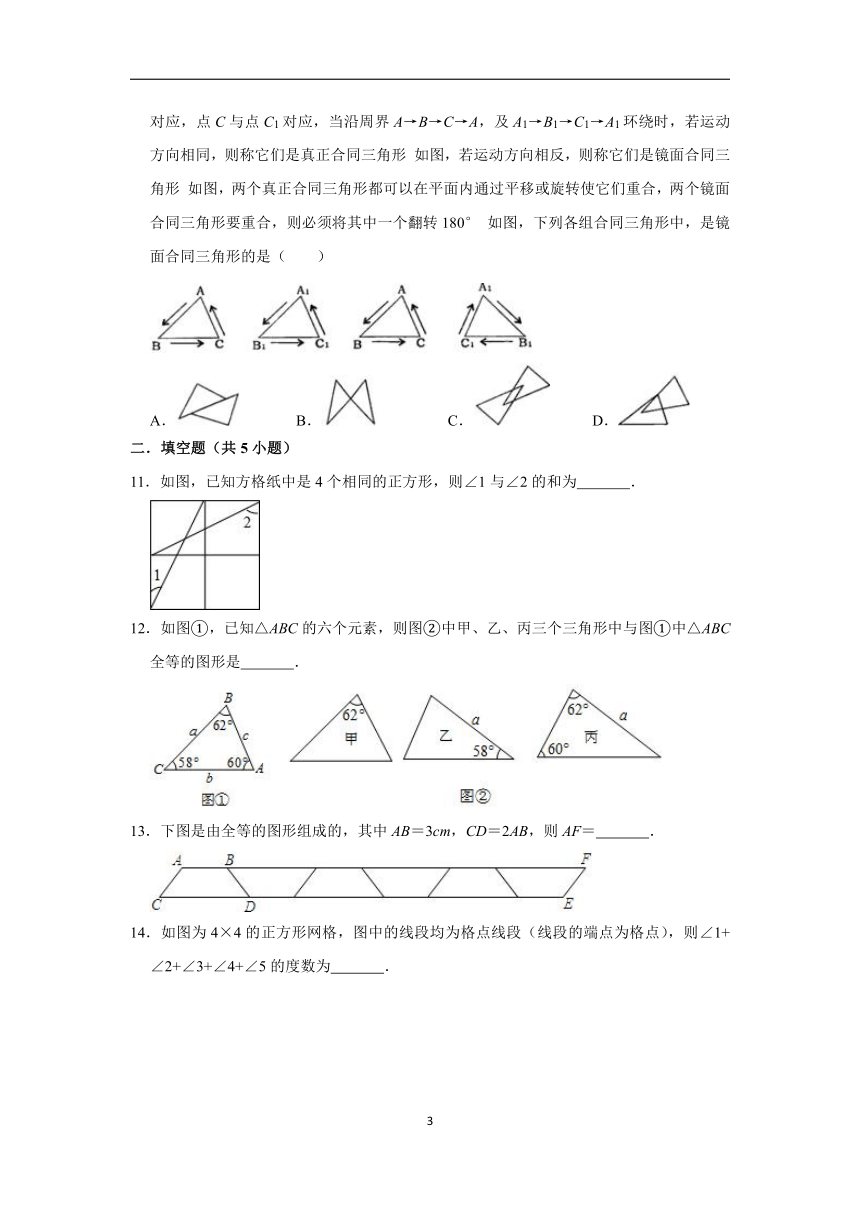
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
2.如图所示的图形是全等图形的是( )
A.
B.
C.
D.
3.下列各组的两个图形属于全等图形的是
( )
A.
B.
C.
D.
4.下列选项中表示两个全等图形的是( )
A.形状相同的两个图形
B.能够完全重合的两个图形
C.面积相等的两个图形
D.周长相等的两个图形
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90°
B.105°
C.120°
D.135°
6.下列四个选项中的图形与最左边的图形全等的是( )
A.
B.
C.
D.
7.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(
1
)(
3)(
4
)
B.(
2)(
3
)(
4
)
C.(
1
)(
2
)(
3
)
D.(
1
)(
2)(
3
)(
4
)
8.下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.②和④
9.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
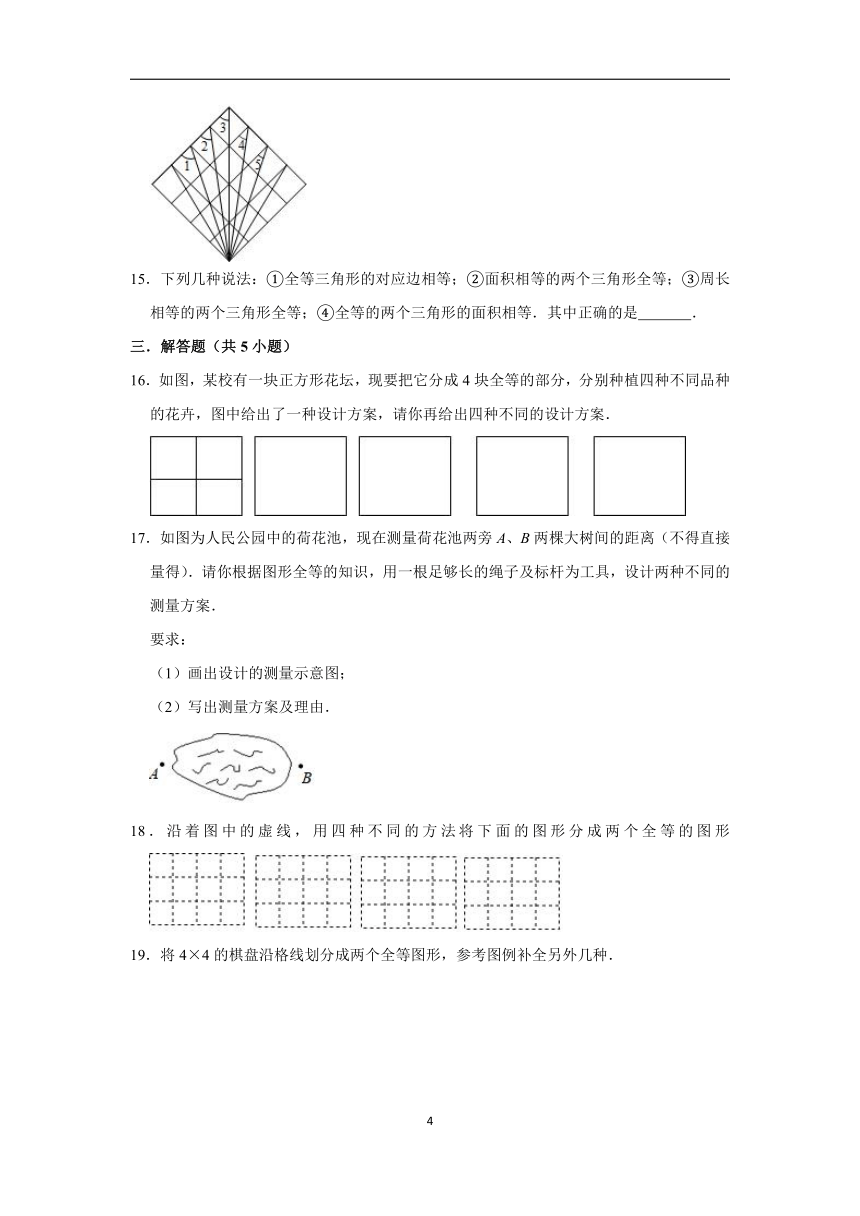
10.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形
如图,若运动方向相反,则称它们是镜面合同三角形
如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°
如图,下列各组合同三角形中,是镜面合同三角形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
11.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为
.
12.如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是
.
13.下图是由全等的图形组成的,其中AB=3cm,CD=2AB,则AF=
.
14.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为
.
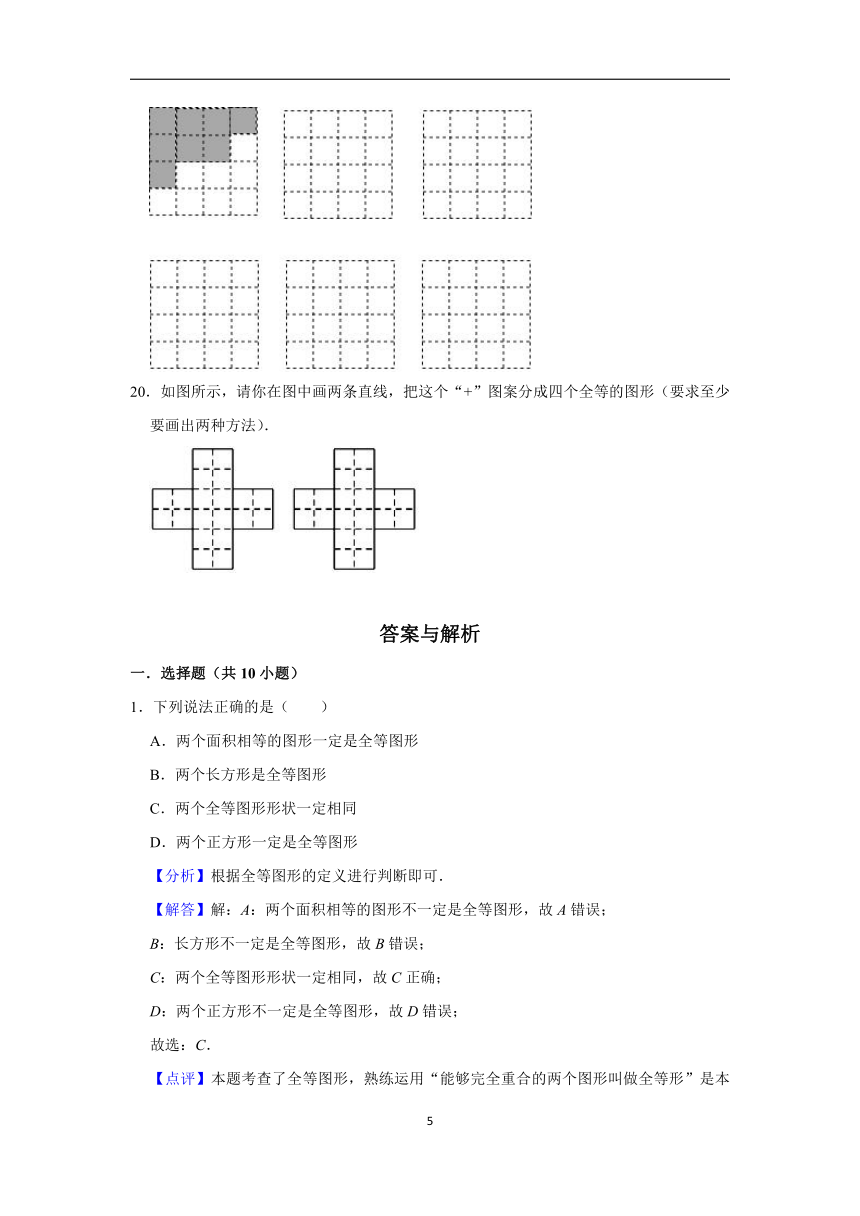
15.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是
.
三.解答题(共5小题)
16.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
17.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
18.沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
答案与解析
一.选择题(共10小题)
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
【分析】根据全等图形的定义进行判断即可.
【解答】解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
【点评】本题考查了全等图形,熟练运用“能够完全重合的两个图形叫做全等形”是本题的关键.
2.如图所示的图形是全等图形的是( )
A.
B.
C.
D.
【分析】根据能够完全重合的两个图形叫做全等形可得答案.
【解答】解:如图所示的图形是全等图形的是B,
故选:B.
【点评】此题主要考查了全等图形,关键是掌握全等形的定义.
3.下列各组的两个图形属于全等图形的是
( )
A.
B.
C.
D.
【分析】根据全等形是能够完全重合的两个图形进行分析判断.
【解答】解:A、两只眼睛下面的嘴巴不能完全重合,故本选项错误;
B、两个正方形的边长不相等,不能完全重合,故本选项错误;
C、圆内两条相交的线段不能完全重合,故本选项错误;
D、两个图形能够完全重合,故本选项正确.
故选:D.
【点评】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
4.下列选项中表示两个全等图形的是( )
A.形状相同的两个图形
B.能够完全重合的两个图形
C.面积相等的两个图形
D.周长相等的两个图形
【分析】直接利用全等图形的定义分析得出答案.
【解答】解:A、形状相同的两个图形,不一定是全等图形,故此选项错误;
B、能够完全重合的两个图形,一定是全等图形,故此选项正确;
C、面积相等的两个图形,不一定是全等图形,故此选项错误;
D、周长相等的两个图形,不一定是全等图形,故此选项错误;
故选:B.
【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90°
B.105°
C.120°
D.135°
【分析】根据对称性可得∠1+∠3=90°,∠2=45°.
【解答】解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,
∴∠1+∠3=90°,
又∠2=45°,
∴∠1+∠2+∠3=135°,
故选:D.
【点评】主要考查了正方形的性质和全等三角形的判定.充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题.
6.下列四个选项中的图形与最左边的图形全等的是( )
A.
B.
C.
D.
【分析】根据全等图形判断即可.
【解答】解:只有B选项的图形与已知图形全等,
故选:B.
【点评】此题考查全等图形问题,关键根据全等图形的定义判断.
7.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(
1
)(
3)(
4
)
B.(
2)(
3
)(
4
)
C.(
1
)(
2
)(
3
)
D.(
1
)(
2)(
3
)(
4
)
【分析】能够完全重合的两个三角形叫做全等三角形,依据全等三角形的性质,即可得到正确结论.
【解答】解:(1)全等图形的形状相同,大小相等,正确;
(2)全等三角形的对应边相等,正确;
(3)全等图形的周长相等,面积相等,正确;
(4)面积相等的两个三角形不一定全等,错误;
故选:C.
【点评】本题主要考查了全等三角形的性质,解题时注意:能够完全重合的两个图形叫做全等形.
8.下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.②和④
【分析】根据全等形的概念:能够完全重合的两个图形叫做全等形可得答案.
【解答】解:②和④都可以完全重合,因此全等的图形是②和④.
故选:D.
【点评】此题主要考查了全等图形,关键是掌握全等图形的概念.
9.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
【分析】根据两个三角形全等,可以得到3对三角形的边相等,根据BC=EF,又可以得到BE=CF可得答案是4对.
【解答】解:∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF
∵BC=EF,即BE+EC=CF+EC
∴BE=CF
即有4对相等的线段
故选:D.
【点评】本题主要考查了全等三角形的对应边相等问题;做题时,结合已知,认真观察图形,得到BE=CF是正确解答本题的关键.
10.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形
如图,若运动方向相反,则称它们是镜面合同三角形
如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°
如图,下列各组合同三角形中,是镜面合同三角形的是( )
A.
B.
C.
D.
【分析】认真阅读题目,理解真正合同三角形和镜面合同三角形的定义,然后根据各自的定义或特点进行解答.
【解答】解:由题意知真正合同三角形和镜面合同三角形的特点,可判断要使选项B的两个三角形重合必须将其中的一个翻转180°;
而其A、D、C的全等三角形可以在平面内通过平移或旋转使它们重合.
故选:B.
【点评】此题考查了全等图形的知识,学生要注意阅读理解能力及空间想象能力的培养,题目出的较灵活,认真读题,透彻理解题意是正确解决本题的关键.
二.填空题(共5小题)
11.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为 90° .
【分析】首先证明△ABC≌△AED,根据全等三角形的性质可得∠1=∠AED,再根据余角的定义可得∠AED+∠2=90°,再根据等量代换可得∠1与∠2的和为90°.
【解答】解:∵在△ABC和△AED中
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,
故答案为:90°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定和性质.
12.如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是 丙 .
【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
【解答】解:已知图①的△ABC中,∠B=62°,BC=a,AB=c,AC=b,∠C=58°,∠A=60°,
图②中,甲:只有一个角和∠B相等,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
乙:只有一个角和∠B相等,还有一条边,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
丙:符合AAS定理,能推出两三角形全等;
故答案为:丙.
【点评】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
13.下图是由全等的图形组成的,其中AB=3cm,CD=2AB,则AF= 27cm .
【分析】根据已知图形得出CD=2AB=6cm,进而求出即可.
【解答】解:因为AB=3cm,所以CD=2AB=6cm,
所以AF=3AB+3CD=3×3+3×6=27(cm).
故答案为:27cm.
【点评】此题主要考查了全等图形的性质,得出CD的长是解题关键.
14.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 225° .
【分析】根据正方形的性质可得出∠3=45°,根据长方形的性质即可得出相等的边,由此可得出全等的三角形,进而得出∠1与∠5互余、∠2与∠4互余,再将其代入∠1+∠2+∠3+∠4+∠5中即可得出结论.
【解答】解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
【点评】本题考查了全等图形、全等三角形的判定与性质、长方形及正方形的性质,解题的关键是找出∠3=45°、∠1与∠5互余、∠2与∠4互余.
15.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是 ①④ .
【分析】根据全等三角形:能够完全重合的两个三角形叫做全等三角形可得①④正确,但是面积相等或周长相等的两个三角形却不一定全等.
【解答】解:①全等三角形的对应边相等,说法正确;
②面积相等的两个三角形全等,说法错误;
③周长相等的两个三角形全等,说法错误;
④全等的两个三角形的面积相等,说法正确;
故答案为:①④.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
三.解答题(共10小题)
16.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
【分析】根据正方形的性质,①两条对角线把正方形分成四个全等的三角形;②作一组对边的平行线也能把正方形分成四个全等的矩形;③连接一组对边的中点,把正方形分成两个全等的矩形,再作矩形的对角线就把每个矩形都分成两个全等的三角形,这样就分成了四个全等的三角形;④过正方形的中心做互相垂直的两条线也能把正方形分成四个全等的四边形.
【解答】解:设计方案如下:
【点评】本题主要考查了全等图形的意义,要利用正方形及全等形的性质解答,方案多种多样,只要是满足要求就可以.
17.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
【分析】(1)本题属于主观性试题,有多种方案,我们可以构造8字形的全等三角形来测得揽月湖的长度(如下图);
(2)根据三角形全等的证明得出对应边相等即可得出答案.
【解答】解:(1)如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
【点评】此题考查了全等三角形的应用与证明;此题带有一定主观性,学生要根据已知知识对新问题进行探索和对基础知识进行巩固,这种做法较常见,要熟练掌握.
18.沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形
【分析】直接利用图形形状分成全等的两部分即可.
【解答】解:如图所示:
.
【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
【分析】能够完全重合的两个图形叫做全等形,可以利用图形的轴对称性和中心对称性来分割成两个全等的图形.
【解答】解:如图所示,(答案不唯一)
【点评】本题主要考查了全等图形,解题的关键是掌握全等图形的定义:形状和大小完全相同的两个图形叫全等形.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
【分析】根据能够完全重合的两个图形叫做全等形画线即可.
【解答】解:如图所示:
.
【点评】此题主要考查了全等图形,关键是掌握全等图形的概念.
1
全等图形
一.选择题(共10小题)
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
2.如图所示的图形是全等图形的是( )
A.
B.
C.
D.
3.下列各组的两个图形属于全等图形的是
( )
A.
B.
C.
D.
4.下列选项中表示两个全等图形的是( )
A.形状相同的两个图形
B.能够完全重合的两个图形
C.面积相等的两个图形
D.周长相等的两个图形
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90°
B.105°
C.120°
D.135°
6.下列四个选项中的图形与最左边的图形全等的是( )
A.
B.
C.
D.
7.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(
1
)(
3)(
4
)
B.(
2)(
3
)(
4
)
C.(
1
)(
2
)(
3
)
D.(
1
)(
2)(
3
)(
4
)
8.下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.②和④
9.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
10.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形
如图,若运动方向相反,则称它们是镜面合同三角形
如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°
如图,下列各组合同三角形中,是镜面合同三角形的是( )
A.
B.
C.
D.
二.填空题(共5小题)
11.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为
.
12.如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是
.
13.下图是由全等的图形组成的,其中AB=3cm,CD=2AB,则AF=
.
14.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为
.
15.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是
.
三.解答题(共5小题)
16.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
17.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
18.沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
答案与解析
一.选择题(共10小题)
1.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
【分析】根据全等图形的定义进行判断即可.
【解答】解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
【点评】本题考查了全等图形,熟练运用“能够完全重合的两个图形叫做全等形”是本题的关键.
2.如图所示的图形是全等图形的是( )
A.
B.
C.
D.
【分析】根据能够完全重合的两个图形叫做全等形可得答案.
【解答】解:如图所示的图形是全等图形的是B,
故选:B.
【点评】此题主要考查了全等图形,关键是掌握全等形的定义.
3.下列各组的两个图形属于全等图形的是
( )
A.
B.
C.
D.
【分析】根据全等形是能够完全重合的两个图形进行分析判断.
【解答】解:A、两只眼睛下面的嘴巴不能完全重合,故本选项错误;
B、两个正方形的边长不相等,不能完全重合,故本选项错误;
C、圆内两条相交的线段不能完全重合,故本选项错误;
D、两个图形能够完全重合,故本选项正确.
故选:D.
【点评】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
4.下列选项中表示两个全等图形的是( )
A.形状相同的两个图形
B.能够完全重合的两个图形
C.面积相等的两个图形
D.周长相等的两个图形
【分析】直接利用全等图形的定义分析得出答案.
【解答】解:A、形状相同的两个图形,不一定是全等图形,故此选项错误;
B、能够完全重合的两个图形,一定是全等图形,故此选项正确;
C、面积相等的两个图形,不一定是全等图形,故此选项错误;
D、周长相等的两个图形,不一定是全等图形,故此选项错误;
故选:B.
【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90°
B.105°
C.120°
D.135°
【分析】根据对称性可得∠1+∠3=90°,∠2=45°.
【解答】解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,
∴∠1+∠3=90°,
又∠2=45°,
∴∠1+∠2+∠3=135°,
故选:D.
【点评】主要考查了正方形的性质和全等三角形的判定.充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题.
6.下列四个选项中的图形与最左边的图形全等的是( )
A.
B.
C.
D.
【分析】根据全等图形判断即可.
【解答】解:只有B选项的图形与已知图形全等,
故选:B.
【点评】此题考查全等图形问题,关键根据全等图形的定义判断.
7.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )
A.(
1
)(
3)(
4
)
B.(
2)(
3
)(
4
)
C.(
1
)(
2
)(
3
)
D.(
1
)(
2)(
3
)(
4
)
【分析】能够完全重合的两个三角形叫做全等三角形,依据全等三角形的性质,即可得到正确结论.
【解答】解:(1)全等图形的形状相同,大小相等,正确;
(2)全等三角形的对应边相等,正确;
(3)全等图形的周长相等,面积相等,正确;
(4)面积相等的两个三角形不一定全等,错误;
故选:C.
【点评】本题主要考查了全等三角形的性质,解题时注意:能够完全重合的两个图形叫做全等形.
8.下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.②和④
【分析】根据全等形的概念:能够完全重合的两个图形叫做全等形可得答案.
【解答】解:②和④都可以完全重合,因此全等的图形是②和④.
故选:D.
【点评】此题主要考查了全等图形,关键是掌握全等图形的概念.
9.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
【分析】根据两个三角形全等,可以得到3对三角形的边相等,根据BC=EF,又可以得到BE=CF可得答案是4对.
【解答】解:∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF
∵BC=EF,即BE+EC=CF+EC
∴BE=CF
即有4对相等的线段
故选:D.
【点评】本题主要考查了全等三角形的对应边相等问题;做题时,结合已知,认真观察图形,得到BE=CF是正确解答本题的关键.
10.全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形
如图,若运动方向相反,则称它们是镜面合同三角形
如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°
如图,下列各组合同三角形中,是镜面合同三角形的是( )
A.
B.
C.
D.
【分析】认真阅读题目,理解真正合同三角形和镜面合同三角形的定义,然后根据各自的定义或特点进行解答.
【解答】解:由题意知真正合同三角形和镜面合同三角形的特点,可判断要使选项B的两个三角形重合必须将其中的一个翻转180°;
而其A、D、C的全等三角形可以在平面内通过平移或旋转使它们重合.
故选:B.
【点评】此题考查了全等图形的知识,学生要注意阅读理解能力及空间想象能力的培养,题目出的较灵活,认真读题,透彻理解题意是正确解决本题的关键.
二.填空题(共5小题)
11.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为 90° .
【分析】首先证明△ABC≌△AED,根据全等三角形的性质可得∠1=∠AED,再根据余角的定义可得∠AED+∠2=90°,再根据等量代换可得∠1与∠2的和为90°.
【解答】解:∵在△ABC和△AED中
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,
故答案为:90°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定和性质.
12.如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是 丙 .
【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
【解答】解:已知图①的△ABC中,∠B=62°,BC=a,AB=c,AC=b,∠C=58°,∠A=60°,
图②中,甲:只有一个角和∠B相等,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
乙:只有一个角和∠B相等,还有一条边,没有其它条件,不符合三角形全等的判定定理,即和△ABC不全等;
丙:符合AAS定理,能推出两三角形全等;
故答案为:丙.
【点评】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
13.下图是由全等的图形组成的,其中AB=3cm,CD=2AB,则AF= 27cm .
【分析】根据已知图形得出CD=2AB=6cm,进而求出即可.
【解答】解:因为AB=3cm,所以CD=2AB=6cm,
所以AF=3AB+3CD=3×3+3×6=27(cm).
故答案为:27cm.
【点评】此题主要考查了全等图形的性质,得出CD的长是解题关键.
14.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为 225° .
【分析】根据正方形的性质可得出∠3=45°,根据长方形的性质即可得出相等的边,由此可得出全等的三角形,进而得出∠1与∠5互余、∠2与∠4互余,再将其代入∠1+∠2+∠3+∠4+∠5中即可得出结论.
【解答】解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
【点评】本题考查了全等图形、全等三角形的判定与性质、长方形及正方形的性质,解题的关键是找出∠3=45°、∠1与∠5互余、∠2与∠4互余.
15.下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是 ①④ .
【分析】根据全等三角形:能够完全重合的两个三角形叫做全等三角形可得①④正确,但是面积相等或周长相等的两个三角形却不一定全等.
【解答】解:①全等三角形的对应边相等,说法正确;
②面积相等的两个三角形全等,说法错误;
③周长相等的两个三角形全等,说法错误;
④全等的两个三角形的面积相等,说法正确;
故答案为:①④.
【点评】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.
三.解答题(共10小题)
16.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
【分析】根据正方形的性质,①两条对角线把正方形分成四个全等的三角形;②作一组对边的平行线也能把正方形分成四个全等的矩形;③连接一组对边的中点,把正方形分成两个全等的矩形,再作矩形的对角线就把每个矩形都分成两个全等的三角形,这样就分成了四个全等的三角形;④过正方形的中心做互相垂直的两条线也能把正方形分成四个全等的四边形.
【解答】解:设计方案如下:
【点评】本题主要考查了全等图形的意义,要利用正方形及全等形的性质解答,方案多种多样,只要是满足要求就可以.
17.如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.
要求:
(1)画出设计的测量示意图;
(2)写出测量方案及理由.
【分析】(1)本题属于主观性试题,有多种方案,我们可以构造8字形的全等三角形来测得揽月湖的长度(如下图);
(2)根据三角形全等的证明得出对应边相等即可得出答案.
【解答】解:(1)如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
【点评】此题考查了全等三角形的应用与证明;此题带有一定主观性,学生要根据已知知识对新问题进行探索和对基础知识进行巩固,这种做法较常见,要熟练掌握.
18.沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形
【分析】直接利用图形形状分成全等的两部分即可.
【解答】解:如图所示:
.
【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
【分析】能够完全重合的两个图形叫做全等形,可以利用图形的轴对称性和中心对称性来分割成两个全等的图形.
【解答】解:如图所示,(答案不唯一)
【点评】本题主要考查了全等图形,解题的关键是掌握全等图形的定义:形状和大小完全相同的两个图形叫全等形.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
【分析】根据能够完全重合的两个图形叫做全等形画线即可.
【解答】解:如图所示:
.
【点评】此题主要考查了全等图形,关键是掌握全等图形的概念.
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
