人教版八年级上册数学11.2.1《三角形的内角》课件(共19张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.2.1《三角形的内角》课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 09:16:26 | ||
图片预览





文档简介
(共19张PPT)
第十一章
三角形
11.2
与三角形有关的角
11.2.1
三角形的内角
学习目标
1.能运用平行线的性质证明三角形的内角和定理.
2.熟练利用三角形的内角和及直角三角形两锐角互余、
有两个角互余的三角形是直角三角形的结论解决问题.
情景引入
三角形的三个内角和是多少?
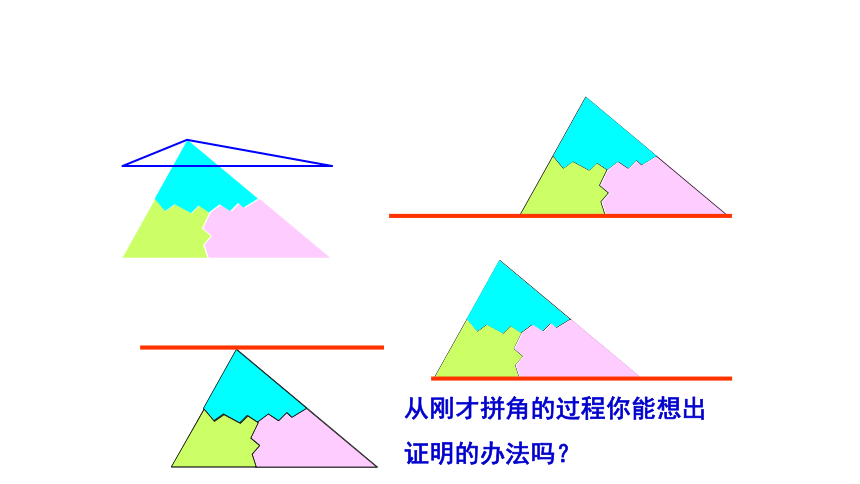
把三角形的三个角拼在一起试试看?
你有什么办法可以验证呢?
180°
从刚才拼角的过程你能想出证明的办法吗?
动手操作
2
1
F
E
C
B
A
已知△ABC,求证∠A+∠B+∠C=180°.
证法1
过A作EF∥BC,
∴∠B=∠2(两直线平行,内错角相等).
∠C=∠1(两直线平行,内错角相等).
又∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
探究新知
2
1
E
D
C
B
A
延长BC
到D,过C作CE∥BA,
∴∠A=∠1(两直线平行,内错角相等).
∠B=∠2(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
已知△ABC,求证∠A+∠B+∠C=180°.
证法2
探究新知
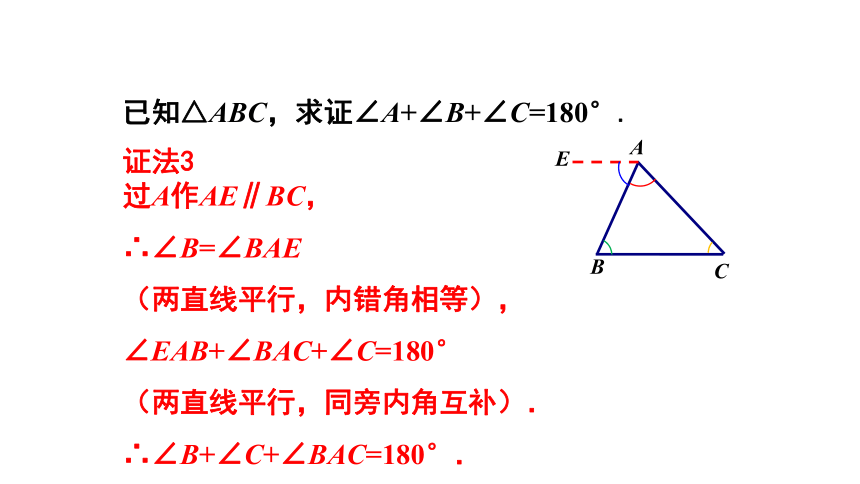
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等),
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补).
∴∠B+∠C+∠BAC=180°.
已知△ABC,求证∠A+∠B+∠C=180°.
证法3
探究新知
E
C
B
A
三角形内角和定理:
三角形三个内角的和等于180°.
探究新知
A
B
C
在直角三角形ABC中,∠C=90°.
由三角形内角和定理,得
∠A+∠B+∠C=180°,
即∠A+∠B+90°=180°,
所以∠A+∠B=90°.
也就是说,直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.
拓展新知
在三角形ABC中,∠A+∠B=90°,
由三角形内角和定理,得,
∠A+∠B+∠C=180°,
即90°+∠C=180°,
所以∠C=90°.
也就是说,有两个角互余的三角形是直角三角形.
拓展新知
A
B
C
A
D
B
C
【例1】如图,在△ABC中,∠BAC=40°,∠B=
75°,AD是△ABC的角平分线.求∠ADB的度数.
分析:要想求出∠ADB的度数,根据三角形内角和定理,只要求出∠DAB的度数即可.由于∠BAC=40°,AD是△ABC的角平分线,所以很容易得出∠DAB=20°.
例题解析
A
D
B
C
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB=
∠BAC=20°,
∵∠B=75°,
∴∠ADB=180°-∠DAB-∠B
=180°-20°-75°
=85°.
例题解析
A
D
B
C
E
北
北
【例2】如图,是A,B,C三岛的平面图,C岛在A岛
的北偏东50°方向,B岛在A岛的北偏东80°方向,
C岛在B岛的北偏西40°方向,从B岛看A,C两岛的
视角∠ABC是多少度?从C岛看A,B两岛的视角
∠ACB是多少度?
分析:怎样求出∠ACB的度数?根据三角形内角和定理,只需求出∠CAB和∠ABC的度数即可.
例题解析
解:∠CAB=∠BAD-∠CAD=80°-50°=30°.
∵AD∥BE,
∴∠BAD+∠ABE=180°.
∴∠ABE=180°-∠BAD=180°-80°=100°.
∴∠ABC=∠ABE-∠EBC=100°-40°=60°.
∴∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°.
答:从B岛看A,C两岛的视角∠ABC是60°,
从C岛看AB两岛的视角∠ACB=90°.
A
D
B
C
E
北
北
例题解析
D
A
B
C
1.已知三角形三个内角的度数之比为1∶3∶5,
求这三个内角的度数.
2.如图,从A处观测C处时仰角∠CAD=30°,从B
处观测C处时仰角∠CBD=45°.从C处观测A,B
两处时视角∠ACB是多少度?
课堂练习
例题解析
1.解:设三个内角度数分别为:x,3x,5x.
列出方程,得x+3x+5x=180°.
解得:x=20°
答:三个内角度数分别为20°,60°,100°
过点C作CF∥AD,
∴∠1=∠DAC=50°,
∵CF∥AD,AD∥BE,
∴CF∥BE.
∴∠2=∠CBE=40°
∴∠ACB=∠1+∠2=50°+40°=90°.
2.你能想出一个更简捷的方法来求∠ACB的度数吗?
1
2
F
A
D
B
C
E
北
北
例题解析
三角形的内角和等于180°.
证法
应用
转化为一个平角或同旁内角互补
求角度
作平行线
转化思想
辅助线
通过本课时的学习,需要我们掌握:
性质:直角三角形的两个锐角互余.
判定:有两个角互余的三角形是直角三角形.
课堂小结
再见
第十一章
三角形
11.2
与三角形有关的角
11.2.1
三角形的内角
学习目标
1.能运用平行线的性质证明三角形的内角和定理.
2.熟练利用三角形的内角和及直角三角形两锐角互余、
有两个角互余的三角形是直角三角形的结论解决问题.
情景引入
三角形的三个内角和是多少?
把三角形的三个角拼在一起试试看?
你有什么办法可以验证呢?
180°
从刚才拼角的过程你能想出证明的办法吗?
动手操作
2
1
F
E
C
B
A
已知△ABC,求证∠A+∠B+∠C=180°.
证法1
过A作EF∥BC,
∴∠B=∠2(两直线平行,内错角相等).
∠C=∠1(两直线平行,内错角相等).
又∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
探究新知
2
1
E
D
C
B
A
延长BC
到D,过C作CE∥BA,
∴∠A=∠1(两直线平行,内错角相等).
∠B=∠2(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
已知△ABC,求证∠A+∠B+∠C=180°.
证法2
探究新知
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等),
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补).
∴∠B+∠C+∠BAC=180°.
已知△ABC,求证∠A+∠B+∠C=180°.
证法3
探究新知
E
C
B
A
三角形内角和定理:
三角形三个内角的和等于180°.
探究新知
A
B
C
在直角三角形ABC中,∠C=90°.
由三角形内角和定理,得
∠A+∠B+∠C=180°,
即∠A+∠B+90°=180°,
所以∠A+∠B=90°.
也就是说,直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,直角三角形ABC也可以写成Rt△ABC.
拓展新知
在三角形ABC中,∠A+∠B=90°,
由三角形内角和定理,得,
∠A+∠B+∠C=180°,
即90°+∠C=180°,
所以∠C=90°.
也就是说,有两个角互余的三角形是直角三角形.
拓展新知
A
B
C
A
D
B
C
【例1】如图,在△ABC中,∠BAC=40°,∠B=
75°,AD是△ABC的角平分线.求∠ADB的度数.
分析:要想求出∠ADB的度数,根据三角形内角和定理,只要求出∠DAB的度数即可.由于∠BAC=40°,AD是△ABC的角平分线,所以很容易得出∠DAB=20°.
例题解析
A
D
B
C
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB=
∠BAC=20°,
∵∠B=75°,
∴∠ADB=180°-∠DAB-∠B
=180°-20°-75°
=85°.
例题解析
A
D
B
C
E
北
北
【例2】如图,是A,B,C三岛的平面图,C岛在A岛
的北偏东50°方向,B岛在A岛的北偏东80°方向,
C岛在B岛的北偏西40°方向,从B岛看A,C两岛的
视角∠ABC是多少度?从C岛看A,B两岛的视角
∠ACB是多少度?
分析:怎样求出∠ACB的度数?根据三角形内角和定理,只需求出∠CAB和∠ABC的度数即可.
例题解析
解:∠CAB=∠BAD-∠CAD=80°-50°=30°.
∵AD∥BE,
∴∠BAD+∠ABE=180°.
∴∠ABE=180°-∠BAD=180°-80°=100°.
∴∠ABC=∠ABE-∠EBC=100°-40°=60°.
∴∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°.
答:从B岛看A,C两岛的视角∠ABC是60°,
从C岛看AB两岛的视角∠ACB=90°.
A
D
B
C
E
北
北
例题解析
D
A
B
C
1.已知三角形三个内角的度数之比为1∶3∶5,
求这三个内角的度数.
2.如图,从A处观测C处时仰角∠CAD=30°,从B
处观测C处时仰角∠CBD=45°.从C处观测A,B
两处时视角∠ACB是多少度?
课堂练习
例题解析
1.解:设三个内角度数分别为:x,3x,5x.
列出方程,得x+3x+5x=180°.
解得:x=20°
答:三个内角度数分别为20°,60°,100°
过点C作CF∥AD,
∴∠1=∠DAC=50°,
∵CF∥AD,AD∥BE,
∴CF∥BE.
∴∠2=∠CBE=40°
∴∠ACB=∠1+∠2=50°+40°=90°.
2.你能想出一个更简捷的方法来求∠ACB的度数吗?
1
2
F
A
D
B
C
E
北
北
例题解析
三角形的内角和等于180°.
证法
应用
转化为一个平角或同旁内角互补
求角度
作平行线
转化思想
辅助线
通过本课时的学习,需要我们掌握:
性质:直角三角形的两个锐角互余.
判定:有两个角互余的三角形是直角三角形.
课堂小结
再见
