人教版八年级上册数学11.2.2《三角形的外角》 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.2.2《三角形的外角》 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 317.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 09:21:27 | ||
图片预览




文档简介
(共16张PPT)
第十一章
三角形
11.2
与三角形有关的角
11.2.2
三角形的外角
学习目标
1.理解三角形外角的概念.
2.通过探索三角形的外角的性质及其应用,培
养主动探索、勇于发现及合作交流的习惯.
A
B
C
D
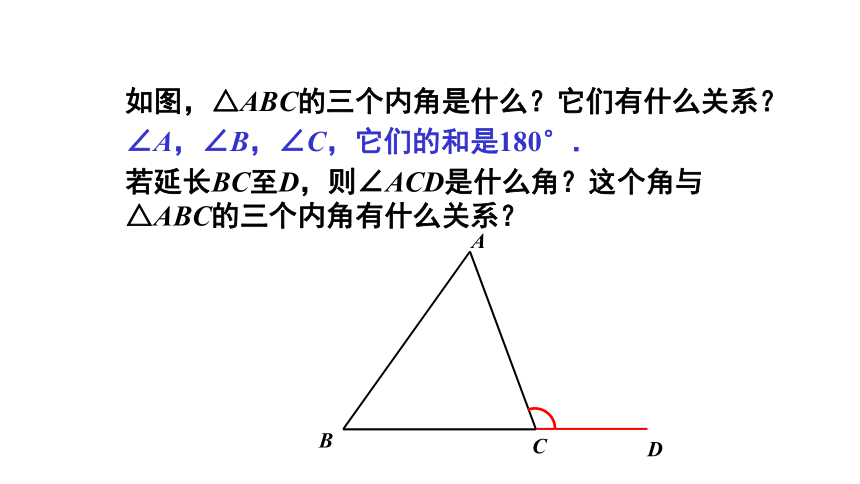
如图,△ABC的三个内角是什么?它们有什么关系?
∠A,∠B,∠C,它们的和是180°.
若延长BC至D,则∠ACD是什么角?这个角与
△ABC的三个内角有什么关系?
情景导入
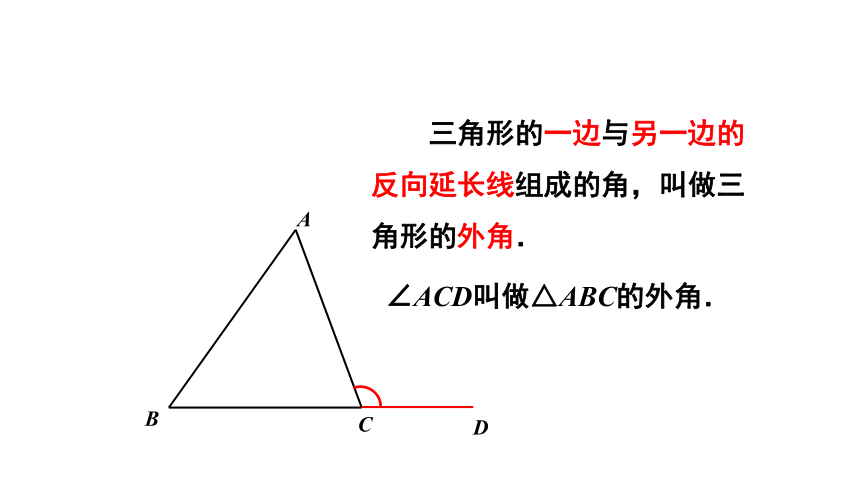
三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
∠ACD叫做△ABC的外角.
探究新知
A
B
C
D
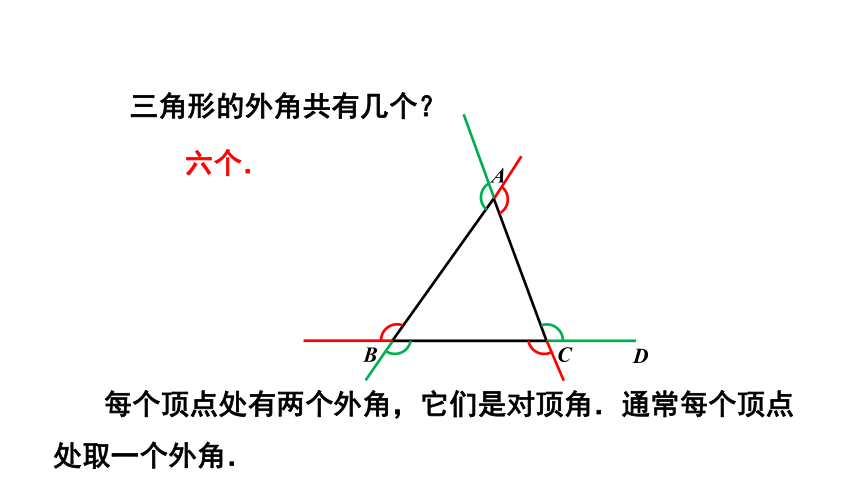
三角形的外角共有几个?
每个顶点处有两个外角,它们是对顶角.通常每个顶点
处取一个外角.
六个.
探究新知
A
B
C
D
三角形的外角∠ACD与相邻的内角∠ACB是邻补角,它与另外两个角有怎样的数量关系呢?
延长BC到D,过C作CE∥BA
.
∵CE∥AB,
∴∠A=∠1,∠B=∠2.
又∠ACD=∠1+∠2,
∴∠ACD=∠A+∠B.
三角形的一个外角等于与它不相邻的两个内角之和.
探究新知
A
B
C
E
1
2
D
小结归纳:
三角形的外角与内角的关系:
(1)三角形的一个外角与它相邻的内角互补;
(2)三角形的一个外角等于与它不相邻的两个内
角的和;
三角形的外角
【例】如图,∠BAE,∠CBF,∠ACD是三角形ABC
的三个外角,它们的和是多少?
例题解析
A
B
C
D
E
F
解法1:由三角形的一个外角等于与它不相邻
的两个内角的和,得
∠BAE=∠2+∠3,
∠CBF=∠1+∠3,
∠ACD=∠1+∠2.
∴∠BAE+∠CBF+∠ACD
=2(∠1+∠2+∠3).
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
A
B
C
例题解析
D
E
F
1
2
3
解法2:
由∠BAE
+∠1
=∠CBF
+∠2
=∠ACD+∠3=180°,得
∠BAE
+∠CBF
+∠ACD
=3×180°-(∠1+∠2+∠3)
=540°-180°
=360°.
例题解析
A
B
C
D
E
F
1
2
3
解法3:
过A作AG平行于BC,
∴∠CBF=∠BAG,
∠ACD=∠EAG
(两直线平行,同位角相等).
∴∠BAE+∠CBF+∠ACD
=∠BAE+∠BAG+∠EAG=360°.
三角形外角的和等于360°.
例题解析
A
B
C
D
E
F
G
(1)三角形的外角和是指三角形所有外角的和.(
)
(2)三角形的外角和等于它内角和的2倍.(
)
(3)三角形的一个外角等于两个内角的和.(
)
(4)三角形的一个外角等于与它不相邻的两个内角的
和.(
)
(5)三角形的一个外角大于任何一个内角.(
)
(6)三角形的一个内角小于任何一个与它不相邻的外
角.(
)
×
√
√
√
×
×
课堂练习
课堂练习
2.如果三角形的一个外角与它不相邻的
两个内角的和为180°,那么与这个外角相邻的
内角的度数为(
).
A.30°
B.60°
C.90°
D.120°
C
1.三角形外角的概念
三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
2.三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
3.三角形的外角和是360°.
课堂小结
再见
第十一章
三角形
11.2
与三角形有关的角
11.2.2
三角形的外角
学习目标
1.理解三角形外角的概念.
2.通过探索三角形的外角的性质及其应用,培
养主动探索、勇于发现及合作交流的习惯.
A
B
C
D
如图,△ABC的三个内角是什么?它们有什么关系?
∠A,∠B,∠C,它们的和是180°.
若延长BC至D,则∠ACD是什么角?这个角与
△ABC的三个内角有什么关系?
情景导入
三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
∠ACD叫做△ABC的外角.
探究新知
A
B
C
D
三角形的外角共有几个?
每个顶点处有两个外角,它们是对顶角.通常每个顶点
处取一个外角.
六个.
探究新知
A
B
C
D
三角形的外角∠ACD与相邻的内角∠ACB是邻补角,它与另外两个角有怎样的数量关系呢?
延长BC到D,过C作CE∥BA
.
∵CE∥AB,
∴∠A=∠1,∠B=∠2.
又∠ACD=∠1+∠2,
∴∠ACD=∠A+∠B.
三角形的一个外角等于与它不相邻的两个内角之和.
探究新知
A
B
C
E
1
2
D
小结归纳:
三角形的外角与内角的关系:
(1)三角形的一个外角与它相邻的内角互补;
(2)三角形的一个外角等于与它不相邻的两个内
角的和;
三角形的外角
【例】如图,∠BAE,∠CBF,∠ACD是三角形ABC
的三个外角,它们的和是多少?
例题解析
A
B
C
D
E
F
解法1:由三角形的一个外角等于与它不相邻
的两个内角的和,得
∠BAE=∠2+∠3,
∠CBF=∠1+∠3,
∠ACD=∠1+∠2.
∴∠BAE+∠CBF+∠ACD
=2(∠1+∠2+∠3).
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
A
B
C
例题解析
D
E
F
1
2
3
解法2:
由∠BAE
+∠1
=∠CBF
+∠2
=∠ACD+∠3=180°,得
∠BAE
+∠CBF
+∠ACD
=3×180°-(∠1+∠2+∠3)
=540°-180°
=360°.
例题解析
A
B
C
D
E
F
1
2
3
解法3:
过A作AG平行于BC,
∴∠CBF=∠BAG,
∠ACD=∠EAG
(两直线平行,同位角相等).
∴∠BAE+∠CBF+∠ACD
=∠BAE+∠BAG+∠EAG=360°.
三角形外角的和等于360°.
例题解析
A
B
C
D
E
F
G
(1)三角形的外角和是指三角形所有外角的和.(
)
(2)三角形的外角和等于它内角和的2倍.(
)
(3)三角形的一个外角等于两个内角的和.(
)
(4)三角形的一个外角等于与它不相邻的两个内角的
和.(
)
(5)三角形的一个外角大于任何一个内角.(
)
(6)三角形的一个内角小于任何一个与它不相邻的外
角.(
)
×
√
√
√
×
×
课堂练习
课堂练习
2.如果三角形的一个外角与它不相邻的
两个内角的和为180°,那么与这个外角相邻的
内角的度数为(
).
A.30°
B.60°
C.90°
D.120°
C
1.三角形外角的概念
三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
2.三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
3.三角形的外角和是360°.
课堂小结
再见
