人教版八年级上册数学11.3.2《多边形的内角和》 课件(共23张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.3.2《多边形的内角和》 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 764.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
第十一章
三角形
11.3
多边形及其内角和
11.3.2
多边形的内角和
学习目标
1.掌握多边形的内角和公式及外角和.
2.运用多边形的内角和公式及外角和解决问题.
情境导入
在一次数学基础知识抢答赛上,王老师出了这么一个问题:某个多边形所有的角加起来等于它的外角和,那么该多边形是几边形?
小敏同学仅用几秒钟就解决了问题,你能吗?
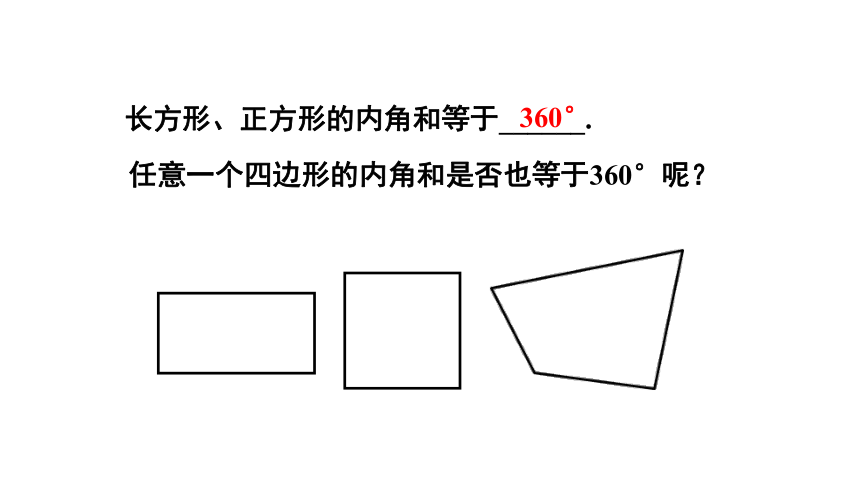
长方形、正方形的内角和等于______.
360°
任意一个四边形的内角和是否也等于360°呢?
探究新知
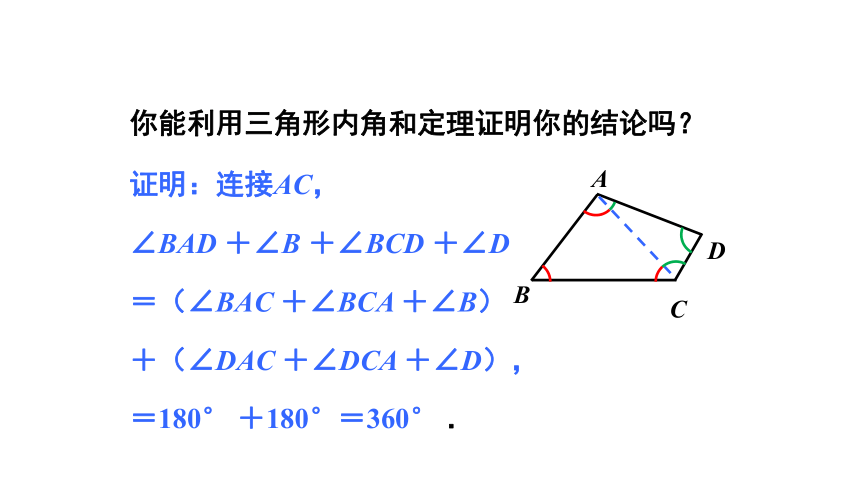
你能利用三角形内角和定理证明你的结论吗?
证明:连接AC,
∠BAD
+∠B
+∠BCD
+∠D
=(∠BAC
+∠BCA
+∠B)
+(∠DAC
+∠DCA
+∠D),
=180°
+180°=360°
.
A
B
C
D
探究新知
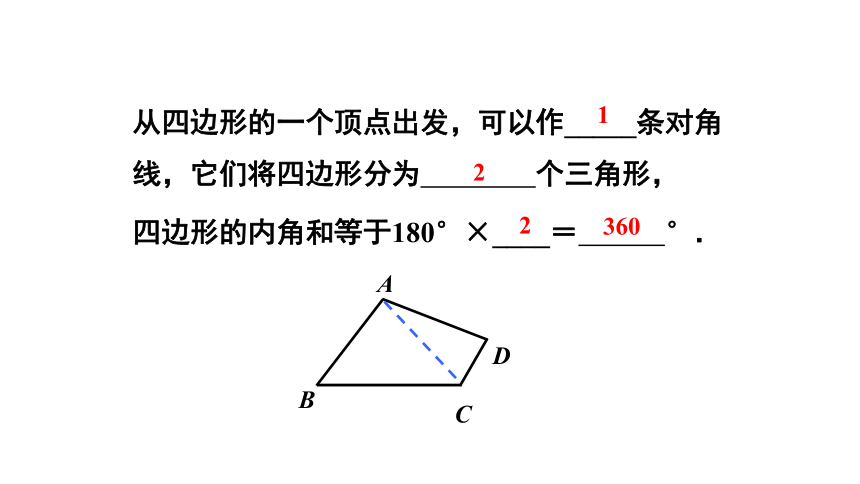
从四边形的一个顶点出发,可以作_____条对角线,它们将四边形分为 个三角形,
四边形的内角和等于180°×____= °.
1
2
2
360
探究新知
A
B
C
D
A
B
C
D
E
如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于180°× =
°.
2
3
3
540
探究新知
A
B
D
E
F
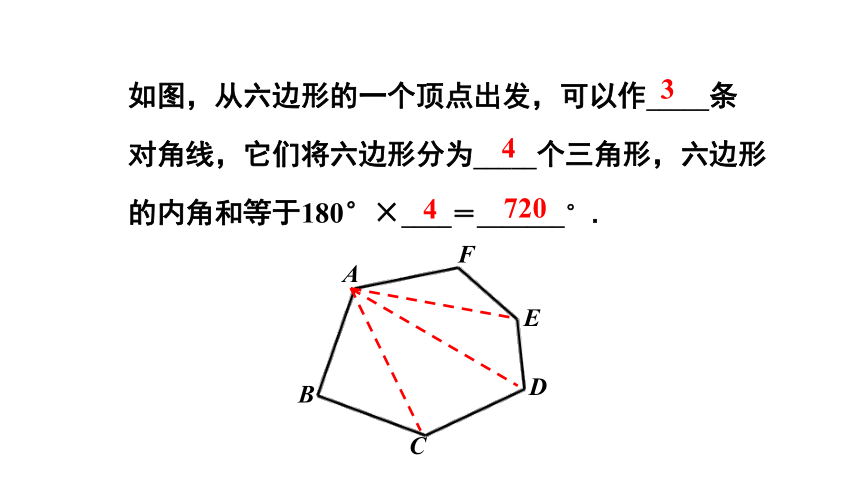
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形
的内角和等于180°×____=_______°.
3
4
4
720
C
探究新知
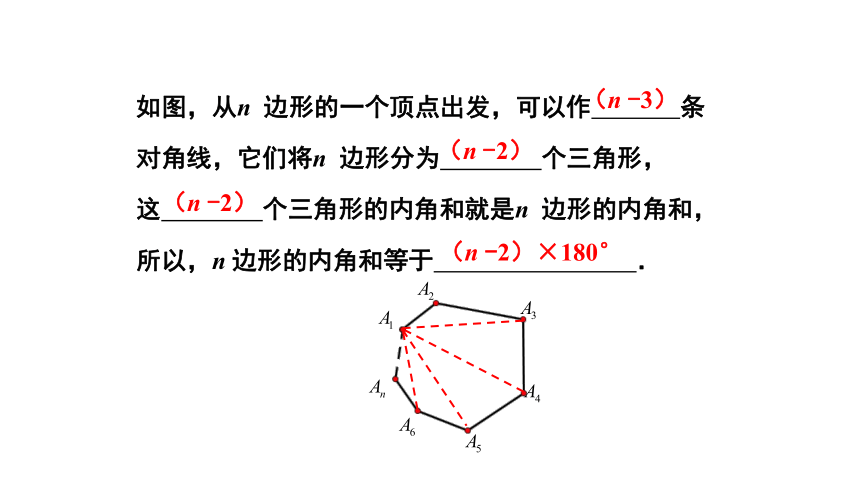
如图,从n
边形的一个顶点出发,可以作
条
对角线,它们将n
边形分为
个三角形,
这
个三角形的内角和就是n
边形的内角和,
所以,n
边形的内角和等于
.
(n
-3)
(n
-2)
(n
-2)×180°
(n
-2)
探究新知
n
边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
···
···
0
3
-3
=
4
-3
=
5
-3
=
6
-3
=
n
-3
1
2
3
3
-2
=
1
4
-2
=
2
5
-2
=
3
6
-2
=
4
n
-2
(
n
-2
)·180?
180?
360?
540?
720?
···
···
···
探究新知
A
B
C
D
E
方法1:如图,
在五边形ABCDE内任取一
点O,连结OA,OB,OC,
OD,OE,则得五个三角形.
∴五边形的内角和为
5×180°-360°=(5-2)×180°=540°.
把一个多边形分成几个三角形,还有其他分法吗?
由新的分法,能得出多边形内角和公式吗?
探究新知
方法2:如图,
在边AB上取一点O,连OE,
OD,OC,则可得(5-1)
个三角形.
∴五边形的内角和为
(5-1)×180°-180°=(5-2)×180°.
A
B
C
D
E
如果把五边形换成n边形,用同样的方法可以得到
n边形内角和为(n-2)×180°.
多边形的内角和
解:如图,四边形ABCD
中,∠A
+∠C
=
180°.
∵∠A
+∠B
+∠C
+∠D
=(4-2)×180°
=360°,
∴∠B
+
∠D
=360°-(∠A
+∠C)=360°-
180°=180°.
【例1】如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
例题解析
【例2】在六边形的每一个顶点处各取一个外
角,这些外角的和叫做六边形的外角和.六边
形的外角和等于多少呢?
如图,已知∠1,∠2,
∠3,∠4,∠5,∠6
分别为六边形ABCDEF
的外角,
求∠1
+∠2
+∠3
+∠4
+∠5
+∠6的值.
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
解:∵∠1
+∠BAF=180°,
∠2
+∠ABC=180°,
∠3
+∠BCD=180°,
∠4
+∠CDE=180°,
∠5
+∠DEF=180°,
∠6
+∠EFA=180°,
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
∴∠1
+∠BAF
+∠2
+∠ABC
+
∠3
+
∠BCD
+∠4
+∠CDE
+∠5
+∠DEF
+∠6
+∠EFA
=6×180°.
又∠BAF
+∠ABC
+∠BCD
+∠CDE
+∠DEF
+∠EFA
=(6-2)×180°,
∴∠1
+∠2
+∠3
+∠4
+∠5
+∠6
=6×180°-(6
-2)×180°=360°
这就是说,六边形的外角和为360°.
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
如果把六边形换成n边形可以得到同样的结果:
因为n边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,
所以n边形内角和加外角和等于n·180°,
所以n边形的外角和等于n·180°-(n-2)·180°=360°.多边形的外角和等于360°.
探究新知
如图,从多边形的一个顶点A
出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发的方向.
A
我们也可以这样理解多边形外角和等于360°.
探究新知
在行程中转过的各个角的和,就是多边形的外角和.由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
A
探究新知
1.一个多边形的内角和是720°,这个多边形的边数是(
)
A.4
B.5
C.6
D.7
2.若一个多边形的边数为8条,则这个多边形的内角和是(
)
A.900°
B.540°
C.1
080°
D.360°
3.若一个多边形增加一条边,那么它的内角和(
)
A.增加180°
B.增加360°C.减少360°
D.不变.
4.多边形每一个内角都等于150°,则该多边形的边数是(
)
A.10
B.11
C.12
D.13
C
A
C
C
课堂练习
(1)多边形内角和公式
(2)多边形外角和等于360°.
(n-2)×180°.
课堂小结
再见
第十一章
三角形
11.3
多边形及其内角和
11.3.2
多边形的内角和
学习目标
1.掌握多边形的内角和公式及外角和.
2.运用多边形的内角和公式及外角和解决问题.
情境导入
在一次数学基础知识抢答赛上,王老师出了这么一个问题:某个多边形所有的角加起来等于它的外角和,那么该多边形是几边形?
小敏同学仅用几秒钟就解决了问题,你能吗?
长方形、正方形的内角和等于______.
360°
任意一个四边形的内角和是否也等于360°呢?
探究新知
你能利用三角形内角和定理证明你的结论吗?
证明:连接AC,
∠BAD
+∠B
+∠BCD
+∠D
=(∠BAC
+∠BCA
+∠B)
+(∠DAC
+∠DCA
+∠D),
=180°
+180°=360°
.
A
B
C
D
探究新知
从四边形的一个顶点出发,可以作_____条对角线,它们将四边形分为 个三角形,
四边形的内角和等于180°×____= °.
1
2
2
360
探究新知
A
B
C
D
A
B
C
D
E
如图,从五边形的一个顶点出发,可以作 条对角线,它们将五边形分为____个三角形,五边形的内角和等于180°× =
°.
2
3
3
540
探究新知
A
B
D
E
F
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形
的内角和等于180°×____=_______°.
3
4
4
720
C
探究新知
如图,从n
边形的一个顶点出发,可以作
条
对角线,它们将n
边形分为
个三角形,
这
个三角形的内角和就是n
边形的内角和,
所以,n
边形的内角和等于
.
(n
-3)
(n
-2)
(n
-2)×180°
(n
-2)
探究新知
n
边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一个顶点引出的对角线条数
图形
边数
···
···
0
3
-3
=
4
-3
=
5
-3
=
6
-3
=
n
-3
1
2
3
3
-2
=
1
4
-2
=
2
5
-2
=
3
6
-2
=
4
n
-2
(
n
-2
)·180?
180?
360?
540?
720?
···
···
···
探究新知
A
B
C
D
E
方法1:如图,
在五边形ABCDE内任取一
点O,连结OA,OB,OC,
OD,OE,则得五个三角形.
∴五边形的内角和为
5×180°-360°=(5-2)×180°=540°.
把一个多边形分成几个三角形,还有其他分法吗?
由新的分法,能得出多边形内角和公式吗?
探究新知
方法2:如图,
在边AB上取一点O,连OE,
OD,OC,则可得(5-1)
个三角形.
∴五边形的内角和为
(5-1)×180°-180°=(5-2)×180°.
A
B
C
D
E
如果把五边形换成n边形,用同样的方法可以得到
n边形内角和为(n-2)×180°.
多边形的内角和
解:如图,四边形ABCD
中,∠A
+∠C
=
180°.
∵∠A
+∠B
+∠C
+∠D
=(4-2)×180°
=360°,
∴∠B
+
∠D
=360°-(∠A
+∠C)=360°-
180°=180°.
【例1】如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
例题解析
【例2】在六边形的每一个顶点处各取一个外
角,这些外角的和叫做六边形的外角和.六边
形的外角和等于多少呢?
如图,已知∠1,∠2,
∠3,∠4,∠5,∠6
分别为六边形ABCDEF
的外角,
求∠1
+∠2
+∠3
+∠4
+∠5
+∠6的值.
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
解:∵∠1
+∠BAF=180°,
∠2
+∠ABC=180°,
∠3
+∠BCD=180°,
∠4
+∠CDE=180°,
∠5
+∠DEF=180°,
∠6
+∠EFA=180°,
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
∴∠1
+∠BAF
+∠2
+∠ABC
+
∠3
+
∠BCD
+∠4
+∠CDE
+∠5
+∠DEF
+∠6
+∠EFA
=6×180°.
又∠BAF
+∠ABC
+∠BCD
+∠CDE
+∠DEF
+∠EFA
=(6-2)×180°,
∴∠1
+∠2
+∠3
+∠4
+∠5
+∠6
=6×180°-(6
-2)×180°=360°
这就是说,六边形的外角和为360°.
A
B
D
E
F
1
2
3
4
5
6
C
例题解析
如果把六边形换成n边形可以得到同样的结果:
因为n边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,
所以n边形内角和加外角和等于n·180°,
所以n边形的外角和等于n·180°-(n-2)·180°=360°.多边形的外角和等于360°.
探究新知
如图,从多边形的一个顶点A
出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发的方向.
A
我们也可以这样理解多边形外角和等于360°.
探究新知
在行程中转过的各个角的和,就是多边形的外角和.由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
A
探究新知
1.一个多边形的内角和是720°,这个多边形的边数是(
)
A.4
B.5
C.6
D.7
2.若一个多边形的边数为8条,则这个多边形的内角和是(
)
A.900°
B.540°
C.1
080°
D.360°
3.若一个多边形增加一条边,那么它的内角和(
)
A.增加180°
B.增加360°C.减少360°
D.不变.
4.多边形每一个内角都等于150°,则该多边形的边数是(
)
A.10
B.11
C.12
D.13
C
A
C
C
课堂练习
(1)多边形内角和公式
(2)多边形外角和等于360°.
(n-2)×180°.
课堂小结
再见
