人教版八年级数学上册暑期课程跟踪——11.3 多边形及其内角和基础练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册暑期课程跟踪——11.3 多边形及其内角和基础练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 173.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 23:02:41 | ||
图片预览

文档简介
11.3
多边形及其内角和基础练习
一、选择题
1.用边长相等的下列两种正多边形,不能进行平面镶嵌的是
A.等边三角形和正六边形
B.正方形和正八边形
C.正五边形和正十边形
D.正六边形和正十二边形
2.
如图,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360°
B.540°
C.720°
D.630°
3.
八边形的内角和等于( )
A.360°
B.1080°
C.1440°
D.2160°
4.下列多边形中,内角和与外角和相等的是( )
A.四边形
B.
五边形
C.
六边形
D.
八边形
5.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于
A.90°
B.180°
C.210°
D.270°
6.
一个正多边形的每个外角不可能等于( )
A.30°
B.50°
C.40°
D.60°
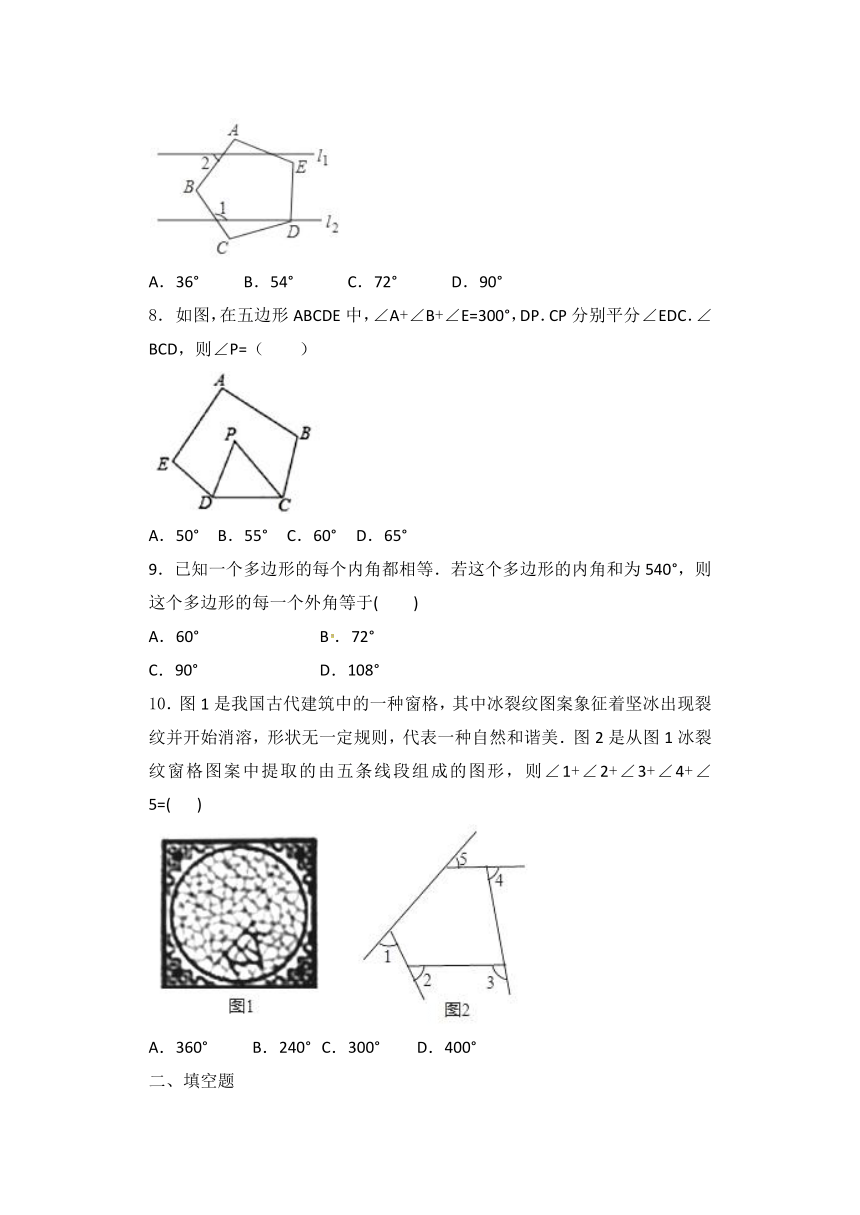
7.如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2=(
)
A.36°
B.54°
C.72°
D.90°
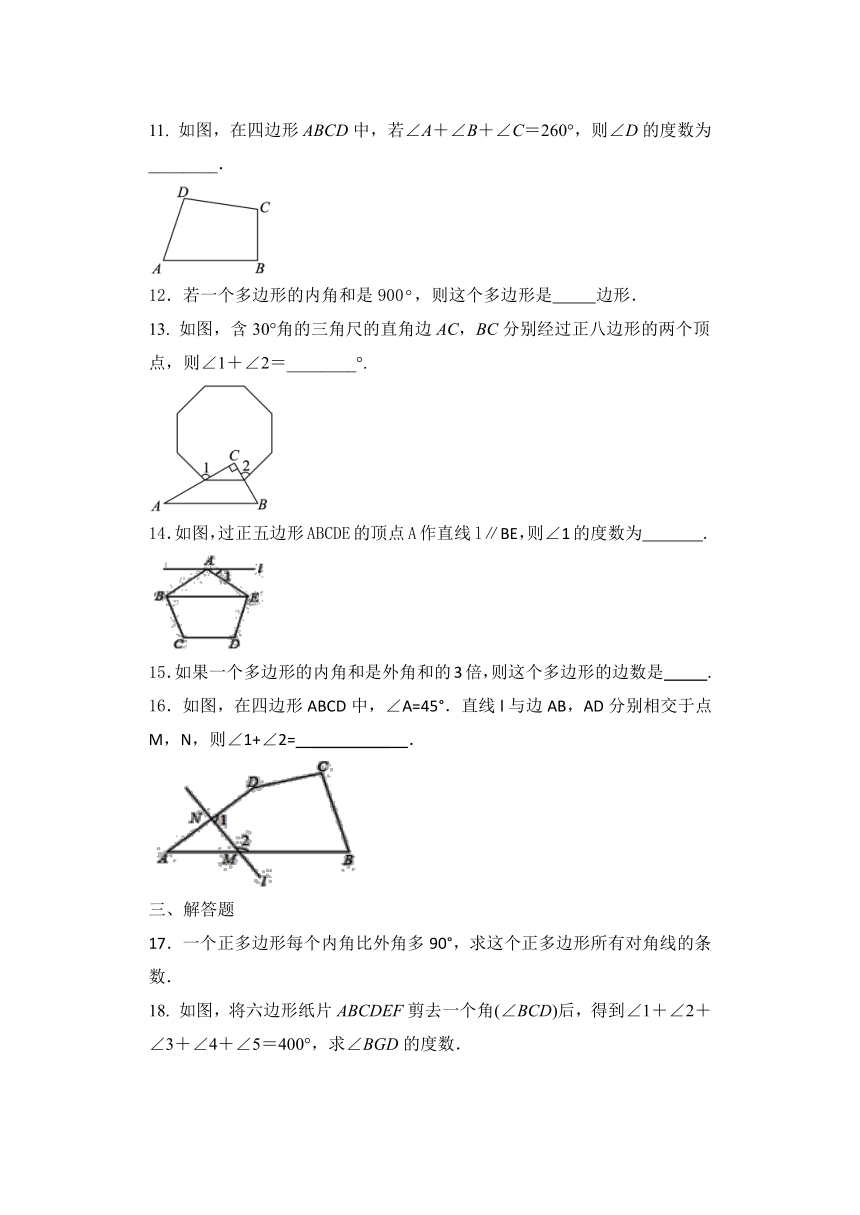
8.
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP.CP分别平分∠EDC.∠BCD,则∠P=( )
A.50°
B.55°
C.60°
D.65°
9.已知一个多边形的每个内角都相等.若这个多边形的内角和为540°,则这个多边形的每一个外角等于( )
A.60°
B.72°
C.90°
D.108°
10.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=(
)
A.360°
B.240°
C.300°
D.400°
二、填空题
11.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为________.
12.若一个多边形的内角和是900?,则这个多边形是
边形.
13.
如图,含30°角的三角尺的直角边AC,BC分别经过正八边形的两个顶点,则∠1+∠2=________°.
14.如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为
.
15.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是
.
16.如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= _________ .
三、解答题
17.一个正多边形每个内角比外角多90°,求这个正多边形所有对角线的条数.
18.
如图,将六边形纸片ABCDEF剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=400°,求∠BGD的度数.
19.(1)如图①,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
(2)如图②,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=________°;
(3)根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是______________.
20.若多边形的所有内角与它的一个外角的和为600°,求边数和内角和.
答案
1.
D
2.
D
3.
B
4.
A
5.
B
6.
B
7.
C
8.
C
9.
B
10.
A
11.
100°
12.
七
13.
180
14.
36°
15.
8
16.
2250
17.
解:设此正多边形为正n边形.
由题意得:=90,
n=8,
∴此正多边形所有的对角线条数为:=20.
答:这个正多边形的所有对角线有20条.
18.
解:∵六边形ABCDEF的内角和为180°×(6-2)=720°,
且∠1+∠2+∠3+∠4+∠5=400°,
∴∠GBC+∠C+∠CDG=720°-400°=320°.
∴∠BGD=360°-(∠GBC+∠C+∠CDG)=40°.
19.
解:(1)∵四边形的内角和为360°,直角三角形中两个锐角的和为90°,
∴∠1+∠2=360°-(∠C+∠B)=360°-90°=270°.
故选C.
(2)在△ABC中,∠A=40°,
∠C+∠B=180°-40°=140°
∴∠1+∠2=360°-(∠C+∠B)=220°,
故答案是:220.
(3)
根据(1)(2)的结果可得:∠1+∠2=180°+∠A
故答案是:∠1+∠2=180°+∠A
20.
五边形
540°
多边形及其内角和基础练习
一、选择题
1.用边长相等的下列两种正多边形,不能进行平面镶嵌的是
A.等边三角形和正六边形
B.正方形和正八边形
C.正五边形和正十边形
D.正六边形和正十二边形
2.
如图,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N不可能是( )
A.360°
B.540°
C.720°
D.630°
3.
八边形的内角和等于( )
A.360°
B.1080°
C.1440°
D.2160°
4.下列多边形中,内角和与外角和相等的是( )
A.四边形
B.
五边形
C.
六边形
D.
八边形
5.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于
A.90°
B.180°
C.210°
D.270°
6.
一个正多边形的每个外角不可能等于( )
A.30°
B.50°
C.40°
D.60°
7.如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2=(
)
A.36°
B.54°
C.72°
D.90°
8.
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP.CP分别平分∠EDC.∠BCD,则∠P=( )
A.50°
B.55°
C.60°
D.65°
9.已知一个多边形的每个内角都相等.若这个多边形的内角和为540°,则这个多边形的每一个外角等于( )
A.60°
B.72°
C.90°
D.108°
10.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=(
)
A.360°
B.240°
C.300°
D.400°
二、填空题
11.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为________.
12.若一个多边形的内角和是900?,则这个多边形是
边形.
13.
如图,含30°角的三角尺的直角边AC,BC分别经过正八边形的两个顶点,则∠1+∠2=________°.
14.如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为
.
15.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是
.
16.如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= _________ .
三、解答题
17.一个正多边形每个内角比外角多90°,求这个正多边形所有对角线的条数.
18.
如图,将六边形纸片ABCDEF剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=400°,求∠BGD的度数.
19.(1)如图①,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
(2)如图②,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=________°;
(3)根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是______________.
20.若多边形的所有内角与它的一个外角的和为600°,求边数和内角和.
答案
1.
D
2.
D
3.
B
4.
A
5.
B
6.
B
7.
C
8.
C
9.
B
10.
A
11.
100°
12.
七
13.
180
14.
36°
15.
8
16.
2250
17.
解:设此正多边形为正n边形.
由题意得:=90,
n=8,
∴此正多边形所有的对角线条数为:=20.
答:这个正多边形的所有对角线有20条.
18.
解:∵六边形ABCDEF的内角和为180°×(6-2)=720°,
且∠1+∠2+∠3+∠4+∠5=400°,
∴∠GBC+∠C+∠CDG=720°-400°=320°.
∴∠BGD=360°-(∠GBC+∠C+∠CDG)=40°.
19.
解:(1)∵四边形的内角和为360°,直角三角形中两个锐角的和为90°,
∴∠1+∠2=360°-(∠C+∠B)=360°-90°=270°.
故选C.
(2)在△ABC中,∠A=40°,
∠C+∠B=180°-40°=140°
∴∠1+∠2=360°-(∠C+∠B)=220°,
故答案是:220.
(3)
根据(1)(2)的结果可得:∠1+∠2=180°+∠A
故答案是:∠1+∠2=180°+∠A
20.
五边形
540°
