1.1 全等图形同步训练题（含解析）

中小学教育资源及组卷应用平台
初中数学苏科版八年级上册1.1
全等图形
同步训练
一、单选题
1.下列说法中正确的是（??
）
A.?面积相等的两个图形是全等形?????????????????????????????B.?周长相等的两个图形是全等形
C.?所有正方形都是全等形???????????????????????????????????????D.?能够完全重合的两个图形是全等形
2.下列说法中，正确的有（???
）
①正方形都是全等形；②等边三角形都是全等形；③形状相同的图形是全等形；④能够完全重合的图形是全等形．
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.下列命题①两个图形全等，它们的形状相同；②两个图形全等，它们的大小相同；③面积相等的两个图形全等；④周长相等的两个图形全等．其中正确的个数为（??
）
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列说法错误的是（　　）
A.?两个面积相等的圆一定全等?????????????????????B.?全等三角形是指形状、大小都相同的三角形
C.?底边相等的两个等腰三角形全等??????????????D.?斜边上中线和一条直角边对应相等的两直角三角形全等
5.下列四个选项中的图形与下面的图形全等的是（?
）
A.????????????????????B.????????????????????C.????????????????????D.?
6.在如图所示的图形中，全等图形有(??
)
A.?1对???????????????????????????????????????B.?2对???????????????????????????????????????C.?3对???????????????????????????????????????D.?4对
7.如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（??
）
A.?90°?????????????????????????????????????B.?135°?????????????????????????????????????C.?150°?????????????????????????????????????D.?180°
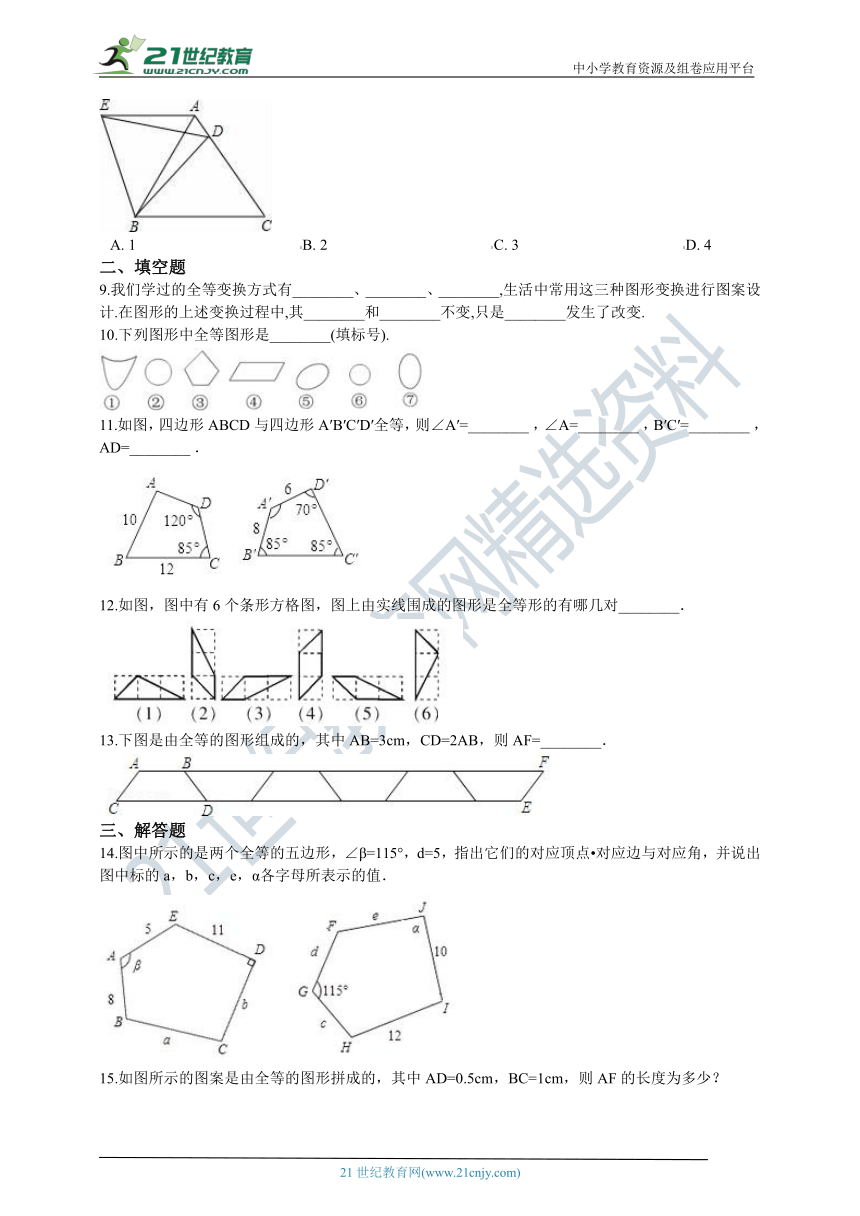
8.在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC＝5，BD＝4，有下列结论：①AE∥BC；②∠ADE＝∠BDC；③△BDE是等边三角形；④△ADE的周长是9．其中，正确结论的个数是（??
）
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
9.我们学过的全等变换方式有________、________、________,生活中常用这三种图形变换进行图案设计.在图形的上述变换过程中,其________和________不变,只是________发生了改变.
10.下列图形中全等图形是________(填标号).
11.如图，四边形ABCD与四边形A′B′C′D′全等，则∠A′=________?，∠A=________?，B′C′=________?，AD=________?．
12.如图，图中有6个条形方格图，图上由实线围成的图形是全等形的有哪几对________．
13.下图是由全等的图形组成的，其中AB=3cm，CD=2AB，则AF=________．
三、解答题
14.图中所示的是两个全等的五边形，∠β=115°，d=5，指出它们的对应顶点?对应边与对应角，并说出图中标的a，b，c，e，α各字母所表示的值．
15.如图所示的图案是由全等的图形拼成的，其中AD=0.5cm，BC=1cm，则AF的长度为多少？
16.找出七巧板中（如图）全等的图形。
17.如图，请沿图中的虚线，用三种方法将下列图形（3×4网格）划分为两个全等图形．
18.
（1）请你沿着图1中的虚线，用两种方法将图1划分为两个全等的图形；
（2）如图2，是
的正方形网格，其中已有3个小方格涂成了阴影，请你从其余的13个白色的小方格中选出一个也涂成阴影，使整个涂成阴影的图形成为轴对称图形.请用三种方法在图中补全图形，并画出它们各自的对称轴（所画的三个图形不能全等）
答案解析部分
一、单选题
1.【答案】
D
【考点】全等图形
解：因为能够完全重合的两个图形是全等形，所以选D.
【分析】全等形：能够完全重合的两个图形是全等形。
2.【答案】
A
【考点】全等图形
解：①正方形的周长不一定相等，故正方形不是全等形，①错误；
②等边三角形的周长不一定相等，故等边三角形不是全等形，②错误；
③形状相同、大小相等的图形是全等形，③错误；
④能够完全重合的图形是全等形，④正确.
故答案为：A
【分析】①正方形的边长不一定相等，所以正方形不一定是全等形；
②等边三角形的边长不一定相等，所以等边三角形不一定是全等形；
③根据能够完全重合的两个图形是全等形可知形状相同的图形不一定是全等形；
④全等形的定义，能够完全重合的图形是全等形。
3.【答案】
B
【考点】全等图形
解：①两个图形全等，它们的形状相同，正确；
②两个图形全等，它们的大小相同，正确；
③面积相等的两个图形全等，错误；
④周长相等的两个图形全等，错误．
所以只有2个正确，
故答案为：B。
【分析】能够完全重合的两个图形叫做全等形．强调能够完全重合，对选择项进行验证可得答案．
4.【答案】
C
【考点】全等图形
解：A、两个面积相等的圆一定全等，说法正确；
B、全等三角形是指形状、大小都相同的三角形，说法正确；
C、底边相等的两个等腰三角形全等，说法错误；
D、斜边上中线和一条直角边对应相等的两直角三角形全等，说法正确；
故选：C．
【分析】根据圆的面积公式可得两个面积相等的圆半径一定也相等，故A说法正确；根据全等三角形的概念可得B说法正确；底边相等的两个等腰三角形，腰长不一定相等，故C说法错误；斜边上中线相等的直角三角形，斜边也相等，再有一条直角边对应相等，故两个直角三角形全等，因此D说法正确．
5.【答案】
B
【考点】全等图形
解：能够与已知图形重合的只有
．故答案为：B．
【分析】根据能够完全重合的两个图形是全等形即可判断。
6.【答案】
C
【考点】全等图形
解：图中全等图形是：笑脸，箭头，五角星.
故答案为：C
【分析】根据能够完全重合的两个图形是全等形即可判断。
7.【答案】B
【考点】全等图形
解：如图，在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠1=∠4，
∵∠3+∠4=90°，
∴∠1+∠3=90°，
又∵∠2=45°，
∴∠1+∠2+∠3=90°+45°=135°．
故选B．
【分析】标注字母，利用“边角边”判断出△ABC和△DEA全等，根据全等三角形对应角相等可得∠1=∠4，然后求出∠1+∠3=90°，再判断出∠2=45°，然后计算即可得解．
8.【答案】
C
【考点】全等图形，全等三角形的性质，图形的旋转
解：∵△ABC为等边三角形，∴∠ABC=∠C=60°，AC=BC=5.
∵△BCD绕点B逆时针旋转60°，得到△BAE，
∴∠BAE=∠C=60°，AE=CD.
∴∠BAE=∠ABC，
∴AE∥BC，所以①正确；
∵△BCD绕点B逆时针旋转60°，得到△BAE，
∴∠DBE=60°，BD=BE=4.
∴△BDE为等边三角形，所以③正确.
∵∠BDC=∠BAC+∠ABD>60°，∠ADE+∠BDC=180°-∠BDE=120°，
∴∠ADE<∠BDC,∴②一定错误；
∵AE=CD，DE=BD=4，
∴△ADE的周长=AD+AE+DE=AD+CD+DB=AC+BD=5+4=9，所以④正确．
故答案为：C.
【分析】本题的关键点在先证出三角形全等，再利用全等三角形的性质、平行线的性质及判定进行证明。
二、填空题
9.【答案】平移；旋转；轴对称；形状；大小；位置
【考点】全等图形，轴对称图形，图形的旋转，图形的平移
解：我们学过的全等变换方式有平移、旋转、轴对称，生活中常用这三种图形变换进行图案设计.在图形的上述变换过程中,其形状和大小不变，只是位置发生了变化。
故答案为：平移、旋转、轴对称、形状、大小、位置.【分析】学过的全等变换最基本的有平移、旋转、轴对称，再变换的过程中，图形的形状和大小不变，位置要变，即可得出答案。
10.【答案】
⑤和⑦
【考点】全等图形
解：由全等形的概念可知：共有1对图形全等，即⑤和⑦能够重合，故答案为⑤和⑦.
【分析】能够完全重合的两个图形是全等图形，据此逐一判断即可.
11.【答案】120；70；12；6
【考点】全等图形
解：∵四边形ABCD与四边形A′B′C′D′全等，由题意得：∠A′=∠D
=∠120°，∠D′=∠A=70°，B′C′=CB=12，AD
=
D′A′=6
【分析】根据全等形的对应边相等、对应角相等即可求解。
12.【答案】（1）和（6），（2）（3）（5）
【考点】全等图形
解：设每个小方格的边长为1，则：（1）的各边分别是3，
；（2）的各边长分别是：
，1，
，2；（3）的各边长分别是：
，1，
，2；（4）的各边长分别是：2，
，2，
；（5）的各边长分别是：
，1，
，2；（6）的各边分别是3，
；
故（1）（6）是全等形，（2）（3）（5）是全等形．
【分析】根据能够完全重合的图形是全等形可求解。
13.【答案】
27cm
【考点】全等图形
解：因为AB=3cm，所以CD=2AB=6cm，
所以AF=3AB+3CD=3×3+3×6=27（cm）．
故答案为：27cm．
【分析】由全等图形的对应边相等可知，AF=3（AB+CD），再将已知条件代入计算即可求解。
三、解答题
14.【答案】
解：对应顶点：A和G，E和F，D和J，C和I，B和H，
对应边：AB和GH，AE和GF，ED和FJ，CD和JI，BC和HI；
对应角：∠A和∠G，∠B和∠H，∠C和∠I，∠D和∠J，∠E和∠F；
∵两个五边形全等，
∴a=12，c=8，b=10，e=11，α=90°
【考点】全等图形
【解析】【分析】根据能够完全重合的两个图形是全等形可求解。
15.【答案】解：由题可知，图中有8个全等的梯形，所以AF=4AD+4BC=4×0.5+4×1=6cm
【考点】全等图形
【解析】【分析】由图形知，所示的图案是由梯形ABCD和七个与它全等的梯形拼接而成，根据全等则重合的性质有AF=4AD+4BC=4×0.5+4×1=6cm．
16.【答案】解：由图知：△ADE与△DEC，△EHK与△CJF，△ADC与△ABC，四边形AGKE与四边形CFKE，四边形AGKD与四边形CFKD是重合的，即是全等的图形
【考点】全等图形
【解析】【分析】全等的图形包括全等三角形和全等的四边形，三i角形有3对，四边形有2对.
17.【答案】
解：如图
【考点】全等图形
【解析】【分析】利用全等三角形的定义进行分析画出图形即可。
18.【答案】
（1）解：如图：
（2）解：如图：
【考点】全等图形，轴对称图形
【解析】【分析】(1)根据全等图形的概念，可先从面积上考虑将图形分形大小相等的两块，然后从形状上考虑，所分成的两部分必须形状相同即可，注意答案不唯一；
(2)根据轴对称图形的概念，添加部分与原来的能构成轴对称图形即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)