第1章 全等三角形单元测试(基础篇)(含解析)
文档属性
| 名称 | 第1章 全等三角形单元测试(基础篇)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 21:36:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级上册第1章
全等三角形
单元测试(基础篇)
一、单选题
1.下列命题中,真命题是(?
??
).
A.?周长相等的锐角三角形都全等;?????????????????????????B.?周长相等的直角三角形都全等;
C.?周长相等的钝角三角形都全等;?????????????????????????D.?周长相等的等腰直角三角形都全等.
2.在下列四组条件中,能判定△ABC≌△DEF的是(?????
)
A.?AB=DE
,
BC=
EF
,
∠A=∠D??????
??????????????B.?∠A=∠D
,
∠C=∠F
,
AC=
DE
C.?∠A=∠E
,
∠B=∠F
,
∠C=∠D
???????????????????D.?AB=DE
,
BC=
EF
,
△ABC的周长等于△DEF的周长
3.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列各图中,a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是(???
)
A.?甲和乙????????????????????????????????B.?只有乙????????????????????????????????C.?甲和丙????????????????????????????????D.?乙和丙
5.如图,在□ABCD中,延长CD到E
,
使DE=CD
,
连接BE交AD于点F
,
交AC于点G
.
下列结论中:①DE=DF;②AG=GF;③AF=DF;④BG=GC;⑤BF=EF
,
其中正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
6.下面三个命题:
底边和顶角对应相等的两个等腰三角形全等;
两边及其中一边上的中线对应相等的两个三角形全等;
斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为________.
7.如图,已知
,
和
是对应顶点,若
,
,则
________°.
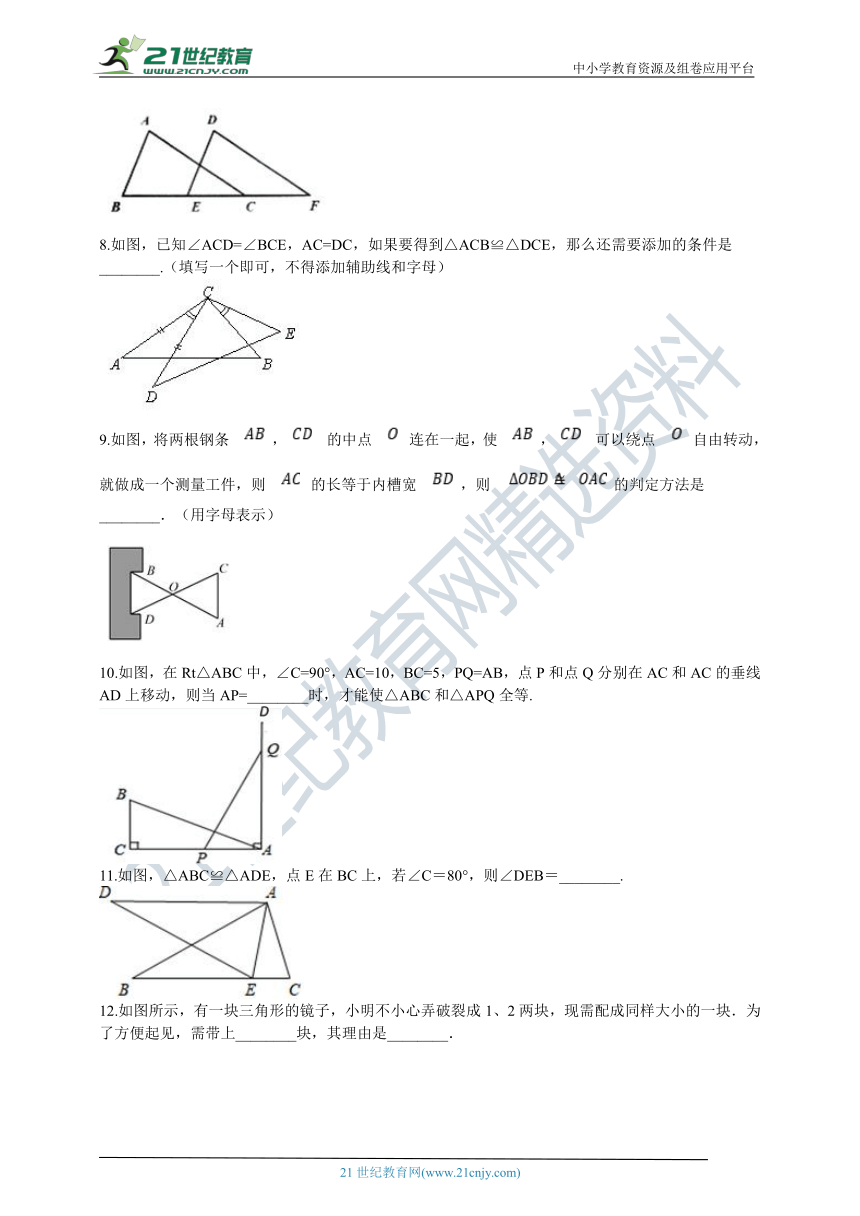
8.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是________.(填写一个即可,不得添加辅助线和字母)
9.如图,将两根钢条
,
的中点
?连在一起,使
,
可以绕点
?自由转动,就做成一个测量工件,则
?的长等于内槽宽
,则?
的判定方法是________.(用字母表示)
10.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,PQ=AB,点P和点Q分别在AC和AC的垂线AD上移动,则当AP=________时,才能使△ABC和△APQ全等.
11.如图,△ABC≌△ADE,点E在BC上,若∠C=80°,则∠DEB=________.
12.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上________块,其理由是________.
13.如图,
,
.
,点
在线段
上以
的速度由点
向点
运动,同时,点
在线段
上由点
向点
运动.它们运动的时间为
.设点
的运动速度为
,若使得
全等,则
的值为________.
三、解答题
14.如图,
,点
在边
上,
与
交于点
,已知
,
,求
的度数.
15.已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.
求证:△ABC≌△DEF.
16.如图,已知在四边形ABCD中,点E在AD上,∠B+∠AEC=180°,∠BAC=∠D,BC=CE.求证:AC=DC.
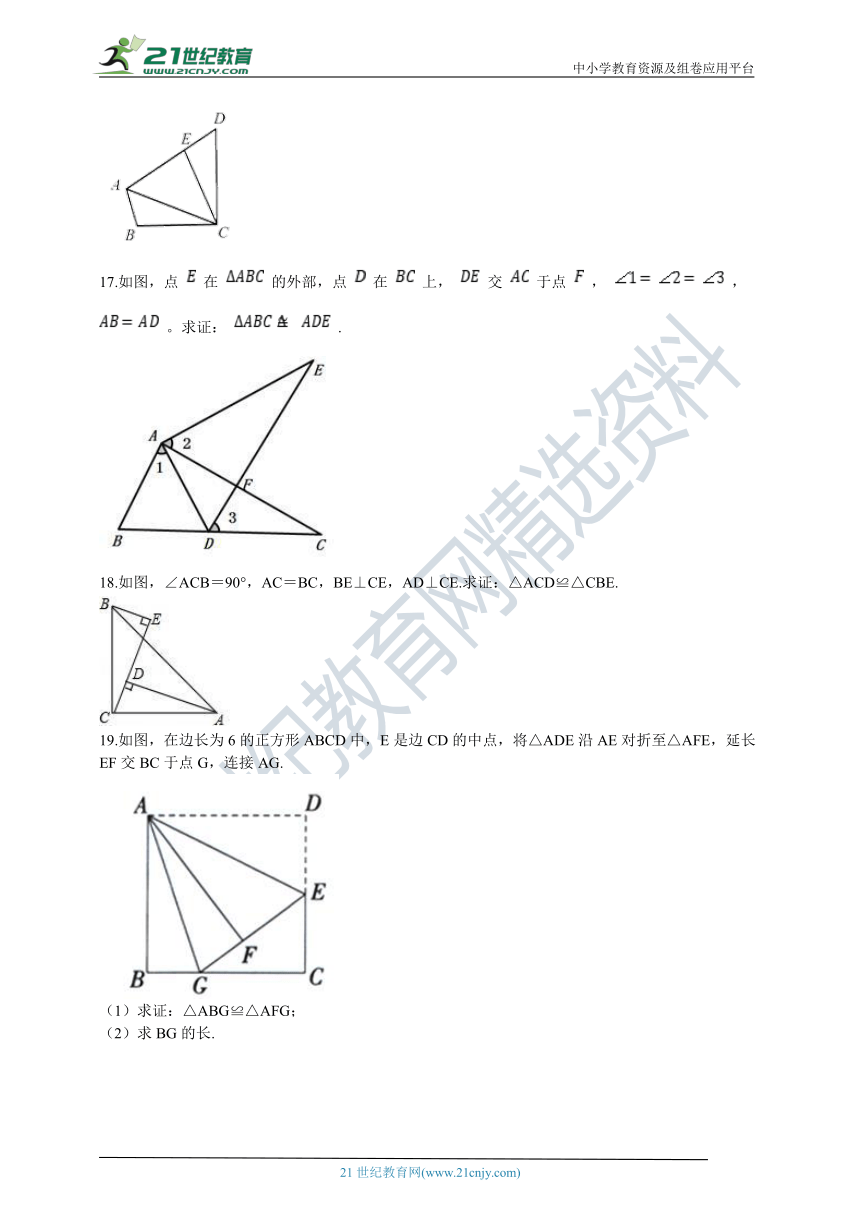
17.如图,点
在
的外部,点
在
上,
交
于点
,
,
。求证:
.
18.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.
19.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
答案解析部分
一、单选题
1.【答案】
D
【考点】三角形全等的判定
【解析】
【分析】全等三角形必须是对应角相等,对应边相等,根据全等三角形的判定方法,逐一检验.
【解答】A、周长相等的锐角三角形的对应角不一定相等,对应边也不一定相等,假命题;
B、周长相等的直角三角形对应锐角不一定相等,对应边也不一定相等,假命题;
C、周长相等的钝角三角形对应钝角不一定相等,对应边也不一定相等,假命题;
D、由于等腰直角三角形三边之比为1:1:,故周长相等时,等腰直角三角形的对应角相等,对应边相等,故全等,真命题.
故选D.
2.【答案】
D
【考点】三角形全等的判定
解:A中不是夹角相等;B中不是夹边相等;C中没有至少一条边;
故答案为:D。
【分析】此题综合考查了三角形全等的判定方法,把常常出错的地方都进行了强化训练,是一道不错的综合性质题目.
3.【答案】
C
【考点】全等三角形的性质
解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;
∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④正确;
条件不足,无法证明∠FAB=∠EAB,故②错误;
综上所述,结论正确的是①③④共3个.
故答案为:C.
【分析】根据全等三角形的对应角相等,对应边相等即可一一判断得出答案.
4.【答案】
D
【考点】三角形全等的判定
解:∵a=a,c=c,边a和边c的夹角相等
∴乙和三角形ABC全等(SAS)
∵50°=50°,72°=72°,且72°所对的a=72°所对的a
∴三角形ABC和丙全等(AAS)
故答案为:D.
【分析】根据三角形全等的判定定理,分别判断得到答案即可。
5.【答案】
B
【考点】全等三角形的性质,三角形全等的判定
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∴∠ABF=∠E,
∵DE=CD,
∴AB=DE,
在△ABF和△DEF中,
∵
,
∴△ABF≌△DEF(AAS),
∴AF=DF,BF=EF;
可得③⑤符合题意,
故答案为:B.
【分析】由AAS证明△ABF≌△DEF,得出对应边相等AF=DF,BF=EF,即可得出结论,对于①②④不一定符合题意.
二、填空题
6.【答案】
【考点】三角形全等的判定
解:
解:
①
底边和顶角对应相等的两个等腰三角形全等;正确;
②
两边及其中一边上的中线对应相等的两个三角形全等;正确;
③
斜边和斜边上的中线对应相等的两个直角三角形全等;错误;
故答案为:
①②
.
【分析】判断三角形全等的条件:三边对应相等的三角形是全等三角形
两边及其夹角对应相等的三角形是全等三角形
两角及其夹边对应相等的三角形是全等三角形
两角及其一角的对边对应相等的三角形是全等三角形
在直角三角形中,斜边和一直角边相等的是全等三角形
?
7.【答案】
35
【考点】全等三角形的性质
解:∵△ABC≌△DEF,A与D是对应顶点,
∴∠F=∠ACB,
又∵∠A=80°,∠B=65°,
∴∠ACB=180°-80°-65°=35°
∴∠F=∠ACB=35°
所以应填35.
【分析】依据全等三角形对应角相等及三角形内角和为180°,可求解∠F的大小.
8.【答案】
∠A=∠D
【考点】三角形全等的判定
解:A=∠D,
理由是:∵∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
∴∠ACB=∠DCE,
在△ACB和△DCE中
,
∴△ACB≌△DCE(ASA),
故答案为:∠A=∠D.
【分析】开放性的命题,答案不唯一,由已知条件可以得出∠ACB=∠DCE,又题干给出了
AC=DC
,根据三角形全等的判定方法再添加
∠A=∠D或∠B=∠E或BC=EC
即可.
9.【答案】
SAS
【考点】三角形全等的判定
解:∵两钢条中点连在一起做成一个测量工件,
∴OA=OB,OD=OC,
∵∠AOC=∠DOB,
∴△OBD≌△OAC.
所以BD的长等于内槽宽AC,
用的是SAS的判定定理.
故答案是:SAS.
【分析】根据用两钢条中点连在一起做成一个测量工件,可求出两边分别对应相等,再加上对顶角相等,可判断出两个三角形全等,且用的是SAS.
10.【答案】
5或10
【考点】三角形全等的判定
解:∵PQ=AB,∴根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,△ABC≌△QPA,即AP=BC=5;
②当P运动到与C点重合时,△QAP≌△BCA,即AP=AC=10.
故答案为:5或10.
【分析】本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5,可据此求出P点的位置;
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
11.【答案】
20°
【考点】全等三角形的性质
解:∵△ABC≌△ADE,
∴∠C=∠AED=80°,AC=AE,
∴∠AEC=∠C=80°,
∴∠DEB=180°?80°?80°=20°,
故答案为:20°.
【分析】根据全等三角形的性质可得∠C=∠AED=80°,AC=AE,利用等边对等角可得∠AEC=∠C=80°,利用平角定义求出∠DEB的度数即可.
12.【答案】
第1;利用SAS得出全等三角形,即可配成与原来同样大小的一块
【考点】三角形全等的判定
解:为了方便起见,需带上第1块,
其理由是:利用SAS得出全等三角形,即可配成与原来同样大小的一块.
故答案为:第1,利用SAS得出全等三角形,即可配成与原来同样大小的一块.
【分析】利用SAS,进而得出全等的三角形,进而求出即可.
13.【答案】
2
【考点】全等三角形的性质
解:
,
,
运动时间相同,
,
的运动速度也相同,
.
故答案为
【分析】根据全等三角形的性质可知PA=BQ,根据路程、速度、时间之间的关系即可判断
三、解答题
14.【答案】
解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABD=∠CBE=132°÷2=66°.
又由△ABC≌△DBE,
∴AB=BD,∠A=∠BDE,
∴∠ADB=∠A=∠BDE=(180°-∠ABD)÷2=57°.
∴∠CDE=180°-∠ADB-∠BDE=66°.
【考点】全等三角形的性质
【解析】【分析】根据全等三角形的性质得到∠ABC=∠DBE,进而得出∠ABD=∠CBE,又由全等可得AB=BD,由等边对等角可得出∠ADB=∠A=∠BDE,最后可得出∠CDE的度数..
15.【答案】
证明:BF=CE,BF+FC=FC+CE,即BC=EF
AC//DF,
在△ABC和△DEF中
△ABC≌△DEF
【考点】三角形全等的判定
【解析】【分析】由题意用角角边可证△ABC≌△DEF.
16.【答案】
证明:∵∠B+∠AEC=180°,∠CED+∠AEC=180°
∴∠B=∠DEC
在△ABC和△DEC中
∴△ABC≌△DEC(AAS)
∴
【考点】余角、补角及其性质,三角形全等的判定
【解析】【分析】根据同角的补角相等,即可得到∠B=∠DEC,根据三角形的任意两个角及其一个角的对边相等,即可得到两个三角形全等,得出答案即可。
17.【答案】
解:∵∠1=∠2,
∴∠BAC=∠DAE.
∵∠1=∠3,
又∵∠ADC=∠1+∠B=∠3+∠ADE,
∴∠B=∠ADE.
在△ABC和△ADE中,
∴
【考点】三角形全等的判定
【解析】【分析】∠1=∠2可以推出∠BAC=∠DAE,根据外角定理可以推出∠B=∠ADE,再由AB=AD,即可证明.
18.【答案】
解:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,
∠ADC=∠E=90°,∠B=∠ACD,AC=BC,
∴△ACD≌△CBE(AAS).
【考点】三角形全等的判定
【解析】【分析】根据同角的余角相等得出
∠B=∠ACD,
从而利用AAS判断出
△ACD≌△CBE
。
19.【答案】
(1)∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB
,
由折叠的性质可知
AD=AF
,
∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF
,
∴∠AFG=∠B
,
又AG=AG
,
∴△ABG≌△AFG;
(2)∵△ABG≌△AFG
,
∴BG=FG
,
设BG=FG=
,则GC=
,
∵E为CD的中点,
∴CF=EF=DE=3,
∴EG=
,
∴
,
解得
,
∴BG=2
【考点】全等三角形的性质,勾股定理,翻折变换(折叠问题)
【解析】【分析】(1)根据正方形的性质以及折叠的性质即可得到证明三角形全等。
(2)根据全等三角形的性质,可以设BG=FG=x,根据勾股定理计算出x的值,得
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级上册第1章
全等三角形
单元测试(基础篇)
一、单选题
1.下列命题中,真命题是(?
??
).
A.?周长相等的锐角三角形都全等;?????????????????????????B.?周长相等的直角三角形都全等;
C.?周长相等的钝角三角形都全等;?????????????????????????D.?周长相等的等腰直角三角形都全等.
2.在下列四组条件中,能判定△ABC≌△DEF的是(?????
)
A.?AB=DE
,
BC=
EF
,
∠A=∠D??????
??????????????B.?∠A=∠D
,
∠C=∠F
,
AC=
DE
C.?∠A=∠E
,
∠B=∠F
,
∠C=∠D
???????????????????D.?AB=DE
,
BC=
EF
,
△ABC的周长等于△DEF的周长
3.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列各图中,a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是(???
)
A.?甲和乙????????????????????????????????B.?只有乙????????????????????????????????C.?甲和丙????????????????????????????????D.?乙和丙
5.如图,在□ABCD中,延长CD到E
,
使DE=CD
,
连接BE交AD于点F
,
交AC于点G
.
下列结论中:①DE=DF;②AG=GF;③AF=DF;④BG=GC;⑤BF=EF
,
其中正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
6.下面三个命题:
底边和顶角对应相等的两个等腰三角形全等;
两边及其中一边上的中线对应相等的两个三角形全等;
斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为________.
7.如图,已知
,
和
是对应顶点,若
,
,则
________°.
8.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是________.(填写一个即可,不得添加辅助线和字母)
9.如图,将两根钢条
,
的中点
?连在一起,使
,
可以绕点
?自由转动,就做成一个测量工件,则
?的长等于内槽宽
,则?
的判定方法是________.(用字母表示)
10.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,PQ=AB,点P和点Q分别在AC和AC的垂线AD上移动,则当AP=________时,才能使△ABC和△APQ全等.
11.如图,△ABC≌△ADE,点E在BC上,若∠C=80°,则∠DEB=________.
12.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上________块,其理由是________.
13.如图,
,
.
,点
在线段
上以
的速度由点
向点
运动,同时,点
在线段
上由点
向点
运动.它们运动的时间为
.设点
的运动速度为
,若使得
全等,则
的值为________.
三、解答题
14.如图,
,点
在边
上,
与
交于点
,已知
,
,求
的度数.
15.已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.
求证:△ABC≌△DEF.
16.如图,已知在四边形ABCD中,点E在AD上,∠B+∠AEC=180°,∠BAC=∠D,BC=CE.求证:AC=DC.
17.如图,点
在
的外部,点
在
上,
交
于点
,
,
。求证:
.
18.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.
19.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
答案解析部分
一、单选题
1.【答案】
D
【考点】三角形全等的判定
【解析】
【分析】全等三角形必须是对应角相等,对应边相等,根据全等三角形的判定方法,逐一检验.
【解答】A、周长相等的锐角三角形的对应角不一定相等,对应边也不一定相等,假命题;
B、周长相等的直角三角形对应锐角不一定相等,对应边也不一定相等,假命题;
C、周长相等的钝角三角形对应钝角不一定相等,对应边也不一定相等,假命题;
D、由于等腰直角三角形三边之比为1:1:,故周长相等时,等腰直角三角形的对应角相等,对应边相等,故全等,真命题.
故选D.
2.【答案】
D
【考点】三角形全等的判定
解:A中不是夹角相等;B中不是夹边相等;C中没有至少一条边;
故答案为:D。
【分析】此题综合考查了三角形全等的判定方法,把常常出错的地方都进行了强化训练,是一道不错的综合性质题目.
3.【答案】
C
【考点】全等三角形的性质
解:∵△ABC≌△AEF,
∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;
∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④正确;
条件不足,无法证明∠FAB=∠EAB,故②错误;
综上所述,结论正确的是①③④共3个.
故答案为:C.
【分析】根据全等三角形的对应角相等,对应边相等即可一一判断得出答案.
4.【答案】
D
【考点】三角形全等的判定
解:∵a=a,c=c,边a和边c的夹角相等
∴乙和三角形ABC全等(SAS)
∵50°=50°,72°=72°,且72°所对的a=72°所对的a
∴三角形ABC和丙全等(AAS)
故答案为:D.
【分析】根据三角形全等的判定定理,分别判断得到答案即可。
5.【答案】
B
【考点】全等三角形的性质,三角形全等的判定
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∴∠ABF=∠E,
∵DE=CD,
∴AB=DE,
在△ABF和△DEF中,
∵
,
∴△ABF≌△DEF(AAS),
∴AF=DF,BF=EF;
可得③⑤符合题意,
故答案为:B.
【分析】由AAS证明△ABF≌△DEF,得出对应边相等AF=DF,BF=EF,即可得出结论,对于①②④不一定符合题意.
二、填空题
6.【答案】
【考点】三角形全等的判定
解:
解:
①
底边和顶角对应相等的两个等腰三角形全等;正确;
②
两边及其中一边上的中线对应相等的两个三角形全等;正确;
③
斜边和斜边上的中线对应相等的两个直角三角形全等;错误;
故答案为:
①②
.
【分析】判断三角形全等的条件:三边对应相等的三角形是全等三角形
两边及其夹角对应相等的三角形是全等三角形
两角及其夹边对应相等的三角形是全等三角形
两角及其一角的对边对应相等的三角形是全等三角形
在直角三角形中,斜边和一直角边相等的是全等三角形
?
7.【答案】
35
【考点】全等三角形的性质
解:∵△ABC≌△DEF,A与D是对应顶点,
∴∠F=∠ACB,
又∵∠A=80°,∠B=65°,
∴∠ACB=180°-80°-65°=35°
∴∠F=∠ACB=35°
所以应填35.
【分析】依据全等三角形对应角相等及三角形内角和为180°,可求解∠F的大小.
8.【答案】
∠A=∠D
【考点】三角形全等的判定
解:A=∠D,
理由是:∵∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
∴∠ACB=∠DCE,
在△ACB和△DCE中
,
∴△ACB≌△DCE(ASA),
故答案为:∠A=∠D.
【分析】开放性的命题,答案不唯一,由已知条件可以得出∠ACB=∠DCE,又题干给出了
AC=DC
,根据三角形全等的判定方法再添加
∠A=∠D或∠B=∠E或BC=EC
即可.
9.【答案】
SAS
【考点】三角形全等的判定
解:∵两钢条中点连在一起做成一个测量工件,
∴OA=OB,OD=OC,
∵∠AOC=∠DOB,
∴△OBD≌△OAC.
所以BD的长等于内槽宽AC,
用的是SAS的判定定理.
故答案是:SAS.
【分析】根据用两钢条中点连在一起做成一个测量工件,可求出两边分别对应相等,再加上对顶角相等,可判断出两个三角形全等,且用的是SAS.
10.【答案】
5或10
【考点】三角形全等的判定
解:∵PQ=AB,∴根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,△ABC≌△QPA,即AP=BC=5;
②当P运动到与C点重合时,△QAP≌△BCA,即AP=AC=10.
故答案为:5或10.
【分析】本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5,可据此求出P点的位置;
②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
11.【答案】
20°
【考点】全等三角形的性质
解:∵△ABC≌△ADE,
∴∠C=∠AED=80°,AC=AE,
∴∠AEC=∠C=80°,
∴∠DEB=180°?80°?80°=20°,
故答案为:20°.
【分析】根据全等三角形的性质可得∠C=∠AED=80°,AC=AE,利用等边对等角可得∠AEC=∠C=80°,利用平角定义求出∠DEB的度数即可.
12.【答案】
第1;利用SAS得出全等三角形,即可配成与原来同样大小的一块
【考点】三角形全等的判定
解:为了方便起见,需带上第1块,
其理由是:利用SAS得出全等三角形,即可配成与原来同样大小的一块.
故答案为:第1,利用SAS得出全等三角形,即可配成与原来同样大小的一块.
【分析】利用SAS,进而得出全等的三角形,进而求出即可.
13.【答案】
2
【考点】全等三角形的性质
解:
,
,
运动时间相同,
,
的运动速度也相同,
.
故答案为
【分析】根据全等三角形的性质可知PA=BQ,根据路程、速度、时间之间的关系即可判断
三、解答题
14.【答案】
解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABD=∠CBE=132°÷2=66°.
又由△ABC≌△DBE,
∴AB=BD,∠A=∠BDE,
∴∠ADB=∠A=∠BDE=(180°-∠ABD)÷2=57°.
∴∠CDE=180°-∠ADB-∠BDE=66°.
【考点】全等三角形的性质
【解析】【分析】根据全等三角形的性质得到∠ABC=∠DBE,进而得出∠ABD=∠CBE,又由全等可得AB=BD,由等边对等角可得出∠ADB=∠A=∠BDE,最后可得出∠CDE的度数..
15.【答案】
证明:BF=CE,BF+FC=FC+CE,即BC=EF
AC//DF,
在△ABC和△DEF中
△ABC≌△DEF
【考点】三角形全等的判定
【解析】【分析】由题意用角角边可证△ABC≌△DEF.
16.【答案】
证明:∵∠B+∠AEC=180°,∠CED+∠AEC=180°
∴∠B=∠DEC
在△ABC和△DEC中
∴△ABC≌△DEC(AAS)
∴
【考点】余角、补角及其性质,三角形全等的判定
【解析】【分析】根据同角的补角相等,即可得到∠B=∠DEC,根据三角形的任意两个角及其一个角的对边相等,即可得到两个三角形全等,得出答案即可。
17.【答案】
解:∵∠1=∠2,
∴∠BAC=∠DAE.
∵∠1=∠3,
又∵∠ADC=∠1+∠B=∠3+∠ADE,
∴∠B=∠ADE.
在△ABC和△ADE中,
∴
【考点】三角形全等的判定
【解析】【分析】∠1=∠2可以推出∠BAC=∠DAE,根据外角定理可以推出∠B=∠ADE,再由AB=AD,即可证明.
18.【答案】
解:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,
∠ADC=∠E=90°,∠B=∠ACD,AC=BC,
∴△ACD≌△CBE(AAS).
【考点】三角形全等的判定
【解析】【分析】根据同角的余角相等得出
∠B=∠ACD,
从而利用AAS判断出
△ACD≌△CBE
。
19.【答案】
(1)∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB
,
由折叠的性质可知
AD=AF
,
∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF
,
∴∠AFG=∠B
,
又AG=AG
,
∴△ABG≌△AFG;
(2)∵△ABG≌△AFG
,
∴BG=FG
,
设BG=FG=
,则GC=
,
∵E为CD的中点,
∴CF=EF=DE=3,
∴EG=
,
∴
,
解得
,
∴BG=2
【考点】全等三角形的性质,勾股定理,翻折变换(折叠问题)
【解析】【分析】(1)根据正方形的性质以及折叠的性质即可得到证明三角形全等。
(2)根据全等三角形的性质,可以设BG=FG=x,根据勾股定理计算出x的值,得
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
