2020年秋人教版八年级数学上册暑期课程跟踪——11.2.1三角形的内角提优练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册暑期课程跟踪——11.2.1三角形的内角提优练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 23:22:49 | ||
图片预览


文档简介
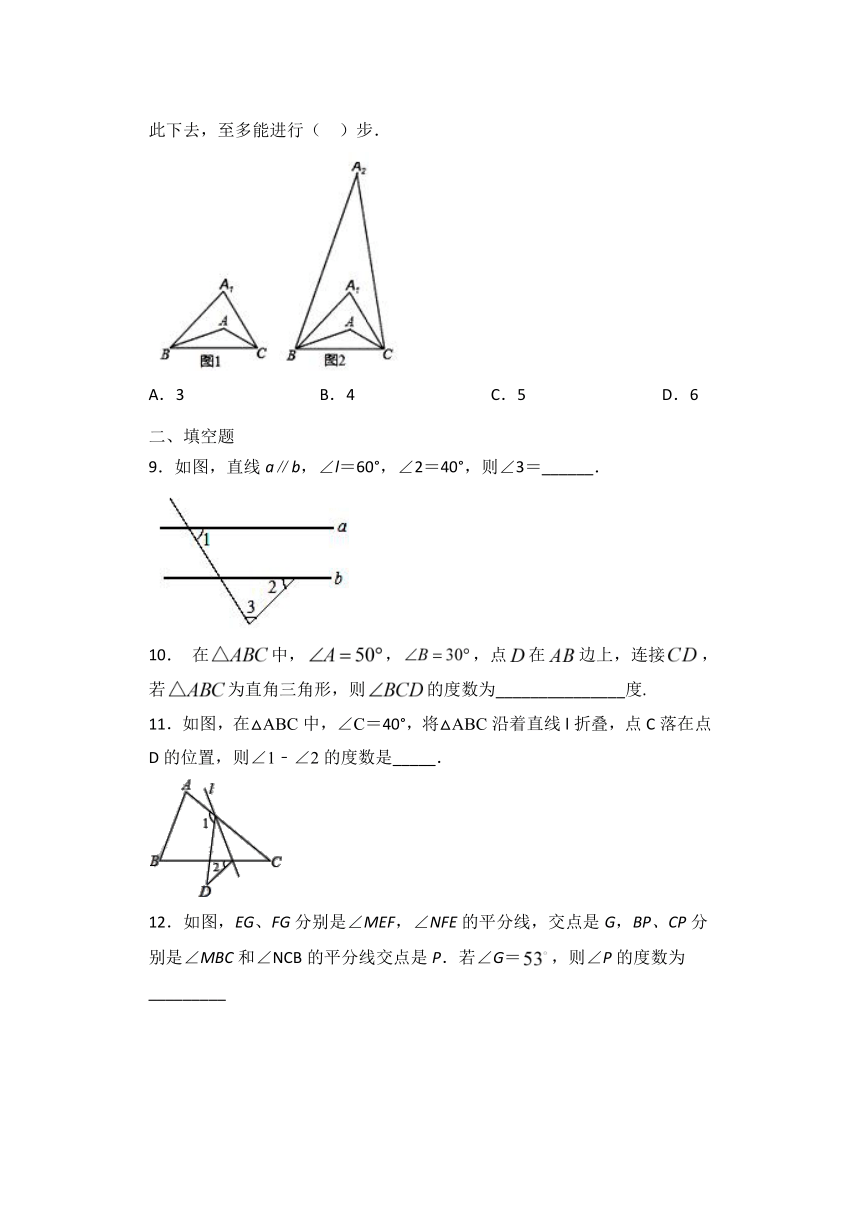
11.2.1三角形的内角提优练习
一、选择题
1.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDC=( )
A.120°
B.60°
C.140°
D.无法确定
2.已知,一张直角三角形纸片,,,.将纸片沿折叠(如图所示),点落在处,则的度数为( )
A.
B.
C.
D.67°
3.
三角形的内角和等于( )
A.
B.
C.
D.
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC为(
)
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
5.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
6.
如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是(
)
A.
B.
C.
D.
7.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( )
A.γ=2α+β
B.γ=α+2β
C.γ=α+β
D.γ=180°﹣α﹣β
8.在△ABC中,第一步:在△ABC上方确定一点,使,,如图第二步:在△A1BC上方确定一点,使,,如图照此下去,至多能进行( )步.
A.3
B.4
C.5
D.6
二、填空题
9.如图,直线a∥b,∠l=60°,∠2=40°,则∠3=______.
10.
在中,,,点在边上,连接,若为直角三角形,则的度数为_______________度.
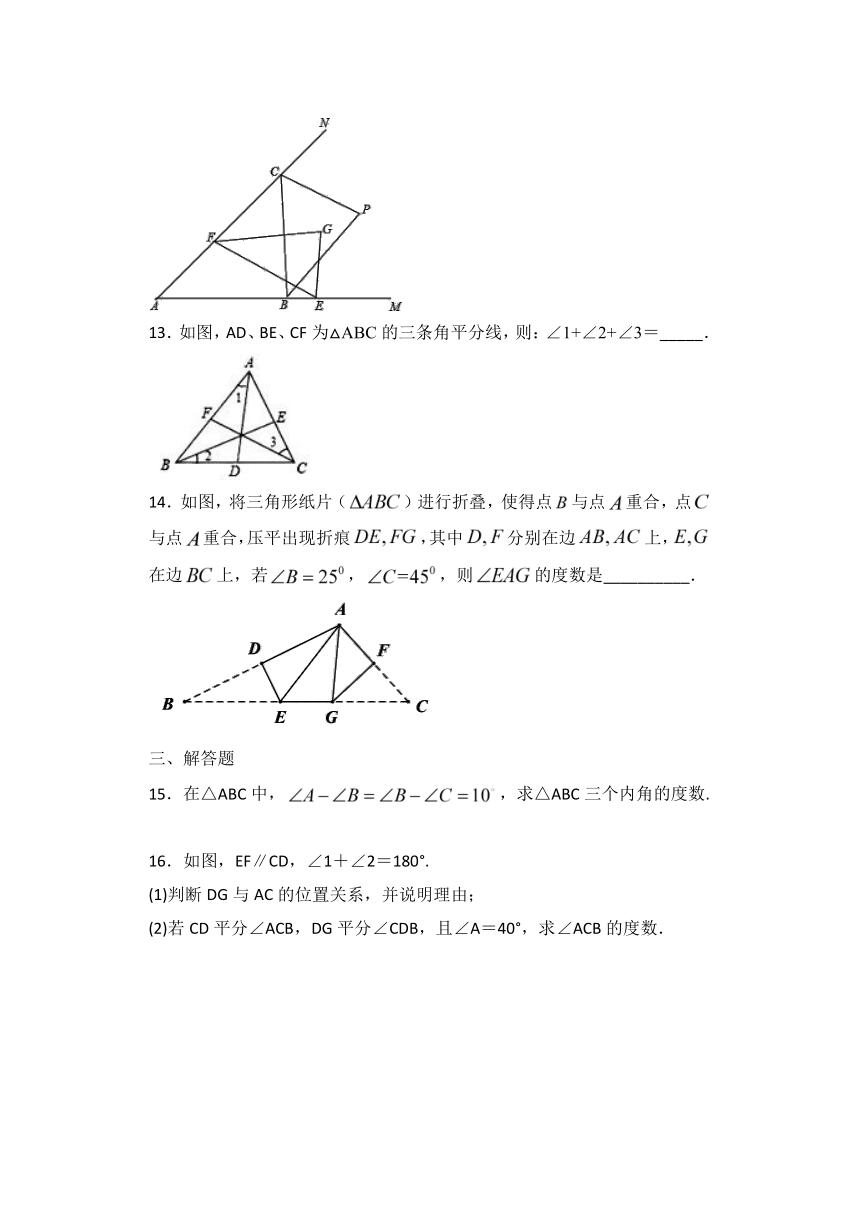
11.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是_____.
12.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP、CP分别是∠MBC和∠NCB的平分线交点是P.若∠G=,则∠P的度数为_________
13.如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=_____.
14.如图,将三角形纸片()进行折叠,使得点与点重合,点与点重合,压平出现折痕,其中分别在边上,在边上,若,,则的度数是__________.
三、解答题
15.在△ABC中,,求△ABC三个内角的度数.
16.如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
17.在△ABC中,,求△ABC三个内角的度数.
18.如图,BE和BF三等分∠ABC,CE和CF三等分∠ACB,∠A=60°,求∠BEC和∠BFC的度数.
19.如图,在中,,求的度数.
20.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
答案
1.
C
2.
A
3.
B
4.
B
5.
B
6.
B
7.
A
8.
B
9.
80°
10.
或
11.
12.
53
13.
90°
14.
40°
15.
解:∵∠A-∠B=∠B-∠C
∴∠A+∠C=2∠B
又∵∠A+∠B+∠C=180°
∴3∠B=180°
∴∠B=60°
又∵∠A-∠B=10°,∠B-∠C=10°
∴∠A=∠B+10°=70°
∠C=∠B-10°=50°
即ΔABC的三个内角的度数分别为70°,60°,50°.
16.
解:(1)AC∥DG.
理由:∵EF∥CD,
∴∠1+∠ACD=180°,
又∵∠1+∠2=180°,
∴∠ACD=∠2,
∴AC∥DG.
(2)∵AC∥DG,
∴∠BDG=∠A=40°,
∵DG平分∠CDB,
∴∠CDB=2∠BDG=80°,
∵∠BDC是△ACD的外角,
∴∠ACD=∠BDC-∠A=80°-40°=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
17.
解∵∠A-∠B=∠B-∠C
∴∠A+∠C=2∠B
又∵∠A+∠B+∠C=180°
∴3∠B=180°
∴∠B=60°
又∵∠A-∠B=10°,∠B-∠C=10°
∴∠A=∠B+10°=70°
∠C=∠B-10°=50°
即ΔABC的三个内角的度数分别为70°,60°,50°.
18.
解
如图,延长BE交AC于G,
由三角形外角性质,可得∠BEC=∠BGC+∠ACE,∠BGC=∠A+∠ABE,
∵BE和BF三等分∠ABC,CE和CF三等分∠ACB,
∴∠ABE=∠ABC,∠ACE=∠ACB,
又∵∠ABC+∠ACB=180°﹣∠A,
∴∠BEC=∠A+∠ABC+∠ACB=∠A+(180°﹣∠A)=60°+∠A,
当∠A=60°时,∠BEC=60°+×60°=100°,
同理可得,∠BFC=∠A+(180°﹣∠A)=120°+∠A=120°+×60°=140°.
19.
解:
.
∴在中,,
∵
∴.
∵在中,,
∴
.
20.
解:(1)∵∠A+∠B+∠C=180°,
∴∠A=180°﹣(∠B+∠C)=180°﹣(50°+60°)=70°.
(2)∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
∴∠A=×130°=65°.
一、选择题
1.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDC=( )
A.120°
B.60°
C.140°
D.无法确定
2.已知,一张直角三角形纸片,,,.将纸片沿折叠(如图所示),点落在处,则的度数为( )
A.
B.
C.
D.67°
3.
三角形的内角和等于( )
A.
B.
C.
D.
4.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC为(
)
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
5.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
6.
如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是(
)
A.
B.
C.
D.
7.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( )
A.γ=2α+β
B.γ=α+2β
C.γ=α+β
D.γ=180°﹣α﹣β
8.在△ABC中,第一步:在△ABC上方确定一点,使,,如图第二步:在△A1BC上方确定一点,使,,如图照此下去,至多能进行( )步.
A.3
B.4
C.5
D.6
二、填空题
9.如图,直线a∥b,∠l=60°,∠2=40°,则∠3=______.
10.
在中,,,点在边上,连接,若为直角三角形,则的度数为_______________度.
11.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是_____.
12.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP、CP分别是∠MBC和∠NCB的平分线交点是P.若∠G=,则∠P的度数为_________
13.如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=_____.
14.如图,将三角形纸片()进行折叠,使得点与点重合,点与点重合,压平出现折痕,其中分别在边上,在边上,若,,则的度数是__________.
三、解答题
15.在△ABC中,,求△ABC三个内角的度数.
16.如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
17.在△ABC中,,求△ABC三个内角的度数.
18.如图,BE和BF三等分∠ABC,CE和CF三等分∠ACB,∠A=60°,求∠BEC和∠BFC的度数.
19.如图,在中,,求的度数.
20.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
答案
1.
C
2.
A
3.
B
4.
B
5.
B
6.
B
7.
A
8.
B
9.
80°
10.
或
11.
12.
53
13.
90°
14.
40°
15.
解:∵∠A-∠B=∠B-∠C
∴∠A+∠C=2∠B
又∵∠A+∠B+∠C=180°
∴3∠B=180°
∴∠B=60°
又∵∠A-∠B=10°,∠B-∠C=10°
∴∠A=∠B+10°=70°
∠C=∠B-10°=50°
即ΔABC的三个内角的度数分别为70°,60°,50°.
16.
解:(1)AC∥DG.
理由:∵EF∥CD,
∴∠1+∠ACD=180°,
又∵∠1+∠2=180°,
∴∠ACD=∠2,
∴AC∥DG.
(2)∵AC∥DG,
∴∠BDG=∠A=40°,
∵DG平分∠CDB,
∴∠CDB=2∠BDG=80°,
∵∠BDC是△ACD的外角,
∴∠ACD=∠BDC-∠A=80°-40°=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
17.
解∵∠A-∠B=∠B-∠C
∴∠A+∠C=2∠B
又∵∠A+∠B+∠C=180°
∴3∠B=180°
∴∠B=60°
又∵∠A-∠B=10°,∠B-∠C=10°
∴∠A=∠B+10°=70°
∠C=∠B-10°=50°
即ΔABC的三个内角的度数分别为70°,60°,50°.
18.
解
如图,延长BE交AC于G,
由三角形外角性质,可得∠BEC=∠BGC+∠ACE,∠BGC=∠A+∠ABE,
∵BE和BF三等分∠ABC,CE和CF三等分∠ACB,
∴∠ABE=∠ABC,∠ACE=∠ACB,
又∵∠ABC+∠ACB=180°﹣∠A,
∴∠BEC=∠A+∠ABC+∠ACB=∠A+(180°﹣∠A)=60°+∠A,
当∠A=60°时,∠BEC=60°+×60°=100°,
同理可得,∠BFC=∠A+(180°﹣∠A)=120°+∠A=120°+×60°=140°.
19.
解:
.
∴在中,,
∵
∴.
∵在中,,
∴
.
20.
解:(1)∵∠A+∠B+∠C=180°,
∴∠A=180°﹣(∠B+∠C)=180°﹣(50°+60°)=70°.
(2)∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,
∴∠A=×130°=65°.
