2020年秋人教版八年级数学上册暑期课程跟踪——11.2.2三角形的外角提优练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册暑期课程跟踪——11.2.2三角形的外角提优练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 23:26:57 | ||
图片预览


文档简介
11.2.2三角形的外角提优练习
一、选择题
1.如图,已知,是它的一个外角,点E为边AC上一点,点D在边BC的延长线上,连接DE,则下列结论中不一定成立的是(
)
A.
B.
C.
D.
2.如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )
A.110°
B.120°
C.130°
D.150°
3.三角形的一个外角小于与它相邻的内角,这个三角形是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不确定
4.
如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
5.如图,∠A,∠1,∠2的大小关系是(
)
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
6.
如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
7.如图所示,,则下列各式等于的是(
)
A.
B.
C.
D.
8.
小桐把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于(
)
A.150°
B.180°
C.210°
D.270°
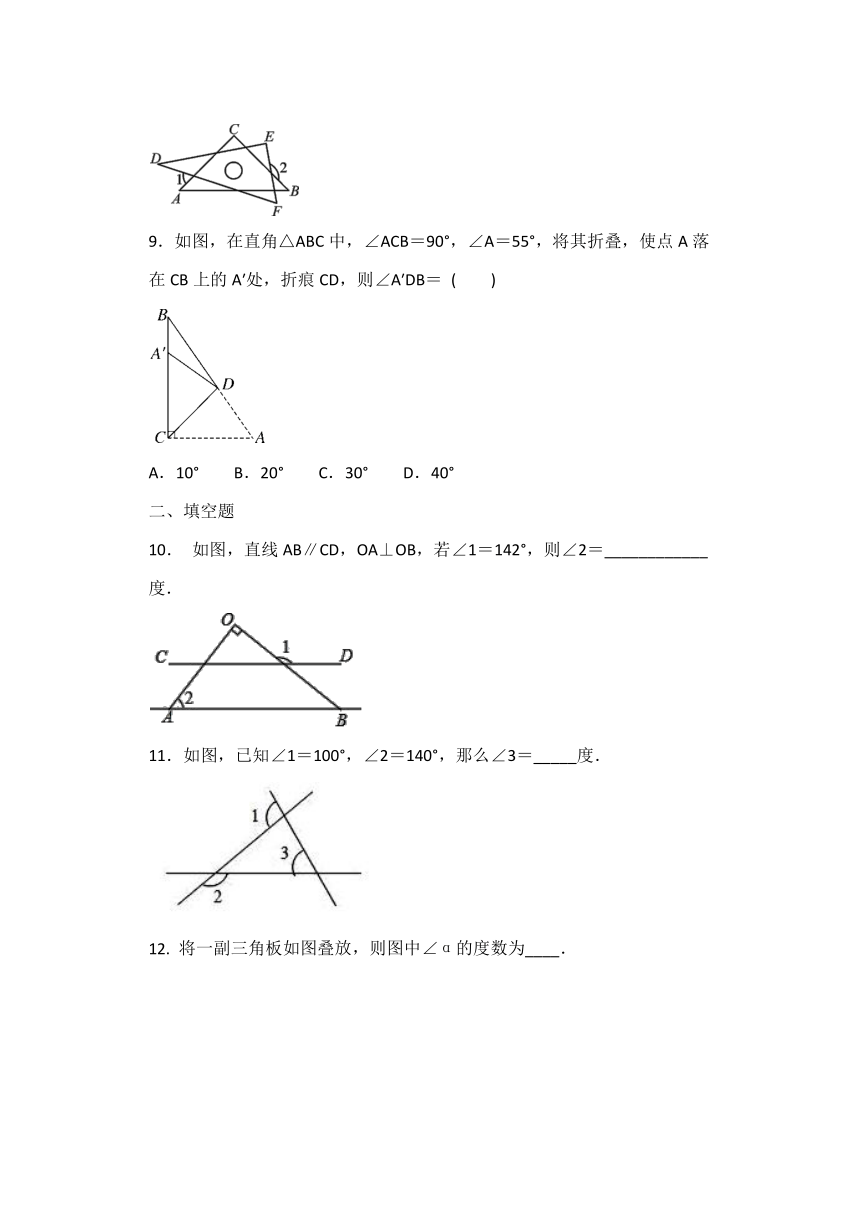
9.如图,在直角△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在CB上的A′处,折痕CD,则∠A′DB=
( )
A.10°
B.20°
C.30°
D.40°
二、填空题
10.
如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=____________度.
11.如图,已知∠1=100°,∠2=140°,那么∠3=_____度.
12.
将一副三角板如图叠放,则图中∠α的度数为____.
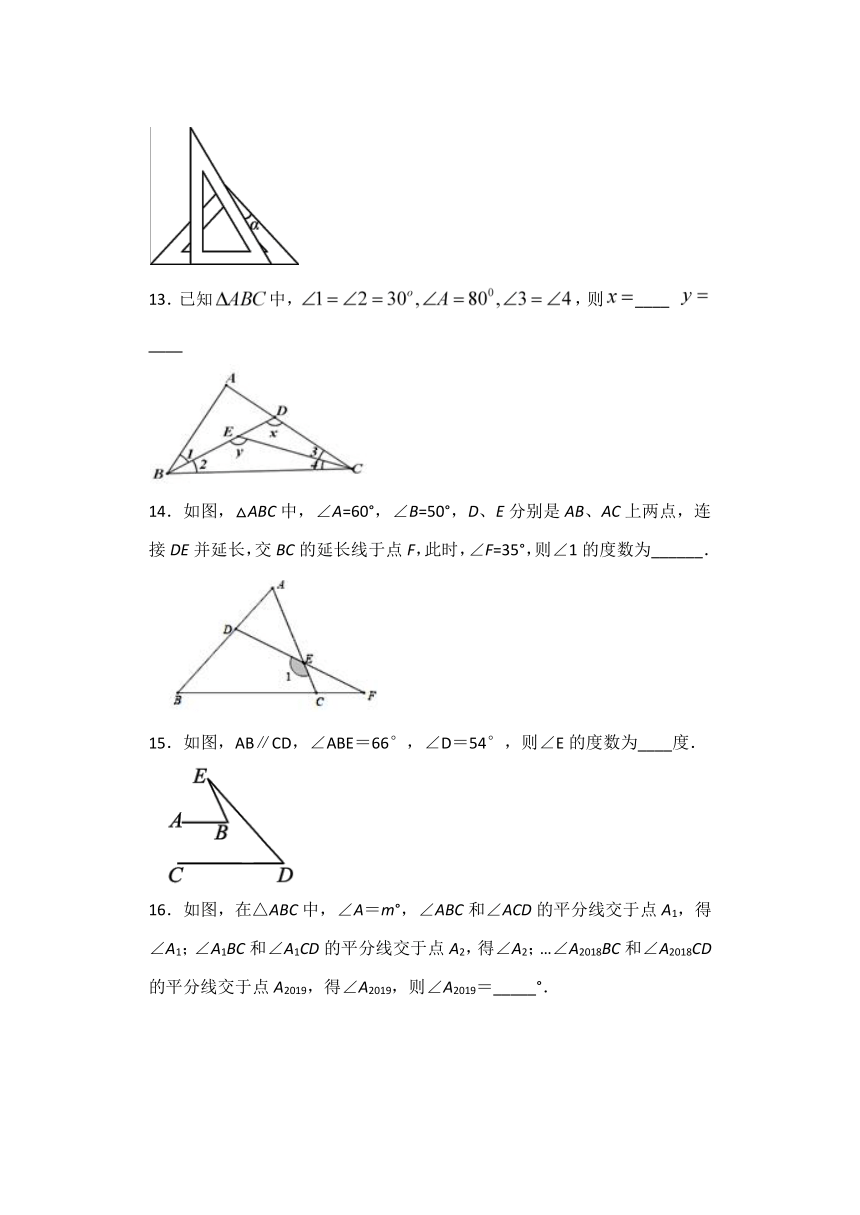
13.已知中,,则____
____
14.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为______.
15.如图,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为____度.
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.
17.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB= ____ .
三、解答题
18.如图,在中,D是BC边上一点,,,求的度数.
19.己知:如图,,和相交于点,是上一点,是上一点,且.
(1)求证:;
(2)若,,求的度数.
20.如图,将△MNP的三边分别向两边延长,并在每两条延长线上任取两点连接起来,又得到了三个新的三角形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
21.
如图,已知DE分别交△ABC的边AB,AC于D,E,交BC的延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.
22.
(1)如图①,点P为△ABC的∠ABC和∠ACB的角平分线的交点,求证:∠P=90°+∠A;
(2)如图②,点P为△ABC的∠ABC和外角∠ACE的角平分线的交点,求证:∠P=∠A;
(3)如图③,点P为△ABC的外角∠CBE和∠BCF的角平分线的交点,求证:∠P=90°-∠A.
答案
1.
D
2.
D
3.
B
4.
B
5.
B
6.
B
7.
D
8.
C
9.
B
10.
52
11.
60°
12.
15°
13.
110°
130°
14.
145°
15.
12
16.
17.
700
18.
解∵∠1=∠2=39°,
∴∠3=∠4=∠1+∠2=78°,
∴△ACD中,∠DAC=180°﹣(∠3+∠4)=180°﹣2×78°=24°.
19.
解(1)证明:,
,
,
,
;
(2)解:,
,
,
,
是的外角,
,
,
.
20.
证明:如图
∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
∴∠1+∠2+∠3=∠A+∠B+∠C+∠D+∠E+∠F.
又∵∠1=∠4+∠5,∠2=∠4+∠6,∠3=∠5+∠6,
∴∠1+∠2+∠3=∠4+∠5+∠4+∠6+∠5+∠6
=2(∠4+∠5+∠6)
=2×180°=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
21.
解:∠A=180°-∠B-∠ACB=180°-67°-74°=39°,
∴∠BDF=∠A+∠AED=39°+48°=87°
22.
解:(1)∠P=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A
(2)∠P=∠PCE-∠PBE=(∠ACE-∠ABC)=∠A
(3)∠P=180°-(∠PBC+∠PCB)
=180°-(∠EBC+∠FCB)
=180°-(∠A+∠ACB+∠FCB)
=180°-(∠A+180°)
=90°-∠A
一、选择题
1.如图,已知,是它的一个外角,点E为边AC上一点,点D在边BC的延长线上,连接DE,则下列结论中不一定成立的是(
)
A.
B.
C.
D.
2.如图,∠BCD=150°,则∠A+∠B+∠D的度数为( )
A.110°
B.120°
C.130°
D.150°
3.三角形的一个外角小于与它相邻的内角,这个三角形是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不确定
4.
如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
5.如图,∠A,∠1,∠2的大小关系是(
)
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
6.
如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是(
)
A.15°
B.30°
C.45°
D.60°
7.如图所示,,则下列各式等于的是(
)
A.
B.
C.
D.
8.
小桐把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于(
)
A.150°
B.180°
C.210°
D.270°
9.如图,在直角△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在CB上的A′处,折痕CD,则∠A′DB=
( )
A.10°
B.20°
C.30°
D.40°
二、填空题
10.
如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=____________度.
11.如图,已知∠1=100°,∠2=140°,那么∠3=_____度.
12.
将一副三角板如图叠放,则图中∠α的度数为____.
13.已知中,,则____
____
14.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为______.
15.如图,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为____度.
16.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.
17.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB= ____ .
三、解答题
18.如图,在中,D是BC边上一点,,,求的度数.
19.己知:如图,,和相交于点,是上一点,是上一点,且.
(1)求证:;
(2)若,,求的度数.
20.如图,将△MNP的三边分别向两边延长,并在每两条延长线上任取两点连接起来,又得到了三个新的三角形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
21.
如图,已知DE分别交△ABC的边AB,AC于D,E,交BC的延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.
22.
(1)如图①,点P为△ABC的∠ABC和∠ACB的角平分线的交点,求证:∠P=90°+∠A;
(2)如图②,点P为△ABC的∠ABC和外角∠ACE的角平分线的交点,求证:∠P=∠A;
(3)如图③,点P为△ABC的外角∠CBE和∠BCF的角平分线的交点,求证:∠P=90°-∠A.
答案
1.
D
2.
D
3.
B
4.
B
5.
B
6.
B
7.
D
8.
C
9.
B
10.
52
11.
60°
12.
15°
13.
110°
130°
14.
145°
15.
12
16.
17.
700
18.
解∵∠1=∠2=39°,
∴∠3=∠4=∠1+∠2=78°,
∴△ACD中,∠DAC=180°﹣(∠3+∠4)=180°﹣2×78°=24°.
19.
解(1)证明:,
,
,
,
;
(2)解:,
,
,
,
是的外角,
,
,
.
20.
证明:如图
∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
∴∠1+∠2+∠3=∠A+∠B+∠C+∠D+∠E+∠F.
又∵∠1=∠4+∠5,∠2=∠4+∠6,∠3=∠5+∠6,
∴∠1+∠2+∠3=∠4+∠5+∠4+∠6+∠5+∠6
=2(∠4+∠5+∠6)
=2×180°=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
21.
解:∠A=180°-∠B-∠ACB=180°-67°-74°=39°,
∴∠BDF=∠A+∠AED=39°+48°=87°
22.
解:(1)∠P=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A
(2)∠P=∠PCE-∠PBE=(∠ACE-∠ABC)=∠A
(3)∠P=180°-(∠PBC+∠PCB)
=180°-(∠EBC+∠FCB)
=180°-(∠A+∠ACB+∠FCB)
=180°-(∠A+180°)
=90°-∠A
