2020年秋人教版八年级数学上册暑期课程跟踪——11.2与三角形有关的角提优练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册暑期课程跟踪——11.2与三角形有关的角提优练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 23:25:05 | ||
图片预览


文档简介
11.2与三角形有关的角提优练习
一、选择题
1.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:5:6,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
2.如图,已知,直角三角板的直角顶点在直线上,若,则下列结论正确的是(
)
A.
B.
C.
D.
3.关于三角形内角的叙述错误的是
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
4.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B是( )
A.45°
B.55°
C.65°
D.75°
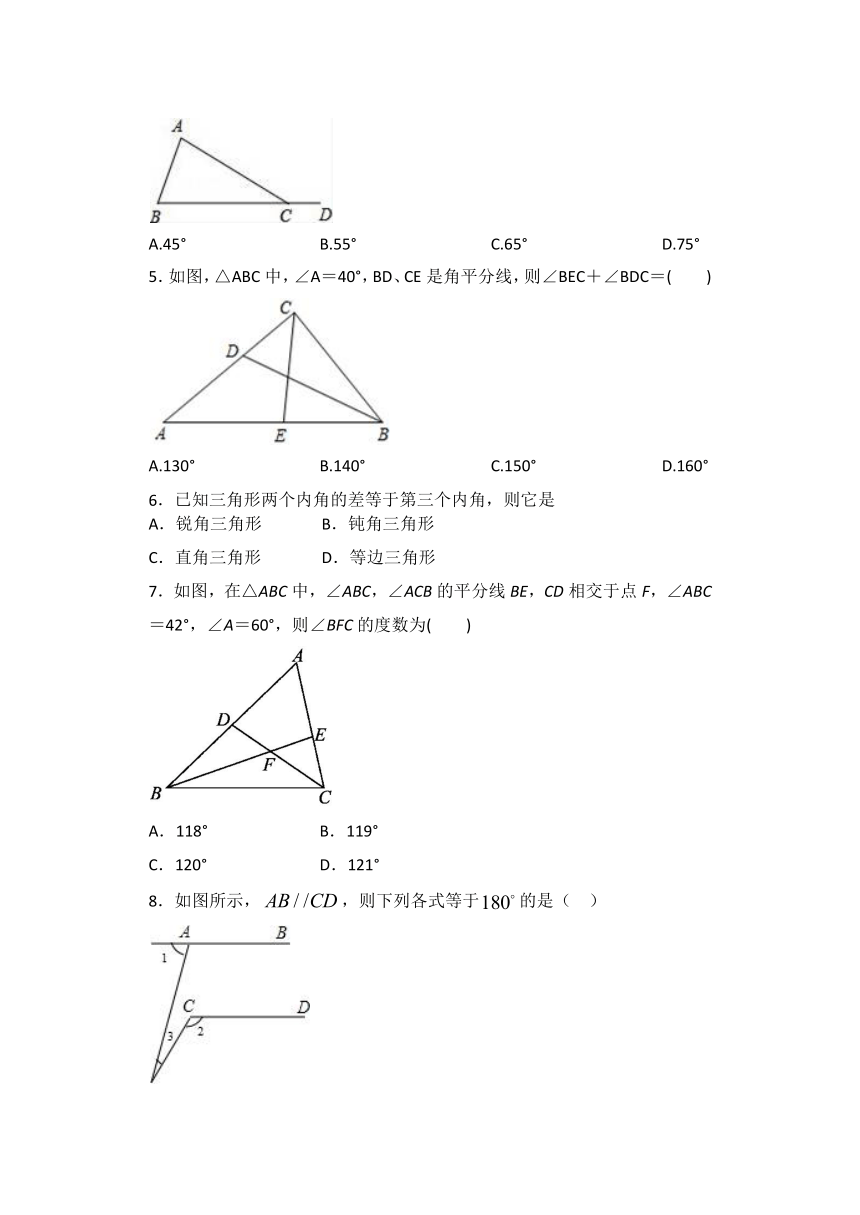
5.如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=(
)
A.130°
B.140°
C.150°
D.160°
6.已知三角形两个内角的差等于第三个内角,则它是
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
7.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118°
B.119°
C.120°
D.121°
8.如图所示,,则下列各式等于的是(
)
A.
B.
C.
D.
9.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于
A.25°
B.30°
C.35°
D.40°
二、填空题
10.等腰三角形一腰上的高与另一腰的夹角为50°,则这个等腰三角形的底角度数为__________.
11.将一副直角三角尺按如图所示摆放,则图中的度数是______.
12.在△ABC中,∠B、∠C的平分线相交于点O,若∠A=40°,则∠BOC=_____度.
13.若△ABC为钝角三角形,且∠A=50°,则∠B的取值范围为____.
14.如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A=___________.
三、解答题
15.如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
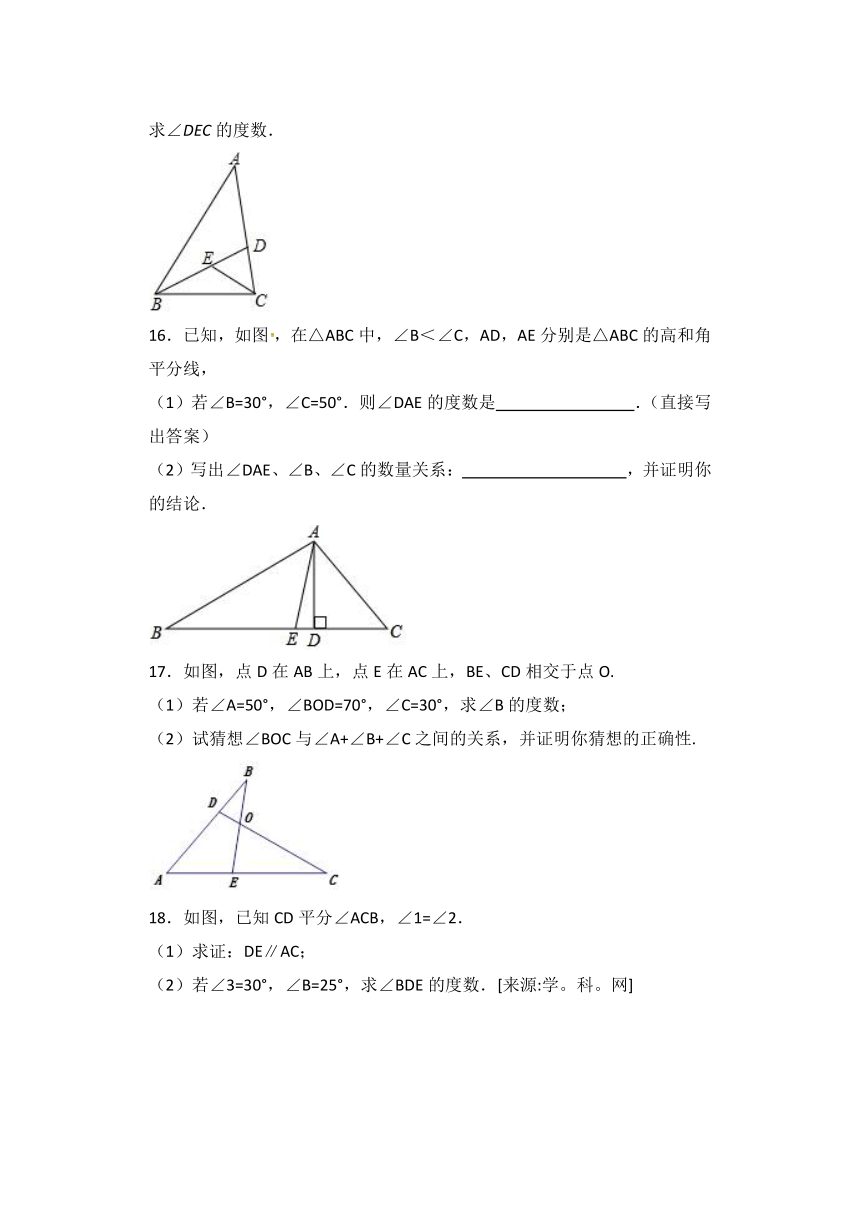
16.已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是
.(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系:
,并证明你的结论.
17.如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
18.如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.[来源:学。科。网]
19.如图,AD是△ABC边上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
20.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与
∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.则:
(1)求∠A1的度数;
(2)∠An的度数.
答案
1.
D
2.
D
3.
B
4.
C
5.
C
6.
C
7.
C
8.
D
9.
D
10.
70°或20°
11.
12.
110°
13.130°>∠B>90°或0°<∠B<40°.
14.
50°
15.
在△ABC中,∵∠A=55°,∠ACB=70°,
∴∠ABC=55°,
∵∠ABD=32°,
∴∠CBD=∠ABC-∠ABD=23°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=35°,
∴在△BCE中,∠DEC=∠CBD+∠BCE=58°.
16.
(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
又∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=50°,
∵AD是△ABC的高,
∴∠BAD=90°-∠B=90°-30°=60°,
则∠DAE=∠BAD-∠BAE=10°,
故答案为:10°;
(2)∠DAE=(∠C-∠B),
理由如下:∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵AE是△ABC的角平分线,
∴∠EAC=∠BAC,
∵∠BAC=180°-∠B-∠C
∴∠DAE=∠EAC-∠DAC,
=∠BAC-(90°-∠C),
=(180°-∠B-∠C)-90°+∠C,
=90°-∠B-∠C-90°+∠C,
=(∠C-∠B).
故答案为:(∠C-∠B).
17.
解:(1)∵∠A=50°,∠C=30°,∴∠BDO=80°;∵∠BOD=70°,∴∠B=30°;
(2)∠BOC=∠A+∠B+∠C.
理由:∵∠BOC=∠BEC
+∠C,∠BEC=∠A+∠B,
∴∠BOC=∠A+∠B+∠C.
18.
(1)证明:∵CD平分∠ACB,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠3,
∴DE∥AC;
(2)解:∵CD平分∠ACB,∠3=30°,
∴∠ACB=2∠3=60°.
∵DE∥AC,
∴∠BED=∠ACB=60°.
∵∠B=25°,
∴∠BDE=180°-60°-25°=95°
19.
∵AD是△ABC的高,∴∠ADB=90°,
又∵,∠BED=70°,
∴.
∵BE平分∠ABC,∴∠ABC=2∠DBE=40°.
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,∴∠BAC=180°–∠ABC–∠C=80°.
20.
(1)∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=θ,
∴∠A1=.
(2)同理可得∠A2=∠A1=·=,
所以∠An=.
一、选择题
1.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:5:6,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
2.如图,已知,直角三角板的直角顶点在直线上,若,则下列结论正确的是(
)
A.
B.
C.
D.
3.关于三角形内角的叙述错误的是
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
4.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B是( )
A.45°
B.55°
C.65°
D.75°
5.如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=(
)
A.130°
B.140°
C.150°
D.160°
6.已知三角形两个内角的差等于第三个内角,则它是
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
7.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118°
B.119°
C.120°
D.121°
8.如图所示,,则下列各式等于的是(
)
A.
B.
C.
D.
9.如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于
A.25°
B.30°
C.35°
D.40°
二、填空题
10.等腰三角形一腰上的高与另一腰的夹角为50°,则这个等腰三角形的底角度数为__________.
11.将一副直角三角尺按如图所示摆放,则图中的度数是______.
12.在△ABC中,∠B、∠C的平分线相交于点O,若∠A=40°,则∠BOC=_____度.
13.若△ABC为钝角三角形,且∠A=50°,则∠B的取值范围为____.
14.如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A=___________.
三、解答题
15.如图,在△ABC中,∠A=55°,∠ABD=32°,∠ACB=70°,且CE平分∠ACB,求∠DEC的度数.
16.已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是
.(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系:
,并证明你的结论.
17.如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.
18.如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.[来源:学。科。网]
19.如图,AD是△ABC边上的高,BE平分∠△ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
20.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与
∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.则:
(1)求∠A1的度数;
(2)∠An的度数.
答案
1.
D
2.
D
3.
B
4.
C
5.
C
6.
C
7.
C
8.
D
9.
D
10.
70°或20°
11.
12.
110°
13.130°>∠B>90°或0°<∠B<40°.
14.
50°
15.
在△ABC中,∵∠A=55°,∠ACB=70°,
∴∠ABC=55°,
∵∠ABD=32°,
∴∠CBD=∠ABC-∠ABD=23°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=35°,
∴在△BCE中,∠DEC=∠CBD+∠BCE=58°.
16.
(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
又∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=50°,
∵AD是△ABC的高,
∴∠BAD=90°-∠B=90°-30°=60°,
则∠DAE=∠BAD-∠BAE=10°,
故答案为:10°;
(2)∠DAE=(∠C-∠B),
理由如下:∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵AE是△ABC的角平分线,
∴∠EAC=∠BAC,
∵∠BAC=180°-∠B-∠C
∴∠DAE=∠EAC-∠DAC,
=∠BAC-(90°-∠C),
=(180°-∠B-∠C)-90°+∠C,
=90°-∠B-∠C-90°+∠C,
=(∠C-∠B).
故答案为:(∠C-∠B).
17.
解:(1)∵∠A=50°,∠C=30°,∴∠BDO=80°;∵∠BOD=70°,∴∠B=30°;
(2)∠BOC=∠A+∠B+∠C.
理由:∵∠BOC=∠BEC
+∠C,∠BEC=∠A+∠B,
∴∠BOC=∠A+∠B+∠C.
18.
(1)证明:∵CD平分∠ACB,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠3,
∴DE∥AC;
(2)解:∵CD平分∠ACB,∠3=30°,
∴∠ACB=2∠3=60°.
∵DE∥AC,
∴∠BED=∠ACB=60°.
∵∠B=25°,
∴∠BDE=180°-60°-25°=95°
19.
∵AD是△ABC的高,∴∠ADB=90°,
又∵,∠BED=70°,
∴.
∵BE平分∠ABC,∴∠ABC=2∠DBE=40°.
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,∴∠BAC=180°–∠ABC–∠C=80°.
20.
(1)∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=θ,
∴∠A1=.
(2)同理可得∠A2=∠A1=·=,
所以∠An=.
