沪科版初中数学九年级上册第21章《二次函数与反比例函数》综合测试(Word版 含答案)
文档属性
| 名称 | 沪科版初中数学九年级上册第21章《二次函数与反比例函数》综合测试(Word版 含答案) | 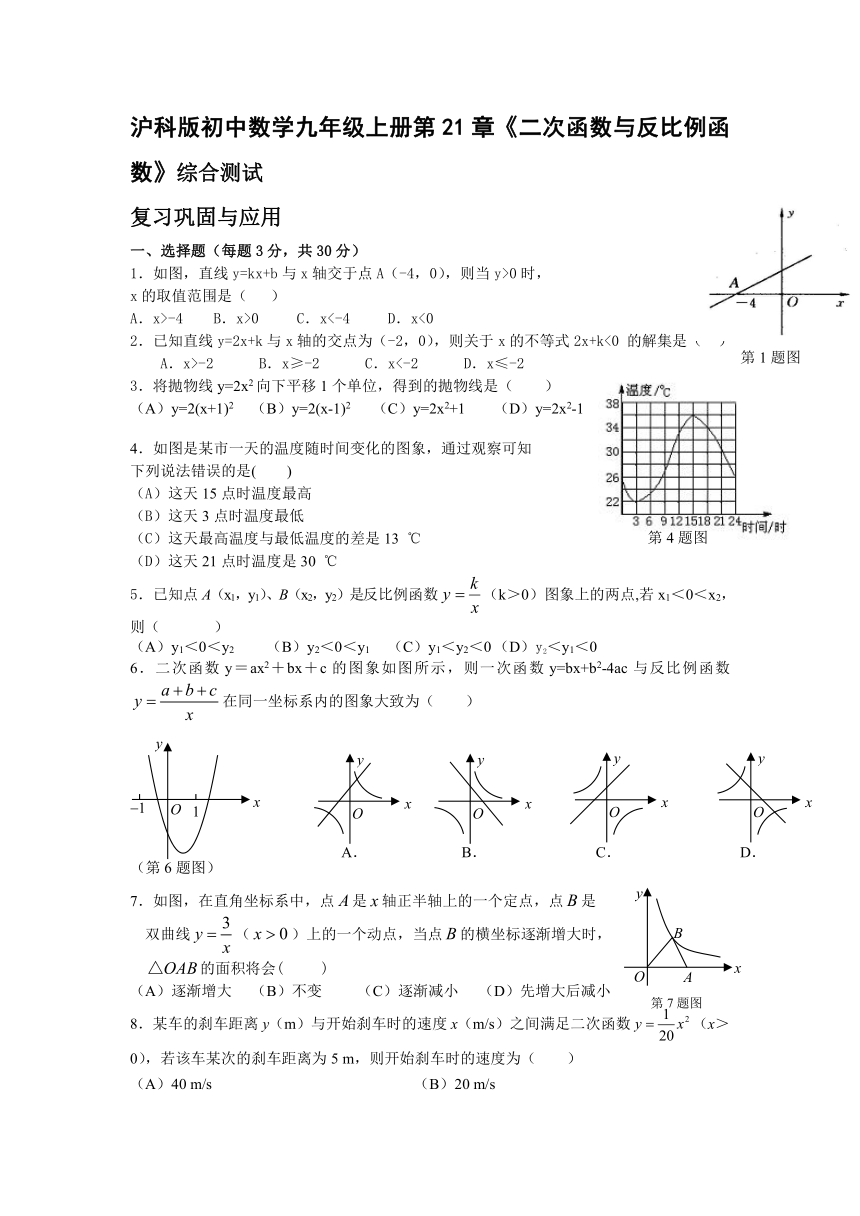 | |
| 格式 | zip | ||
| 文件大小 | 482.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 22:59:28 | ||
图片预览



文档简介
沪科版初中数学九年级上册第21章《二次函数与反比例函数》综合测试
复习巩固与应用
一、选择题(每题3分,共30分)
1.如图,直线y=kx+b与x轴交于点A(-4,0),则当y>0时,
x的取值范围是(
)
A.x>-4
B.x>0
C.x<-4
D.x<0
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于x的不等式2x+k<0的解集是(
)
A.x>-2
B.x≥-2
C.x<-2
D.x≤-2
3.将抛物线y=2x2向下平移1个单位,得到的抛物线是( )
(A)y=2(x+1)2
(B)y=2(x-1)2
(C)y=2x2+1
(D)y=2x2-1
4.如图是某市一天的温度随时间变化的图象,通过观察可知
下列说法错误的是(
)
(A)这天15点时温度最高
(B)这天3点时温度最低
(C)这天最高温度与最低温度的差是13
℃
(D)这天21点时温度是30
℃
5.已知点A(x1,y1)、B(x2,y2)是反比例函数(k>0)图象上的两点,若x1<0<x2,
则(
)
(A)y1<0<y2
(B)y2<0<y1
(C)y1<y2<0
(D)y2<y1<0
6.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数在同一坐标系内的图象大致为(
)
7.如图,在直角坐标系中,点是轴正半轴上的一个定点,点是
双曲线()上的一个动点,当点的横坐标逐渐增大时,
的面积将会(
)
(A)逐渐增大
(B)不变
(C)逐渐减小
(D)先增大后减小
8.某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数(x>0),若该车某次的刹车距离为5
m,则开始刹车时的速度为(
)
(A)40
m/s
(B)20
m/s
(C)10
m/s
(D)5
m/s
9.一次函数y=kx+b与反比例函数y=kx的图象如图所示,
则下列说法正确的是?( )
(A)它们的函数值y随着x的增大而增大?
(B)它们的函数值y随着x的增大而减小?
(C)k<0?
(D)它们的自变量x的取值为全体实数?
10.已知二次函数y=ax2+bx+c的与的部分对应值如下表:
x
……
-1
0
1
3
……
y
……
-3
1
3
1
……
则下列判断中正确的是( )
(A)抛物线开口向上 (B)抛物线与轴交于负半轴
(C)当=4时,>0
(D)方程ax2+bx+c=0的正根在3与4之间
二、填空题(每题3分,共30分)
11.一个长方形周长为12,一边长为,面积随的变化而变化,则与的关系式是_________.当时,_________.
12.下列函数:①y=-x;②y=2x;③;④y=x2.当x<0
时,y随x的增大而减小的函数有
个
13.把抛物线y=ax+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x-3x+5,则a+b+c=__________
14.从地面垂直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的函数关系式是h=9.8t-4.9t2,那么小球运动中的最大高度为
米.
15.如图所示,抛物线y=ax2+bx+c()与轴的两个交点分别为A(-1,0)和B(2,0),当y<0
时,x的取值范围是
.
16.出售某种文具盒,若每个获利x元,一天可售出(6-x)个,则当
元时,一天出售该种文具盒的总利润y最大.
17.若梯形的下底长为x,上底长为下底长的,高为y,面积为60,则y与x的函数关系是____________.(不考虑的取值范围)
18.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数
(x>0)的图象上,则点E的坐标是___
19.如图,函数y=x与的图象交于A、B两点,过点A作AC垂直于y轴,垂足为C,则的面积为
.
20.如图,为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中,正确的说法有
.(请写出所有正确说法的序号)
三、解答题(每题10分,共60分)
21.下表是佳佳往妹妹家打长途电话的几次收费记载:
时间/分
1
2
3
4
5
6
7
电话费/元
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)你能帮佳佳预测一下,如果她打电话用时间是10分钟,则需付多少电话费?
22.已知关于x的一元二次方程2x2+4x+k-1=0有实数根,为正整数
(1)求的值;
(2)当此方程有两个非零的整数根时,将关于的二次函数y=2x2+4x+k-1的图象向下平移8个单位,求平移后的图象的解析式;
23.为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例;药物释放完毕后,与成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,与之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
24.如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数
(k为常数,)的图象相交于点
A(1,3).
(1)求这两个函数的解析式及其图象的另一交点的坐标;
(2)观察图象,写出使函数值y1≥y2的自变量的取值范围.
四、拓广探索(10分)
25.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
选做题
26.如图,已知抛物线与轴的两个交点为,与y轴交于点.
(1)求三点的坐标;
(2)求证:是直角三角形;
(3)若坐标平面内的点,使得以点和三点为顶点的四边形是平行四边形,求点的坐标.(直接写出点的坐标,不必写求解过程)
参考答案:
一、1.A;2.C;3、D;4.C;5、A;6、D;7、C;8、C;9、C;10、D;
二、11.;12、2;13、11;14、4.9;15、或;
16、3;17、;18、(,);19、4;20、①②④;
三、21.(1)通话时间与电话费;其中通话时间是自变量,电话费是因变量;(2)6元.
22、解:(1)由题意得,.∴.∵为正整数,∴.
(2)当时,方程有一个根为零;
当时,方程无整数根;
当时,方程有两个非零的整数根.
综上所述,和不合题意,舍去;符合题意.
当时,二次函数为,把它的图象向下平移8个单位得到的图象的解析式为.
23、解:(1)药物释放过程中与的函数关系式为(0≤≤12),药物释放完毕后与的函数关系式为(≥12)
(2)
解之,得
(分钟)(小时),
答:
从药物释放开始,至少需要经过4小时后,学生才能进入教室.
24、解:(1)由题意,得,解得,所以一次函数的解析式为.
由题意,得,解得,所以反比例函数的解析式为.
由题意,得,解得.当时,,所以交点.)
(2)由图象可知,当或时,函数值.
25、解:(1)根据题意得解得.
所求一次函数的表达式为.
(2),
抛物线的开口向下,当时,随的增大而增大,而,
当时,.
当销售单价定为87元时,商场可获得最大利润,最大利润是891元.
(3)由,得,
整理得,,解得,.
由图象可知,要使该商场获得利润不低于500元,销售单价应在70元到110元之间,而,所以,销售单价的范围是.
26、(1)解:令,得,得点.
令,得,解得,
∴.
(2)法一:证明:因为,
,
∴,
∴是直角三角形.
法二:因为,∴,
∴,又,∴.
∴,∴,
∴,即是直角三角形.
(3),,.
第1题图
第4题图
x
y
O
A
B
第7题图
1
O
x
y
(第6题图)
y
x
O
y
x
O
B.
C.
y
x
O
A.
y
x
O
D.
第9题图
O
A
C
B
x
y
第20题图
第19题图
第18题图
第15题图
O
9
(毫克)
12
(分钟)
第23题图
y
x
B
1
2
3
3
1
2
A(1,3)
第24题图
O
A
B
x
y
C
第26题图
O
A
B
x
y
C
26题图
N
M2
M1
M3
复习巩固与应用
一、选择题(每题3分,共30分)
1.如图,直线y=kx+b与x轴交于点A(-4,0),则当y>0时,
x的取值范围是(
)
A.x>-4
B.x>0
C.x<-4
D.x<0
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于x的不等式2x+k<0的解集是(
)
A.x>-2
B.x≥-2
C.x<-2
D.x≤-2
3.将抛物线y=2x2向下平移1个单位,得到的抛物线是( )
(A)y=2(x+1)2
(B)y=2(x-1)2
(C)y=2x2+1
(D)y=2x2-1
4.如图是某市一天的温度随时间变化的图象,通过观察可知
下列说法错误的是(
)
(A)这天15点时温度最高
(B)这天3点时温度最低
(C)这天最高温度与最低温度的差是13
℃
(D)这天21点时温度是30
℃
5.已知点A(x1,y1)、B(x2,y2)是反比例函数(k>0)图象上的两点,若x1<0<x2,
则(
)
(A)y1<0<y2
(B)y2<0<y1
(C)y1<y2<0
(D)y2<y1<0
6.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数在同一坐标系内的图象大致为(
)
7.如图,在直角坐标系中,点是轴正半轴上的一个定点,点是
双曲线()上的一个动点,当点的横坐标逐渐增大时,
的面积将会(
)
(A)逐渐增大
(B)不变
(C)逐渐减小
(D)先增大后减小
8.某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数(x>0),若该车某次的刹车距离为5
m,则开始刹车时的速度为(
)
(A)40
m/s
(B)20
m/s
(C)10
m/s
(D)5
m/s
9.一次函数y=kx+b与反比例函数y=kx的图象如图所示,
则下列说法正确的是?( )
(A)它们的函数值y随着x的增大而增大?
(B)它们的函数值y随着x的增大而减小?
(C)k<0?
(D)它们的自变量x的取值为全体实数?
10.已知二次函数y=ax2+bx+c的与的部分对应值如下表:
x
……
-1
0
1
3
……
y
……
-3
1
3
1
……
则下列判断中正确的是( )
(A)抛物线开口向上 (B)抛物线与轴交于负半轴
(C)当=4时,>0
(D)方程ax2+bx+c=0的正根在3与4之间
二、填空题(每题3分,共30分)
11.一个长方形周长为12,一边长为,面积随的变化而变化,则与的关系式是_________.当时,_________.
12.下列函数:①y=-x;②y=2x;③;④y=x2.当x<0
时,y随x的增大而减小的函数有
个
13.把抛物线y=ax+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x-3x+5,则a+b+c=__________
14.从地面垂直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的函数关系式是h=9.8t-4.9t2,那么小球运动中的最大高度为
米.
15.如图所示,抛物线y=ax2+bx+c()与轴的两个交点分别为A(-1,0)和B(2,0),当y<0
时,x的取值范围是
.
16.出售某种文具盒,若每个获利x元,一天可售出(6-x)个,则当
元时,一天出售该种文具盒的总利润y最大.
17.若梯形的下底长为x,上底长为下底长的,高为y,面积为60,则y与x的函数关系是____________.(不考虑的取值范围)
18.如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数
(x>0)的图象上,则点E的坐标是___
19.如图,函数y=x与的图象交于A、B两点,过点A作AC垂直于y轴,垂足为C,则的面积为
.
20.如图,为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,-1<x<3.其中,正确的说法有
.(请写出所有正确说法的序号)
三、解答题(每题10分,共60分)
21.下表是佳佳往妹妹家打长途电话的几次收费记载:
时间/分
1
2
3
4
5
6
7
电话费/元
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)你能帮佳佳预测一下,如果她打电话用时间是10分钟,则需付多少电话费?
22.已知关于x的一元二次方程2x2+4x+k-1=0有实数根,为正整数
(1)求的值;
(2)当此方程有两个非零的整数根时,将关于的二次函数y=2x2+4x+k-1的图象向下平移8个单位,求平移后的图象的解析式;
23.为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(分钟)成正比例;药物释放完毕后,与成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,与之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
24.如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数
(k为常数,)的图象相交于点
A(1,3).
(1)求这两个函数的解析式及其图象的另一交点的坐标;
(2)观察图象,写出使函数值y1≥y2的自变量的取值范围.
四、拓广探索(10分)
25.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
选做题
26.如图,已知抛物线与轴的两个交点为,与y轴交于点.
(1)求三点的坐标;
(2)求证:是直角三角形;
(3)若坐标平面内的点,使得以点和三点为顶点的四边形是平行四边形,求点的坐标.(直接写出点的坐标,不必写求解过程)
参考答案:
一、1.A;2.C;3、D;4.C;5、A;6、D;7、C;8、C;9、C;10、D;
二、11.;12、2;13、11;14、4.9;15、或;
16、3;17、;18、(,);19、4;20、①②④;
三、21.(1)通话时间与电话费;其中通话时间是自变量,电话费是因变量;(2)6元.
22、解:(1)由题意得,.∴.∵为正整数,∴.
(2)当时,方程有一个根为零;
当时,方程无整数根;
当时,方程有两个非零的整数根.
综上所述,和不合题意,舍去;符合题意.
当时,二次函数为,把它的图象向下平移8个单位得到的图象的解析式为.
23、解:(1)药物释放过程中与的函数关系式为(0≤≤12),药物释放完毕后与的函数关系式为(≥12)
(2)
解之,得
(分钟)(小时),
答:
从药物释放开始,至少需要经过4小时后,学生才能进入教室.
24、解:(1)由题意,得,解得,所以一次函数的解析式为.
由题意,得,解得,所以反比例函数的解析式为.
由题意,得,解得.当时,,所以交点.)
(2)由图象可知,当或时,函数值.
25、解:(1)根据题意得解得.
所求一次函数的表达式为.
(2),
抛物线的开口向下,当时,随的增大而增大,而,
当时,.
当销售单价定为87元时,商场可获得最大利润,最大利润是891元.
(3)由,得,
整理得,,解得,.
由图象可知,要使该商场获得利润不低于500元,销售单价应在70元到110元之间,而,所以,销售单价的范围是.
26、(1)解:令,得,得点.
令,得,解得,
∴.
(2)法一:证明:因为,
,
∴,
∴是直角三角形.
法二:因为,∴,
∴,又,∴.
∴,∴,
∴,即是直角三角形.
(3),,.
第1题图
第4题图
x
y
O
A
B
第7题图
1
O
x
y
(第6题图)
y
x
O
y
x
O
B.
C.
y
x
O
A.
y
x
O
D.
第9题图
O
A
C
B
x
y
第20题图
第19题图
第18题图
第15题图
O
9
(毫克)
12
(分钟)
第23题图
y
x
B
1
2
3
3
1
2
A(1,3)
第24题图
O
A
B
x
y
C
第26题图
O
A
B
x
y
C
26题图
N
M2
M1
M3
