人教版九年级数学上册23.1 图形的旋转 课件(第二课时 共20张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.1 图形的旋转 课件(第二课时 共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 12:21:55 | ||
图片预览





文档简介
(共20张PPT)
23.1 图形的旋转(第2课时)
九年级 上册
学习目标:
1.理解选择不同的旋转中心、不同的旋转角度对某
一图案作旋转,会出现不同的效果,掌握根据需
要用旋转的知识设计出美丽的图案;
2.复习图形旋转的基本性质,着重强调旋转中心和
旋转角,然后应用已学的知识作图,设计出美丽
的图案.
学习重点:
根据需要设计美丽图案.
课件说明
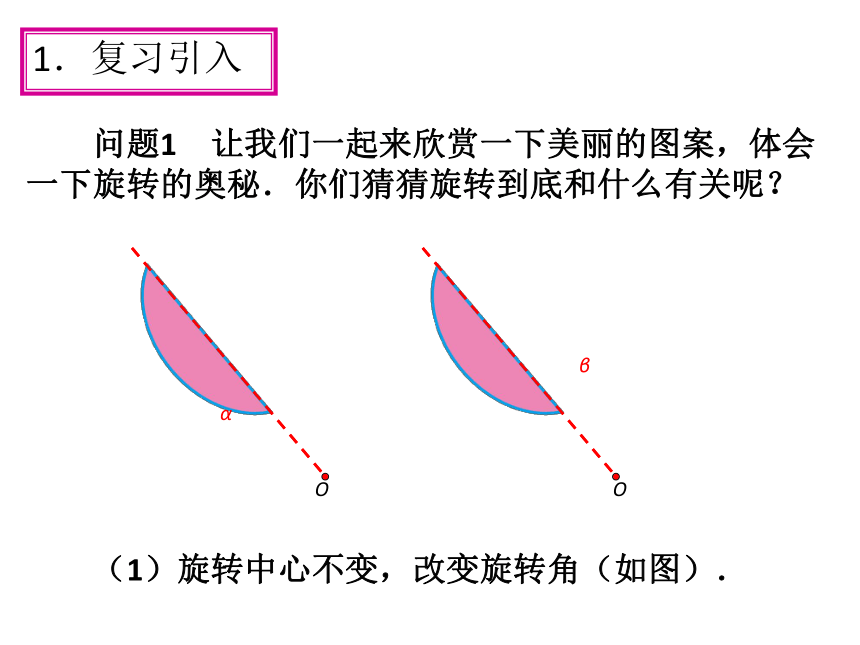
(1)旋转中心不变,改变旋转角(如图).
问题1 让我们一起来欣赏一下美丽的图案,体会
一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
1.复习引入
O
O
β
α
1.复习引入
O1
α
O2
α
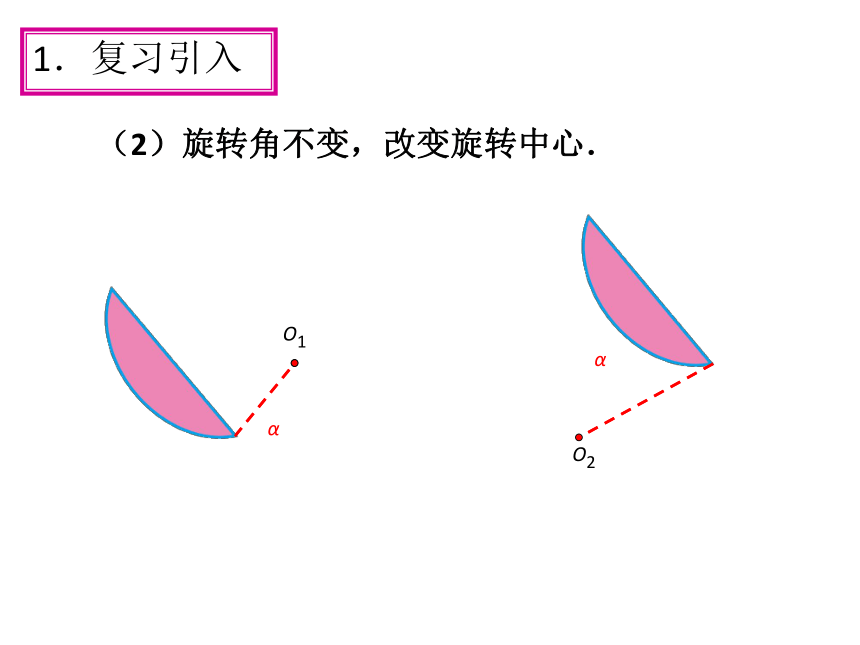
(2)旋转角不变,改变旋转中心.
1.复习引入
(3)美丽的图案是这样形成的.
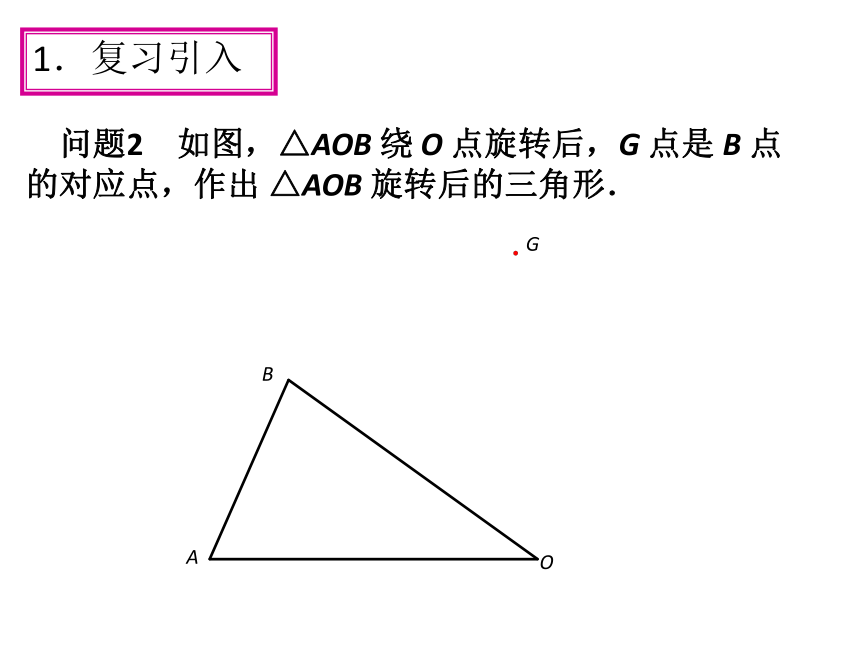
问题2 如图,△AOB
绕
O
点旋转后,G
点是
B
点
的对应点,作出
△AOB
旋转后的三角形.
1.复习引入
O
例1 如下图是某一种花的花瓣和中心,现以
O
为
旋转中心画出分别旋转
45°,
90°
,135°
,180°
,
225°,
270°,
315°的这种花的图形.
2.探究新知
2.探究新知
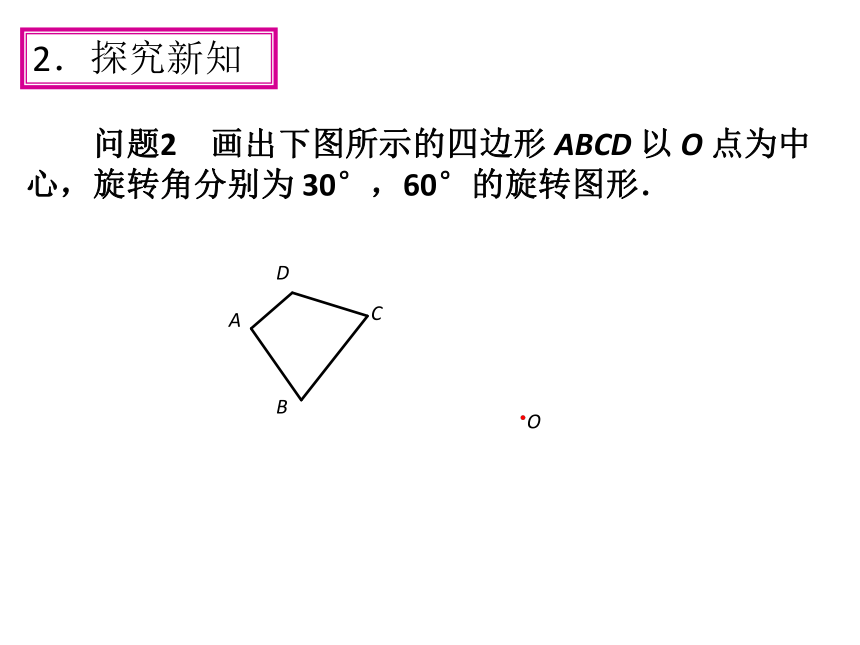
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
2.探究新知
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
顺时针旋转
60°
顺时针旋转
30°
2.探究新知
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
逆时针旋转
60°
逆时针旋转
30°
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
2.探究新知
2.探究新知
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
绕
O1
顺时针旋转
30°
绕
O2
顺时针旋转
30°
2.探究新知
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
绕
O1
逆时针旋转
30°
绕
O2
逆时针旋转
30°
把一个三角形进行旋转:
(1)选择不同的旋转中心,不同的旋转角,看看旋
转的效果;
3.巩固练习
(2)改变三角形的形状,看看旋转的效果.
3.巩固练习
练习:将图2沿MN翻折180°,再旋转180°,所得图形是(
)
旋转识图
探究三:拓展应用
活动1
重点、难点知识
★▲
例1.将图1绕O点顺时针旋转90°,得到图形是(
)
D
B
【思路点拨】抓住翻折的性质和旋转的三要素是解题的关键。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
(1)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)。
①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
①分别将点A、B、C向上平移1个单位,再向右平移5个单位,然后顺次连接;
②根据网格结构
找出点A、B、C
以点O为旋转中心
顺时针旋转90°后
的对应点,然后
顺次连接即可。
【解题过程】
【思路点拨】抓住平移和旋转的要素。
A
B
C
D
E
F
4.如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心。
旋转中心在对应点连线的垂直平分线上。
O
23.1
图的旋转
23.1 图形的旋转(第2课时)
九年级 上册
学习目标:
1.理解选择不同的旋转中心、不同的旋转角度对某
一图案作旋转,会出现不同的效果,掌握根据需
要用旋转的知识设计出美丽的图案;
2.复习图形旋转的基本性质,着重强调旋转中心和
旋转角,然后应用已学的知识作图,设计出美丽
的图案.
学习重点:
根据需要设计美丽图案.
课件说明
(1)旋转中心不变,改变旋转角(如图).
问题1 让我们一起来欣赏一下美丽的图案,体会
一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
1.复习引入
O
O
β
α
1.复习引入
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
1.复习引入
(3)美丽的图案是这样形成的.
问题2 如图,△AOB
绕
O
点旋转后,G
点是
B
点
的对应点,作出
△AOB
旋转后的三角形.
1.复习引入
O
例1 如下图是某一种花的花瓣和中心,现以
O
为
旋转中心画出分别旋转
45°,
90°
,135°
,180°
,
225°,
270°,
315°的这种花的图形.
2.探究新知
2.探究新知
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
2.探究新知
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
顺时针旋转
60°
顺时针旋转
30°
2.探究新知
问题2 画出下图所示的四边形
ABCD
以
O
点为中
心,旋转角分别为
30°,60°的旋转图形.
逆时针旋转
60°
逆时针旋转
30°
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
2.探究新知
2.探究新知
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
绕
O1
顺时针旋转
30°
绕
O2
顺时针旋转
30°
2.探究新知
问题3 画出下图所示的四边形
ABCD
分别以
O1,
O2
为中心,旋转角都为
30°的旋转图形.
绕
O1
逆时针旋转
30°
绕
O2
逆时针旋转
30°
把一个三角形进行旋转:
(1)选择不同的旋转中心,不同的旋转角,看看旋
转的效果;
3.巩固练习
(2)改变三角形的形状,看看旋转的效果.
3.巩固练习
练习:将图2沿MN翻折180°,再旋转180°,所得图形是(
)
旋转识图
探究三:拓展应用
活动1
重点、难点知识
★▲
例1.将图1绕O点顺时针旋转90°,得到图形是(
)
D
B
【思路点拨】抓住翻折的性质和旋转的三要素是解题的关键。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
(1)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)。
①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O。
旋转作图
探究三:拓展应用
活动2
重点、难点知识
★▲
①分别将点A、B、C向上平移1个单位,再向右平移5个单位,然后顺次连接;
②根据网格结构
找出点A、B、C
以点O为旋转中心
顺时针旋转90°后
的对应点,然后
顺次连接即可。
【解题过程】
【思路点拨】抓住平移和旋转的要素。
A
B
C
D
E
F
4.如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心。
旋转中心在对应点连线的垂直平分线上。
O
23.1
图的旋转
同课章节目录
