人教版数学七年级上册:2.1整式 课件(39张PPT)
文档属性
| 名称 | 人教版数学七年级上册:2.1整式 课件(39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
整式
观察下列代数式
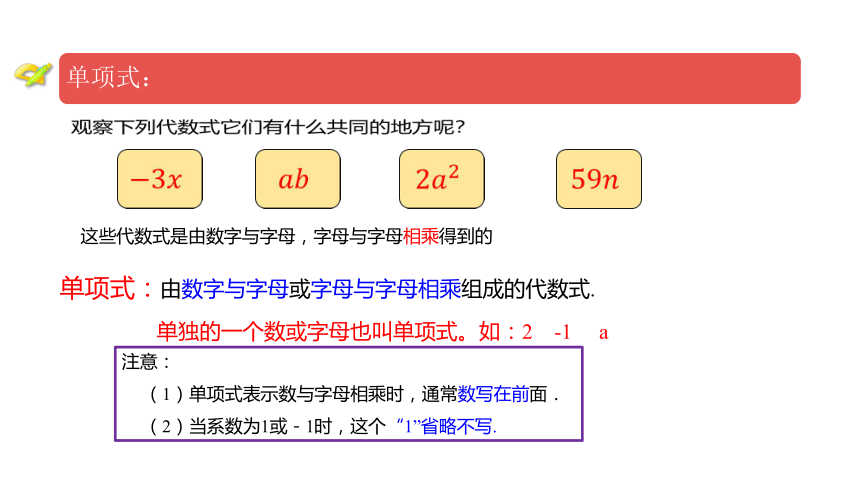
单项式:
这些代数式是由数字与字母,字母与字母相乘得到的
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式。如:2
-1
a
单项式:
观察下列代数式
注意:
(1)单项式表示数与字母相乘时,通常数写在前面.
(2)当系数为1或-1时,这个“1”省略不写.
单项式:
4
【例1】判断:下列各式是不是单项式
-ab
你觉得单项式中对字
母有什么要求?
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式.
研究单项式:
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
(注意:要连同数字前面的符号)
次数:先确定有几个字母,再
确定每个字母的指数,
最后相加
单项式:
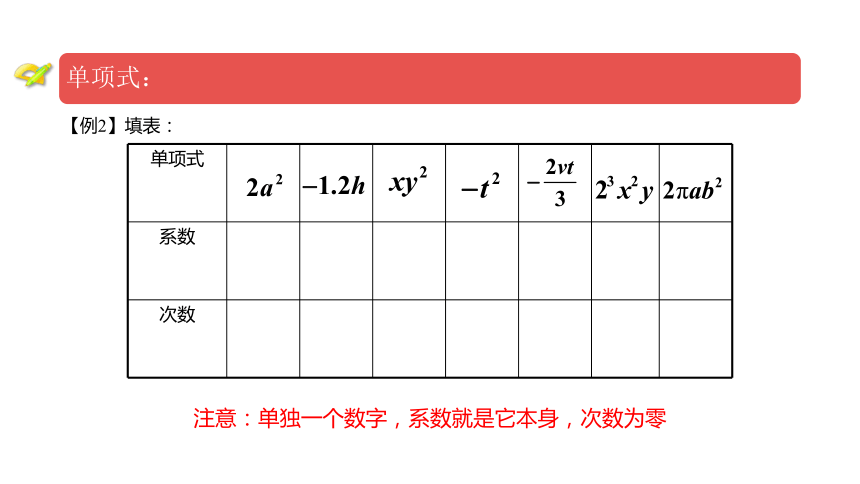
【例2】填表:
单项式
系数
次数
注意:单独一个数字,系数就是它本身,次数为零
单项式:
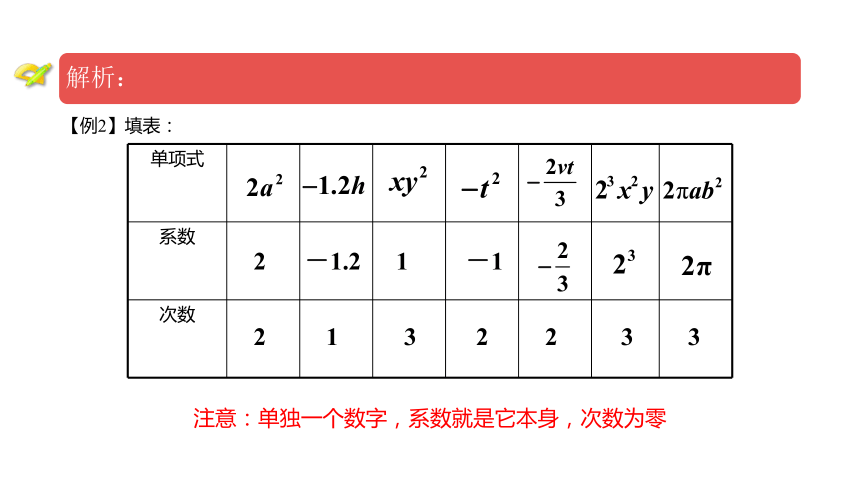
【例2】填表:
单项式
系数
次数
2
2
-1.2
1
1
3
-1
2
2
3
3
注意:单独一个数字,系数就是它本身,次数为零
解析:
观察代数式有什么共同点?
多项式:
可以看做是由数字与字母,字母与字母的积的和差得到的。
多项式:由几个单项式相加组成的代数式
【例3】判断:下列各式是不是多项式.
多项式:
观察代数式有什么共同点?
研究多项式:
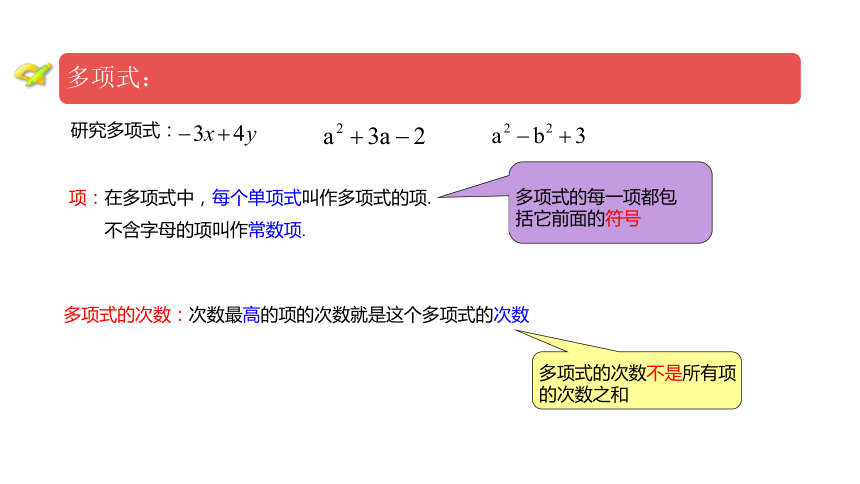
项:在多项式中,每个单项式叫作多项式的项.
不含字母的项叫作常数项.
多项式的次数:次数最高的项的次数就是这个多项式的次数
多项式的每一项都包括它前面的符号
多项式的次数不是所有项的次数之和
多项式:
单项式和多项式统称为整式.
多项式:
【例4】说出下列各多项式的项,找出每一项的系数,每一项的次数,是一个几次几项式.
【例5】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
整式:
多项式:
单项式:
多项式:
【例5】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
整式:
多项式:
单项式:
解析:
【练5】1.关于单项式,下列结论中正确的是(
)
A.系数是-2,次数是4
B.系数是-2,次数是5
C.系数是-2,次数是8
D.系数是-8,次数是5
2.下列结论正确的是(
)
A.xyz的系数为0
B.3x2-x+1
中一次项系数为-1
C.a2b3c的次数为5
D.a2-33是一个三次二项式
3.下列关于多项式-2m2-1-4m的说法中,正确的是(
)
A.常数项是1
B.是二次三项式
C.一次项是4m
D.最高次项是-2
多项式:
4.若单项式的次数与单项式的次数相同,则m等于
.
5.
(k-2)x2-5x+9是关于x的一次多项式,则
k=______。
6.m为
时,多项式
是五次二项式.
7.写出满足下列三个条件的所有单项式
(1)系数为-5
(2)都含有字母ab
(3)次数为4次
多项式:
15
4.若单项式的次数与单项式的次数相同,则m等于
2
.
5.
(k-2)x2-5x+9是关于x的一次多项式,则
k=___2___。
6.m为
2
时,多项式
是五次二项式.
7.写出满足下列三个条件的所有单项式
(1)系数为-5
(2)都含有字母ab
(3)次数为4次
-5
-5
-5
解析:
16
把具有相同特征的事物归为一类
将下列整式进行分类,并说说你为什么这么分类?
8a
-7a2b
2a2b
-3xy
5a
6xy
同类项:
多项式中,所含字母相同,并且相同字母的指数也相同的项,称为同类项.
所有的常数项是同类项.
【例6】判断下列各组是不是同类项:
(1)x和3x
(2)4a2b与ab2
(3)-3pq与5qp
(4)bc与ac
(5)6a2与a3
(6)8与3
同类项:
小贴士:
(1)同类项特点:
①字母相同;②相同字母的指数也相同;
(2)同类项的前提是单项式;
(3)同类项与系数与字母顺序无关。
a2b
+
4a2b
=
(
__
+
__
)a2b
=
__
a2b
1
4
5
把多项式中的同类项合并成一项,叫做合并同类项.
1
合并同类项的法则:
1、同类项的系数相加,所得结果作为系数.
2、字母和字母的指数不变.
同类项:
合并同类项步骤:
(一分)
(二移)
(三合并)
移时要连同项的符号
合并同类项:
=
=
【练6-1】下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=3a
合并同类项:
【练6-2】合并同类项:
(1)2ab+3ab-6ab.
(2)6xy-10x2-5yx+7x2+5x.
(3)3x-8x-xy2-x2y+xy2.
(4)5a2+2ab-4a2-4ab.
合并同类项:
23
【练6-2】合并同类项:
(1)2ab+3ab-6ab.
(2)6xy-10x2-5yx+7x2+5x.
答案:原式=(2+3-6)ab=-ab.
答案:原式=xy-3x2+5x.
(3)3x-8x-xy2-x2y+xy2.
(4)5a2+2ab-4a2-4ab.
答案:原式=-5x-x2y.
答案:原式=a2-2ab.
解析:
24
【练6-3】1.已知单项式3x3ym与-xn-1y2是同类项,则m=
,n=
.
2.若单项式ax2yn+1与-axmy4的和仍是单项式,则m-2n=_______.
3.如果关于x的多项式的值与x的值无关,求的值.
合并同类项:
【练6-3】1.已知单项式3x3ym与-xn-1y2是同类项,则m=
,n=
.
2.若单项式ax2yn+1与-axmy4的和仍是单项式,则m-2n=___-4____.
4
2
zxxk
学科网
解析:
3.如果关于x的多项式的值与x的值无关,求的值.
解:
因为该多项式的值与x无关,
所以,解得
所以
【例7】先合并同类项,再求值:
(1)4xy-3x2-3xy-2y+2x2,其中x=-1,y=1.
(2)5a3-3b2-5a3+4b2+2ab,其中a=-1,b=
.
合并同类项:
27
【例7】先合并同类项,再求值:
(1)4xy-3x2-3xy-2y+2x2,其中x=-1,y=1.
(2)5a3-3b2-5a3+4b2+2ab,其中a=-1,b=
.
解析:
28
【练7】先化简,再求值:
其中a=-2
,b=3.
,其中
合并同类项:
提示:可以将和先分别看作一个整体哦
【练7】先化简,再求值:
其中a=-2
,b=3.
,其中
解析:
提示:可以将和先分别看作一个整体哦
解.
解
当堂检测:
31
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则(
)
A.m=-5,n=-1
B.m=5,n=1
C.m=-5,n=1
D.m=5,n=-1
3.x|m|-(m-4)x+7是关于x的四次三项式,则m的值是(
)
A.4
B.-2
C.-4
D.4或-4
解析:
32
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则(
C
)
A.m=-5,n=-1
B.m=5,n=1
C.m=-5,n=1
D.m=5,n=-1
3.x|m|-(m-4)x+7是关于x的四次三项式,则m的值是(
C
)
A.4
B.-2
C.-4
D.4或-4
C
4.把下列代数式分别填在相应的括号内.
①单项式:
②多项式:
③二次二项式:
当堂检测:
33
4.把下列代数式分别填在相应的括号内.
①单项式:
②多项式:
③二次二项式:
解析:
34
5.指出下列多项式的项和次数,并说明它们是几次几项式.
(1)x4-x2-1.
(2)-3a2-3b2+1.
(3)-2x6+x5y2-x2y5-2xy3+1.
当堂检测:
35
5.指出下列多项式的项和次数,并说明它们是几次几项式.
(1)x4-x2-1.
(2)-3a2-3b2+1.
(3)-2x6+x5y2-x2y5-2xy3+1.
解:(1)x4-x2-1的项是x4,-x2,-1,次数是4,是四次三项式.
(2)-3a2-3b2+1的项是-3a2,-3b2,1,次数是2,是二次三项式.
(3)-2x6+x5y2-x2y5-2xy3+1的项是-2x6,x5y2,-x2y5,-2xy3,1,次数是7,
是七次五项式.
解析:
36
6.先合并同类项,再求值.
(1)x3-2x2+x3+3x2+5x-4x+7.其中x=0.1.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.其中x=1,y=.
当堂检测:
37
6.先合并同类项,再求值.
(1)x3-2x2+x3+3x2+5x-4x+7.其中x=0.1.
解:原式=x3+x2+x+7,把x=0.1代入,得原式=7.111.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.其中x=1,y=.
解析:
38
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
多项式:由几个单项式相加组成的代数式
项:在多项式中,每个单项式叫作多项式的项
多项式的次数:次数最高的项的次数就是这个多项式的次数
整式:单项式和多项式统称为整式。
当堂总结
39
1.字母相同
2.相同字母指数相同
同类项
合并同类项
1.找同类项
2.合并同类项
系数相加
字母及字母指数不变
整式
观察下列代数式
单项式:
这些代数式是由数字与字母,字母与字母相乘得到的
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式。如:2
-1
a
单项式:
观察下列代数式
注意:
(1)单项式表示数与字母相乘时,通常数写在前面.
(2)当系数为1或-1时,这个“1”省略不写.
单项式:
4
【例1】判断:下列各式是不是单项式
-ab
你觉得单项式中对字
母有什么要求?
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式.
研究单项式:
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
(注意:要连同数字前面的符号)
次数:先确定有几个字母,再
确定每个字母的指数,
最后相加
单项式:
【例2】填表:
单项式
系数
次数
注意:单独一个数字,系数就是它本身,次数为零
单项式:
【例2】填表:
单项式
系数
次数
2
2
-1.2
1
1
3
-1
2
2
3
3
注意:单独一个数字,系数就是它本身,次数为零
解析:
观察代数式有什么共同点?
多项式:
可以看做是由数字与字母,字母与字母的积的和差得到的。
多项式:由几个单项式相加组成的代数式
【例3】判断:下列各式是不是多项式.
多项式:
观察代数式有什么共同点?
研究多项式:
项:在多项式中,每个单项式叫作多项式的项.
不含字母的项叫作常数项.
多项式的次数:次数最高的项的次数就是这个多项式的次数
多项式的每一项都包括它前面的符号
多项式的次数不是所有项的次数之和
多项式:
单项式和多项式统称为整式.
多项式:
【例4】说出下列各多项式的项,找出每一项的系数,每一项的次数,是一个几次几项式.
【例5】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
整式:
多项式:
单项式:
多项式:
【例5】下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
整式:
多项式:
单项式:
解析:
【练5】1.关于单项式,下列结论中正确的是(
)
A.系数是-2,次数是4
B.系数是-2,次数是5
C.系数是-2,次数是8
D.系数是-8,次数是5
2.下列结论正确的是(
)
A.xyz的系数为0
B.3x2-x+1
中一次项系数为-1
C.a2b3c的次数为5
D.a2-33是一个三次二项式
3.下列关于多项式-2m2-1-4m的说法中,正确的是(
)
A.常数项是1
B.是二次三项式
C.一次项是4m
D.最高次项是-2
多项式:
4.若单项式的次数与单项式的次数相同,则m等于
.
5.
(k-2)x2-5x+9是关于x的一次多项式,则
k=______。
6.m为
时,多项式
是五次二项式.
7.写出满足下列三个条件的所有单项式
(1)系数为-5
(2)都含有字母ab
(3)次数为4次
多项式:
15
4.若单项式的次数与单项式的次数相同,则m等于
2
.
5.
(k-2)x2-5x+9是关于x的一次多项式,则
k=___2___。
6.m为
2
时,多项式
是五次二项式.
7.写出满足下列三个条件的所有单项式
(1)系数为-5
(2)都含有字母ab
(3)次数为4次
-5
-5
-5
解析:
16
把具有相同特征的事物归为一类
将下列整式进行分类,并说说你为什么这么分类?
8a
-7a2b
2a2b
-3xy
5a
6xy
同类项:
多项式中,所含字母相同,并且相同字母的指数也相同的项,称为同类项.
所有的常数项是同类项.
【例6】判断下列各组是不是同类项:
(1)x和3x
(2)4a2b与ab2
(3)-3pq与5qp
(4)bc与ac
(5)6a2与a3
(6)8与3
同类项:
小贴士:
(1)同类项特点:
①字母相同;②相同字母的指数也相同;
(2)同类项的前提是单项式;
(3)同类项与系数与字母顺序无关。
a2b
+
4a2b
=
(
__
+
__
)a2b
=
__
a2b
1
4
5
把多项式中的同类项合并成一项,叫做合并同类项.
1
合并同类项的法则:
1、同类项的系数相加,所得结果作为系数.
2、字母和字母的指数不变.
同类项:
合并同类项步骤:
(一分)
(二移)
(三合并)
移时要连同项的符号
合并同类项:
=
=
【练6-1】下列各题合并同类项的结果对不对?不对的,指出错在哪里.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=3a
合并同类项:
【练6-2】合并同类项:
(1)2ab+3ab-6ab.
(2)6xy-10x2-5yx+7x2+5x.
(3)3x-8x-xy2-x2y+xy2.
(4)5a2+2ab-4a2-4ab.
合并同类项:
23
【练6-2】合并同类项:
(1)2ab+3ab-6ab.
(2)6xy-10x2-5yx+7x2+5x.
答案:原式=(2+3-6)ab=-ab.
答案:原式=xy-3x2+5x.
(3)3x-8x-xy2-x2y+xy2.
(4)5a2+2ab-4a2-4ab.
答案:原式=-5x-x2y.
答案:原式=a2-2ab.
解析:
24
【练6-3】1.已知单项式3x3ym与-xn-1y2是同类项,则m=
,n=
.
2.若单项式ax2yn+1与-axmy4的和仍是单项式,则m-2n=_______.
3.如果关于x的多项式的值与x的值无关,求的值.
合并同类项:
【练6-3】1.已知单项式3x3ym与-xn-1y2是同类项,则m=
,n=
.
2.若单项式ax2yn+1与-axmy4的和仍是单项式,则m-2n=___-4____.
4
2
zxxk
学科网
解析:
3.如果关于x的多项式的值与x的值无关,求的值.
解:
因为该多项式的值与x无关,
所以,解得
所以
【例7】先合并同类项,再求值:
(1)4xy-3x2-3xy-2y+2x2,其中x=-1,y=1.
(2)5a3-3b2-5a3+4b2+2ab,其中a=-1,b=
.
合并同类项:
27
【例7】先合并同类项,再求值:
(1)4xy-3x2-3xy-2y+2x2,其中x=-1,y=1.
(2)5a3-3b2-5a3+4b2+2ab,其中a=-1,b=
.
解析:
28
【练7】先化简,再求值:
其中a=-2
,b=3.
,其中
合并同类项:
提示:可以将和先分别看作一个整体哦
【练7】先化简,再求值:
其中a=-2
,b=3.
,其中
解析:
提示:可以将和先分别看作一个整体哦
解.
解
当堂检测:
31
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则(
)
A.m=-5,n=-1
B.m=5,n=1
C.m=-5,n=1
D.m=5,n=-1
3.x|m|-(m-4)x+7是关于x的四次三项式,则m的值是(
)
A.4
B.-2
C.-4
D.4或-4
解析:
32
2.已知关于x的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3和x2,则(
C
)
A.m=-5,n=-1
B.m=5,n=1
C.m=-5,n=1
D.m=5,n=-1
3.x|m|-(m-4)x+7是关于x的四次三项式,则m的值是(
C
)
A.4
B.-2
C.-4
D.4或-4
C
4.把下列代数式分别填在相应的括号内.
①单项式:
②多项式:
③二次二项式:
当堂检测:
33
4.把下列代数式分别填在相应的括号内.
①单项式:
②多项式:
③二次二项式:
解析:
34
5.指出下列多项式的项和次数,并说明它们是几次几项式.
(1)x4-x2-1.
(2)-3a2-3b2+1.
(3)-2x6+x5y2-x2y5-2xy3+1.
当堂检测:
35
5.指出下列多项式的项和次数,并说明它们是几次几项式.
(1)x4-x2-1.
(2)-3a2-3b2+1.
(3)-2x6+x5y2-x2y5-2xy3+1.
解:(1)x4-x2-1的项是x4,-x2,-1,次数是4,是四次三项式.
(2)-3a2-3b2+1的项是-3a2,-3b2,1,次数是2,是二次三项式.
(3)-2x6+x5y2-x2y5-2xy3+1的项是-2x6,x5y2,-x2y5,-2xy3,1,次数是7,
是七次五项式.
解析:
36
6.先合并同类项,再求值.
(1)x3-2x2+x3+3x2+5x-4x+7.其中x=0.1.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.其中x=1,y=.
当堂检测:
37
6.先合并同类项,再求值.
(1)x3-2x2+x3+3x2+5x-4x+7.其中x=0.1.
解:原式=x3+x2+x+7,把x=0.1代入,得原式=7.111.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.其中x=1,y=.
解析:
38
单项式:由数字与字母或字母与字母相乘组成的代数式.
单独的一个数或字母也叫单项式
系数:单项式中的数字因数
次数:单项式中所有字母的指数和
多项式:由几个单项式相加组成的代数式
项:在多项式中,每个单项式叫作多项式的项
多项式的次数:次数最高的项的次数就是这个多项式的次数
整式:单项式和多项式统称为整式。
当堂总结
39
1.字母相同
2.相同字母指数相同
同类项
合并同类项
1.找同类项
2.合并同类项
系数相加
字母及字母指数不变
