人教版 七年级数学上册讲义:4.3 角的概念与大小比较 (含解析)
文档属性
| 名称 | 人教版 七年级数学上册讲义:4.3 角的概念与大小比较 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 07:09:42 | ||
图片预览




文档简介
69532585725
第12讲 角的概念与大小比较
0329565
知识定位
讲解用时:5分钟
A、适用范围:人教版初一,基础一般;
B、知识点概述:本讲义主要用于人教版初一新课,主要学习角的概念与大小比较,掌握角的概念及角的表示方法,并能进行角度的互换;能借助三角尺画一些特殊角,掌握角大小的比较方法;会利用角平分线的意义进行有关表示或计算;掌握角的和、差、倍、分关系,并会进行有关计算.
0137160
知识梳理
讲解用时:15分钟
381033020角的定义及其表示方法
角的定义及其表示方法
-57151905(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
角也可以看作是由一条射线绕着它的端点旋转而形成的图形.当终边和始边成一条直线时,形成等角;当终边和始边重合时,形成周角.
(2)角的表示方法:
有四种表示角的方法:
①用一个阿拉伯数字表示单独的一个角,在角内用一段弧标注;
②用一个大写英文字母表示单独的一个角,当角的顶点处有两个或两个以上的角时,不能用这种方法表示角;
③用一个小写希腊字母表示单独的一个角;
④用三个大写英文字母表示任意一个角,这时表示顶点的字母一定要写在中间.
角的理解 (1)角的大小与边的长短无关,只与构成角的两条射线张开的幅度大小有关,角可以度量,可以比较大小,可以进行运算;(2)如果没有特别说明,所说的角都是指小于平角的角.
(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
角也可以看作是由一条射线绕着它的端点旋转而形成的图形.当终边和始边成一条直线时,形成等角;当终边和始边重合时,形成周角.
(2)角的表示方法:
有四种表示角的方法:
①用一个阿拉伯数字表示单独的一个角,在角内用一段弧标注;
②用一个大写英文字母表示单独的一个角,当角的顶点处有两个或两个以上的角时,不能用这种方法表示角;
③用一个小写希腊字母表示单独的一个角;
④用三个大写英文字母表示任意一个角,这时表示顶点的字母一定要写在中间.
角的理解 (1)角的大小与边的长短无关,只与构成角的两条射线张开的幅度大小有关,角可以度量,可以比较大小,可以进行运算;(2)如果没有特别说明,所说的角都是指小于平角的角.
3810143510角的度量与换算
角的度量与换算
133351187451.角度制:以度、分、秒为单位的角的度量制,叫做角度制.
2.角度的换算:
角的度量单位是度、分、秒,把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份就是1分的角,记作1′;把1分的角60等分,每一份就是1秒的角,记作1″.
角度的换算
(1)度、分、秒的换算是60进制,与时间中的时、分、秒的换算相同;
(2)角的度数的换算有两种方法:
①由度化成度、分、秒的形式(即从高位向低位化),用乘法,1°=60′,
1′=60″;
②由度、分、秒化成度的形式(即从低位向高位化),1″=′,1′=°,用除法.
注意:度及度、分、秒之间的转化必须逐级进行转化,“越级”转化容易出错.
1.角度制:以度、分、秒为单位的角的度量制,叫做角度制.
2.角度的换算:
角的度量单位是度、分、秒,把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份就是1分的角,记作1′;把1分的角60等分,每一份就是1秒的角,记作1″.
角度的换算
(1)度、分、秒的换算是60进制,与时间中的时、分、秒的换算相同;
(2)角的度数的换算有两种方法:
①由度化成度、分、秒的形式(即从高位向低位化),用乘法,1°=60′,
1′=60″;
②由度、分、秒化成度的形式(即从低位向高位化),1″=′,1′=°,用除法.
注意:度及度、分、秒之间的转化必须逐级进行转化,“越级”转化容易出错.
-1104902520951.角的比较:
(1)度量法:用量角器量出角的度数,然后按照度数比较角的大小,度数大的角大,度数小的角小;反之,角大度数大,角小度数小.
(2)叠合法:把两个角的顶点和一边分别重合,另一边放在重合边的同旁,通过另一边的位置关系比较大小.
技巧 角的比较 ①在度量法中,注意三点:对中、重合、度数;②在叠合法中,要注意顶点重合,一边重合,另一边落在重合这边的同侧.
1.角的比较:
(1)度量法:用量角器量出角的度数,然后按照度数比较角的大小,度数大的角大,度数小的角小;反之,角大度数大,角小度数小.
(2)叠合法:把两个角的顶点和一边分别重合,另一边放在重合边的同旁,通过另一边的位置关系比较大小.
技巧 角的比较 ①在度量法中,注意三点:对中、重合、度数;②在叠合法中,要注意顶点重合,一边重合,另一边落在重合这边的同侧.
-34290116205角的比较与运算
角的比较与运算
-1962151225552.角的和差:
角的和、差有两种意义,几何意义和代数意义.几何意义对于今后读图形语言有很大帮助,代数意义是今后角的运算的基础.
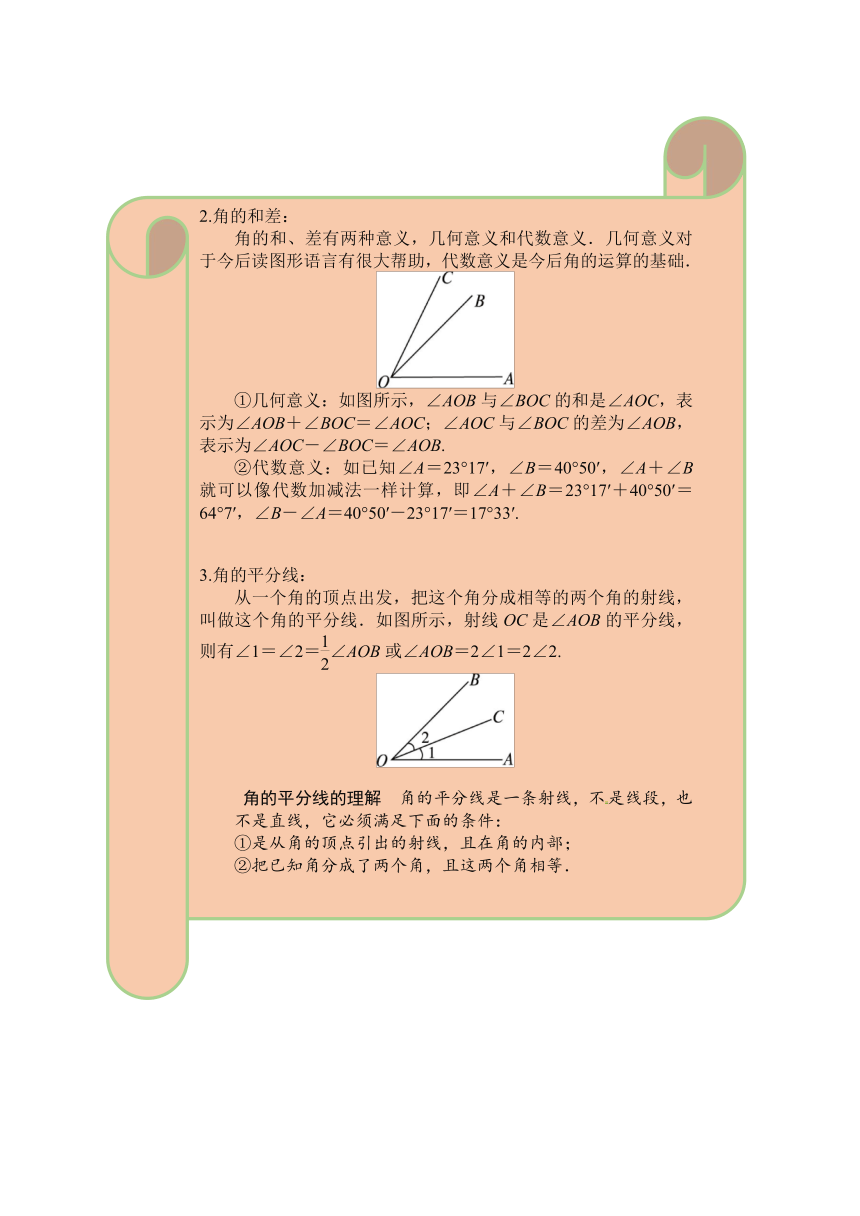
①几何意义:如图所示,∠AOB与∠BOC的和是∠AOC,表示为∠AOB+∠BOC=∠AOC;∠AOC与∠BOC的差为∠AOB,表示为∠AOC-∠BOC=∠AOB.
②代数意义:如已知∠A=23°17′,∠B=40°50′,∠A+∠B就可以像代数加减法一样计算,即∠A+∠B=23°17′+40°50′=64°7′,∠B-∠A=40°50′-23°17′=17°33′.
3.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.如图所示,射线OC是∠AOB的平分线,则有∠1=∠2=∠AOB或∠AOB=2∠1=2∠2.
角的平分线的理解 角的平分线是一条射线,不是线段,也不是直线,它必须满足下面的条件:
①是从角的顶点引出的射线,且在角的内部;
②把已知角分成了两个角,且这两个角相等.
2.角的和差:
角的和、差有两种意义,几何意义和代数意义.几何意义对于今后读图形语言有很大帮助,代数意义是今后角的运算的基础.
①几何意义:如图所示,∠AOB与∠BOC的和是∠AOC,表示为∠AOB+∠BOC=∠AOC;∠AOC与∠BOC的差为∠AOB,表示为∠AOC-∠BOC=∠AOB.
②代数意义:如已知∠A=23°17′,∠B=40°50′,∠A+∠B就可以像代数加减法一样计算,即∠A+∠B=23°17′+40°50′=64°7′,∠B-∠A=40°50′-23°17′=17°33′.
3.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.如图所示,射线OC是∠AOB的平分线,则有∠1=∠2=∠AOB或∠AOB=2∠1=2∠2.
角的平分线的理解 角的平分线是一条射线,不是线段,也不是直线,它必须满足下面的条件:
①是从角的顶点引出的射线,且在角的内部;
②把已知角分成了两个角,且这两个角相等.
-8572547625 课堂精讲精练
【例题1】
(1)在∠AOB内部画1条射线OC,则图1中有 个不同的角;
(2)在∠AOB内部画2条射线OC,OD,则图2中有 个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有 个不同的角;
【答案】(1)3;(2)6;(3)10.
【解析】
解:(1)在∠AOB内部画1条射线OC,则图中有3个不同的角,
故答案为:3.
(2)在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,
故答案为:6.
(3)在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,
故答案为:10.
讲解用时:5分钟
解题思路:根据角的概念,结合图形,即可数出角的个数.
教学建议:考查了角的有关概念的应用
难度: 3 适应场景:当堂例题 例题来源:无
【练习1.1】
如图所示,下列表示角的方法错误的是( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
【答案】D.
【解析】
解:A、∠1与∠AOB表示同一个角,正确,故本选项错误;
B、∠β表示的是∠BOC,正确,故本选项错误;
C、图中共有三个角:∠AOB,∠AOC,∠BOC,正确,故本选项错误;
D、∠AOC不能用∠O表示,错误,故本选项正确;
故选:D.
讲解用时:3分钟
解题思路:根据角的表示方法表示各个角,再判断即可.
教学建议:本题考查了对角的表示方法的应用,主要检查学生能否正确表示角.
难度: 3 适应场景:当堂练习 例题来源:无
【例题2】
(1)将70.23°用度、分、秒表示;
(2)将26°48′36″用度表示.
【答案】(1)70°13′48″;(2)26.81°.
【解析】
解:(1)将0.23°化为分,可得0.23×60′=13.8′,再把0.8′化为秒,得0.8×60″=48″.
所以70.23°=70°13′48″.
(2)把36″化成分,36″=false×36=0.6′,48′+0.6′=48.6′,把48.6′化成度,48.6′=false×48.6=0.81°.
所以26°48′36″=26.81°.
讲解用时:6分钟
解题思路::(1)70.23°实际是70°+0.23°,这里70°不要变,只要将0.23°化为分,然后再把所得的分中的小数部分化为秒.将0.23°化为分,只要用0.23乘以60′即可.
(2)将26°48′36″用度表示,应先将36″化成分,然后再将分化成度就可以了.将36″化成分,可以用false乘以36.
教学建议:要求学生熟练掌握度、分、秒的换算
难度: 3 适应场景:当堂例题 例题来源:无
【练习2.1】
若∠A=20°18′,∠B=20°15′30〞,∠C=20.25°,则( )
∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
【答案】A.
【解析】
解:∵∠A=20°18′,∠B=20°15′30〞,∠C=20.25°=20°15′,
∴∠A>∠B>∠C.故选A.
讲解用时:5分钟
解题思路:∠A、∠B已经是度、分、秒的形式,只要将∠C化为度、分、秒的形式,即可比较大小.
教学建议:两个角比较大小.在比较时要注意统一单位后再比较.
难度: 3 适应场景:当堂练习 例题来源:无
【练习2.2】
3.76°= 度 分 秒;22°32′24″= 度.
【答案】3、45、36、22.54.
【解析】
解:3.76°=3度45分36秒;22°32′24″=22.54度.故填3、45、36、22.54.
讲解用时:5分钟
解题思路:此类题是进行度、分、秒的转化运算,相对比较简单,注意以60为进制.
教学建议:进行度、分、秒的转化运算,注意以60为进制.
难度: 3 适应场景:当堂练习 例题来源:无
【例题3】
计算:18°13′×5﹣49°28′52″÷4
【答案】78°42′47′′
【解析】
解:原式=90°65′﹣48°88′52′′÷4
=90°65′﹣12°22′13′′
=78°42′47′′
讲解用时:6分钟
解题思路:根据度分秒的除法,从大的单位算起,余数乘以进率化成小的单位再除,可得答案.
教学建议:要求学生熟练掌握度、分、秒的换算
难度: 3 适应场景:当堂例题 例题来源:无
【练习3.1】
计算:77°53′26″+33.3°= .
【答案】111°11′26″.
【解析】
解:77°53′26″+33.3°=77°53′26″+33°18′=110°71′26″=111°11′26″.
故答案为:111°11′26″.
讲解用时:5分钟
解题思路:先将33.3°转化为33°18′,然后度与度、分与分、秒和秒对应相加,秒的结果满60转化为分,分的结果满60转化为度.
教学建议:度分秒的换算,注意以60为进制
难度: 3 适应场景:当堂例题 例题来源:无
【例题4】
如图,数一数以O为顶点且小于180°的角一共有多少个?你能得到解这类问题的一般方法吗?
【答案】28个;一般方法为:(n﹣1)+(n﹣2)+…+2+1=.
【解析】
解:7+6+5+4+3+2+1==28,
一般地如果MOG小于180,且图中一共有n条射线,
则小于180°的角一共有:(n﹣1)+(n﹣2)+…+2+1=.
讲解用时:5分钟
解题思路:先根据题意算出以O为顶点且小于180°的角一共有7+6+5+4+3+2+1=28个,然后根据第一问的解法得出一般方法为:(n﹣1)+(n﹣2)+…+2+1=.
教学建议:考查角的大小比较,结合图找出符合条件的角,从而推出解这类问题的一般方法.
难度: 3 适应场景:当堂例题 例题来源:无
【练习4.1】
如图所示,其中最大的角是 ,∠DOC,∠DOB,∠DOA的大小关系是 .
【答案】∠AOD,∠DOA>∠DOB>∠DOC.
【解析】
解:由图可知,最大的角是∠AOD;∠DOA>∠DOB>∠DOC.
故答案为:∠AOD,∠DOA>∠DOB>∠DOC.
讲解用时:5分钟
解题思路:根据图形,结合角的概念与大小比较的方法:度量法和覆盖法,即可得出结论.
教学建议:熟悉角的大小比较的两种方法:度量法和覆盖法.
难度: 3 适应场景:当堂练习 例题来源:无
【例题5】
如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A.∠DOE的度数不能确定 B.∠AOD=∠EOC
C.∠AOD+∠BOE=60° D.∠BOE=2∠COD
【答案】C.
【解析】
解:A、∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠DOE=(∠BOC+∠AOC)=∠AOB=60°.
故本选项叙述错误;
B、∵OD是∠AOC的角平分线,
∴∠AOD=∠AOC.
又∵OC是∠AOB内部任意一条射线,
∴∠AOC=∠EOC不一定成立.
故本选项叙述错误;
C、∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠BOE+∠AOD=∠EOC+∠DOC=∠DOE=(∠BOC+∠AOC)=∠AOB=60°.
故本选项叙述正确;
D、∵OC是∠AOB内部任意一条射线,
∴∠BOE=∠AOC不一定成立,
∴∠BOE=2∠COD不一定成立.
故本选项叙述错误;
故选:C.
讲解用时:5分钟
解题思路:本题是对角的平分线的性质的考查,角平分线将角分成相等的两部分.结合选项得出正确结论.
教学建议:根据角平分线定义得出所求角与已知角的关系转化求解.
难度: 3 适应场景:当堂例题 例题来源:无
【练习5.1】
如图,下列条件中不能确定的是OC是∠AOB的平分线的是
①.∠AOC=∠BOC ②.∠AOB=2∠AOC
③.∠AOC+∠BOC=∠AOB ④.
【答案】①②④.
【解析】
解:①、∠AOC=∠BOC能确定OC平分∠AOB,正确;
②、∠AOB=2∠AOC能确定OC平分∠AOB,正确;
③、∠AOC+∠COB=∠AOB不能确定OC平分∠AOB,错误;
④、∠BOC=∠AOB,能确定OC平分∠AOB,错误.
故正确答案为:①②④.
讲解用时:8分钟
解题思路:直接利用角平分线的性质分别分析得出答案.
教学建议: 正确把握角平分线的定义是解题关键.
难度: 3 适应场景:当堂练习 例题来源:无
【例题6】
已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,求∠MON的大小
【答案】20°或40°.
37522152599690【解析】
解:∠BOC在∠AOB内部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°;
∠BOC在∠AOB外部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB+∠BON=30°+10°=40°.
讲解用时:10分钟
解题思路:根据题意,画出图形,分两种情况讨论:∠BOC在∠AOB内部和外部.
教学建议:考查平分线的性质,注意引导学生分类讨论
难度: 3 适应场景:当堂例题 例题来源:无
【练习6.1】
已知∠AOB=70°,∠BOC=20°,OE为∠AOB的平分线,OF为∠BOC的平分线,则∠EOF= .
【答案】25°或45°.
【解析】
解:(1)当点C在∠AOB的内部时,∠EOF=∠AOB﹣∠BOC=35°﹣10°=25°;
(2)当点C在∠AOB的外部时,∠EOF=∠AOB+∠BOC=35°+10°=45°.
故答案为25°或45°.
讲解用时:5分钟
解题思路:此题分点C在∠AOB的内部和外部两种情况讨论.
教学建议:查角平分线的定义,重点是分类讨论.
难度: 3 适应场景:当堂练习 例题来源:无
【例题7】
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.
【答案】28°.
【解析】
解:设∠AOB=x,∠BOC=2x.则∠AOC=3x.
又OD平分∠AOC,
∴∠AOD=x.
∴∠BOD=∠AOD﹣∠AOB=x﹣x=14°
∴x=28°
即∠AOB=28°.
讲解用时:5分钟
解题思路:此题可以设∠AOB=x,∠BOC=2x,再进一步表示∠AOC=3x,根据角平分线的概念表示∠AOD,最后根据已知角的度数列方程即可计算.
教学建议:考查角平分线的定义.此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算.
难度: 3 适应场景:当堂例题 例题来源:无
【练习7.1】
如图,已知O是直线AB上一点,∠1=20°,OD平分∠BOC,则∠2的度数
是 度.
【答案】80
【解析】
解:如图,∵∠1=20°,∠1+∠BOC=180°,
∴∠BOC=160°.
又∵OD平分∠BOC,
∴∠2=∠BOC=80°;
故填:80.
讲解用时:6分钟
解题思路:首先根据平角角的定义得到∠BOC=160°;然后由角平分线的定义求得∠2=∠BOC.
教学建议:注意此题中隐含着已知条件:∠1+∠BOC=180°.
难度: 3 适应场景:当堂练习 例题来源:无
【例题8】
如图所示,∠AOB:∠BOC:∠COD=4:5:3,OM平分∠AOD,∠BOM=20°,求∠AOD和∠MOC.
【答案】∠AOD=120°,∠MOC=30°.
【解析】
解:设∠AOB=4x,∠BOC=5x,∠COD=3x,
∴∠AOD=12x,
∵OM平分∠AOD,
∴∠AOM=∠AOD=6x,
由题意得,6x﹣4x=20°,
解得,x=10°,
∴∠AOD=12x=120°,∠BOC=5x=50°,
∴∠MOC=∠BOC﹣∠BOM=30°.
讲解用时:8分钟
解题思路:设∠AOB=4x,∠BOC=5x,∠COD=3x,得到∠AOD=12x,根据角平分线的定义得到∠AOM=∠AOD=6x,根据题意列出方程,解方程即可.
教学建议:掌握设未知数求解角度的方法,可类比应用题的求解方式.
难度: 3 适应场景:当堂例题 例题来源:无
【练习8.1】
如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?
【答案】50度
【解析】
解:设∠COD的度数为x,
∵OD是∠COE的平分线,
∴∠EOC=2∠COD=2x,
∵∠BOC比∠COD的2倍还多10°,
∴∠BOC=2x+10°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,
∵∠AOE=140°,
∴2x+4x+20°=140°,解得x=20°,
∴∠BOC=2x+10°=50°
∴∠AOB是50度.
讲解用时:8分钟
解题思路:设∠COD的度数为x,则∠BOC=2x+10°,利用角平分线定义得到∠EOC=2∠COD=2x,∠BOC=2x+10°,再利用OB是∠AOC的平分线得到∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,所以2x+4x+20°=140°,解得x=20°,然后计算2x+10°即可.
教学建议:理解角平分线的定义:灵活应用角平分线的定义进行角度的计算.
难度: 3 适应场景:当堂练习 例题来源:无
0201930
课后作业
【作业1】
如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,试比较下列各角的大小.
(1)∠AOB ∠BOD;
(2)∠AOE ∠AOB;
(3)∠BOD ∠FOB;
(4)∠AOB ∠FOB;
(5)∠DOE ∠BOD.
【答案】(1)>;(2)>;(3)<;(4)=;(5)>.
【解析】
解:(1)∠AOB>∠BOD;
(2)∠AOE>∠AOB;
(3)∠BOD<∠FOB;
(4)∠AOB=∠FOB;
(5)∠DOE>∠BOD.
讲解用时:2分钟
难度: 2 适应场景:练习题 例题来源:无
【作业2】
如图,已知false,false,false______.
59563028575A
B
C
D
O
A
B
C
D
O
【答案】56°.
【解析】
解:由题可知:false.
讲解用时:3分钟
难度: 3 适应场景:练习题 例题来源:无
【作业3】
如图所示,已知点O在直线AB上,∠AOE:∠EOD=1:3,OC是∠BOD的平分线,∠EOC=115°,求∠AOE和∠BOC.
【答案】∠AOE=25°,∠BOC=40°.
【解析】
解:∵∠AOE:∠EOD=1:3,
∴设∠AOE=x,则∠EOD=3x,
又∵∠EOC=115°,
∴∠COD=115°﹣3x,
∵OC是∠BOD的平分线,
∴∠COB=∠COD=115°﹣3x,
又∵点O在直线AB上,
∴∠AOE+∠EOD+∠COD+∠COB=180°,
∴x+3x+2(115﹣3x)=180°,
解得,x=25°,
∴∠AOE=25°,
∴∠BOC=115°﹣3×25°=40°.
讲解用时:8分钟
难度: 3 适应场景:练习题 例题来源:无
第12讲 角的概念与大小比较
0329565
知识定位
讲解用时:5分钟
A、适用范围:人教版初一,基础一般;
B、知识点概述:本讲义主要用于人教版初一新课,主要学习角的概念与大小比较,掌握角的概念及角的表示方法,并能进行角度的互换;能借助三角尺画一些特殊角,掌握角大小的比较方法;会利用角平分线的意义进行有关表示或计算;掌握角的和、差、倍、分关系,并会进行有关计算.
0137160
知识梳理
讲解用时:15分钟
381033020角的定义及其表示方法
角的定义及其表示方法
-57151905(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
角也可以看作是由一条射线绕着它的端点旋转而形成的图形.当终边和始边成一条直线时,形成等角;当终边和始边重合时,形成周角.
(2)角的表示方法:
有四种表示角的方法:
①用一个阿拉伯数字表示单独的一个角,在角内用一段弧标注;
②用一个大写英文字母表示单独的一个角,当角的顶点处有两个或两个以上的角时,不能用这种方法表示角;
③用一个小写希腊字母表示单独的一个角;
④用三个大写英文字母表示任意一个角,这时表示顶点的字母一定要写在中间.
角的理解 (1)角的大小与边的长短无关,只与构成角的两条射线张开的幅度大小有关,角可以度量,可以比较大小,可以进行运算;(2)如果没有特别说明,所说的角都是指小于平角的角.
(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
角也可以看作是由一条射线绕着它的端点旋转而形成的图形.当终边和始边成一条直线时,形成等角;当终边和始边重合时,形成周角.
(2)角的表示方法:
有四种表示角的方法:
①用一个阿拉伯数字表示单独的一个角,在角内用一段弧标注;
②用一个大写英文字母表示单独的一个角,当角的顶点处有两个或两个以上的角时,不能用这种方法表示角;
③用一个小写希腊字母表示单独的一个角;
④用三个大写英文字母表示任意一个角,这时表示顶点的字母一定要写在中间.
角的理解 (1)角的大小与边的长短无关,只与构成角的两条射线张开的幅度大小有关,角可以度量,可以比较大小,可以进行运算;(2)如果没有特别说明,所说的角都是指小于平角的角.
3810143510角的度量与换算
角的度量与换算
133351187451.角度制:以度、分、秒为单位的角的度量制,叫做角度制.
2.角度的换算:
角的度量单位是度、分、秒,把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份就是1分的角,记作1′;把1分的角60等分,每一份就是1秒的角,记作1″.
角度的换算
(1)度、分、秒的换算是60进制,与时间中的时、分、秒的换算相同;
(2)角的度数的换算有两种方法:
①由度化成度、分、秒的形式(即从高位向低位化),用乘法,1°=60′,
1′=60″;
②由度、分、秒化成度的形式(即从低位向高位化),1″=′,1′=°,用除法.
注意:度及度、分、秒之间的转化必须逐级进行转化,“越级”转化容易出错.
1.角度制:以度、分、秒为单位的角的度量制,叫做角度制.
2.角度的换算:
角的度量单位是度、分、秒,把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份就是1分的角,记作1′;把1分的角60等分,每一份就是1秒的角,记作1″.
角度的换算
(1)度、分、秒的换算是60进制,与时间中的时、分、秒的换算相同;
(2)角的度数的换算有两种方法:
①由度化成度、分、秒的形式(即从高位向低位化),用乘法,1°=60′,
1′=60″;
②由度、分、秒化成度的形式(即从低位向高位化),1″=′,1′=°,用除法.
注意:度及度、分、秒之间的转化必须逐级进行转化,“越级”转化容易出错.
-1104902520951.角的比较:
(1)度量法:用量角器量出角的度数,然后按照度数比较角的大小,度数大的角大,度数小的角小;反之,角大度数大,角小度数小.
(2)叠合法:把两个角的顶点和一边分别重合,另一边放在重合边的同旁,通过另一边的位置关系比较大小.
技巧 角的比较 ①在度量法中,注意三点:对中、重合、度数;②在叠合法中,要注意顶点重合,一边重合,另一边落在重合这边的同侧.
1.角的比较:
(1)度量法:用量角器量出角的度数,然后按照度数比较角的大小,度数大的角大,度数小的角小;反之,角大度数大,角小度数小.
(2)叠合法:把两个角的顶点和一边分别重合,另一边放在重合边的同旁,通过另一边的位置关系比较大小.
技巧 角的比较 ①在度量法中,注意三点:对中、重合、度数;②在叠合法中,要注意顶点重合,一边重合,另一边落在重合这边的同侧.
-34290116205角的比较与运算
角的比较与运算
-1962151225552.角的和差:
角的和、差有两种意义,几何意义和代数意义.几何意义对于今后读图形语言有很大帮助,代数意义是今后角的运算的基础.
①几何意义:如图所示,∠AOB与∠BOC的和是∠AOC,表示为∠AOB+∠BOC=∠AOC;∠AOC与∠BOC的差为∠AOB,表示为∠AOC-∠BOC=∠AOB.
②代数意义:如已知∠A=23°17′,∠B=40°50′,∠A+∠B就可以像代数加减法一样计算,即∠A+∠B=23°17′+40°50′=64°7′,∠B-∠A=40°50′-23°17′=17°33′.
3.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.如图所示,射线OC是∠AOB的平分线,则有∠1=∠2=∠AOB或∠AOB=2∠1=2∠2.
角的平分线的理解 角的平分线是一条射线,不是线段,也不是直线,它必须满足下面的条件:
①是从角的顶点引出的射线,且在角的内部;
②把已知角分成了两个角,且这两个角相等.
2.角的和差:
角的和、差有两种意义,几何意义和代数意义.几何意义对于今后读图形语言有很大帮助,代数意义是今后角的运算的基础.
①几何意义:如图所示,∠AOB与∠BOC的和是∠AOC,表示为∠AOB+∠BOC=∠AOC;∠AOC与∠BOC的差为∠AOB,表示为∠AOC-∠BOC=∠AOB.
②代数意义:如已知∠A=23°17′,∠B=40°50′,∠A+∠B就可以像代数加减法一样计算,即∠A+∠B=23°17′+40°50′=64°7′,∠B-∠A=40°50′-23°17′=17°33′.
3.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.如图所示,射线OC是∠AOB的平分线,则有∠1=∠2=∠AOB或∠AOB=2∠1=2∠2.
角的平分线的理解 角的平分线是一条射线,不是线段,也不是直线,它必须满足下面的条件:
①是从角的顶点引出的射线,且在角的内部;
②把已知角分成了两个角,且这两个角相等.
-8572547625 课堂精讲精练
【例题1】
(1)在∠AOB内部画1条射线OC,则图1中有 个不同的角;
(2)在∠AOB内部画2条射线OC,OD,则图2中有 个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有 个不同的角;
【答案】(1)3;(2)6;(3)10.
【解析】
解:(1)在∠AOB内部画1条射线OC,则图中有3个不同的角,
故答案为:3.
(2)在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,
故答案为:6.
(3)在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,
故答案为:10.
讲解用时:5分钟
解题思路:根据角的概念,结合图形,即可数出角的个数.
教学建议:考查了角的有关概念的应用
难度: 3 适应场景:当堂例题 例题来源:无
【练习1.1】
如图所示,下列表示角的方法错误的是( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
【答案】D.
【解析】
解:A、∠1与∠AOB表示同一个角,正确,故本选项错误;
B、∠β表示的是∠BOC,正确,故本选项错误;
C、图中共有三个角:∠AOB,∠AOC,∠BOC,正确,故本选项错误;
D、∠AOC不能用∠O表示,错误,故本选项正确;
故选:D.
讲解用时:3分钟
解题思路:根据角的表示方法表示各个角,再判断即可.
教学建议:本题考查了对角的表示方法的应用,主要检查学生能否正确表示角.
难度: 3 适应场景:当堂练习 例题来源:无
【例题2】
(1)将70.23°用度、分、秒表示;
(2)将26°48′36″用度表示.
【答案】(1)70°13′48″;(2)26.81°.
【解析】
解:(1)将0.23°化为分,可得0.23×60′=13.8′,再把0.8′化为秒,得0.8×60″=48″.
所以70.23°=70°13′48″.
(2)把36″化成分,36″=false×36=0.6′,48′+0.6′=48.6′,把48.6′化成度,48.6′=false×48.6=0.81°.
所以26°48′36″=26.81°.
讲解用时:6分钟
解题思路::(1)70.23°实际是70°+0.23°,这里70°不要变,只要将0.23°化为分,然后再把所得的分中的小数部分化为秒.将0.23°化为分,只要用0.23乘以60′即可.
(2)将26°48′36″用度表示,应先将36″化成分,然后再将分化成度就可以了.将36″化成分,可以用false乘以36.
教学建议:要求学生熟练掌握度、分、秒的换算
难度: 3 适应场景:当堂例题 例题来源:无
【练习2.1】
若∠A=20°18′,∠B=20°15′30〞,∠C=20.25°,则( )
∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
【答案】A.
【解析】
解:∵∠A=20°18′,∠B=20°15′30〞,∠C=20.25°=20°15′,
∴∠A>∠B>∠C.故选A.
讲解用时:5分钟
解题思路:∠A、∠B已经是度、分、秒的形式,只要将∠C化为度、分、秒的形式,即可比较大小.
教学建议:两个角比较大小.在比较时要注意统一单位后再比较.
难度: 3 适应场景:当堂练习 例题来源:无
【练习2.2】
3.76°= 度 分 秒;22°32′24″= 度.
【答案】3、45、36、22.54.
【解析】
解:3.76°=3度45分36秒;22°32′24″=22.54度.故填3、45、36、22.54.
讲解用时:5分钟
解题思路:此类题是进行度、分、秒的转化运算,相对比较简单,注意以60为进制.
教学建议:进行度、分、秒的转化运算,注意以60为进制.
难度: 3 适应场景:当堂练习 例题来源:无
【例题3】
计算:18°13′×5﹣49°28′52″÷4
【答案】78°42′47′′
【解析】
解:原式=90°65′﹣48°88′52′′÷4
=90°65′﹣12°22′13′′
=78°42′47′′
讲解用时:6分钟
解题思路:根据度分秒的除法,从大的单位算起,余数乘以进率化成小的单位再除,可得答案.
教学建议:要求学生熟练掌握度、分、秒的换算
难度: 3 适应场景:当堂例题 例题来源:无
【练习3.1】
计算:77°53′26″+33.3°= .
【答案】111°11′26″.
【解析】
解:77°53′26″+33.3°=77°53′26″+33°18′=110°71′26″=111°11′26″.
故答案为:111°11′26″.
讲解用时:5分钟
解题思路:先将33.3°转化为33°18′,然后度与度、分与分、秒和秒对应相加,秒的结果满60转化为分,分的结果满60转化为度.
教学建议:度分秒的换算,注意以60为进制
难度: 3 适应场景:当堂例题 例题来源:无
【例题4】
如图,数一数以O为顶点且小于180°的角一共有多少个?你能得到解这类问题的一般方法吗?
【答案】28个;一般方法为:(n﹣1)+(n﹣2)+…+2+1=.
【解析】
解:7+6+5+4+3+2+1==28,
一般地如果MOG小于180,且图中一共有n条射线,
则小于180°的角一共有:(n﹣1)+(n﹣2)+…+2+1=.
讲解用时:5分钟
解题思路:先根据题意算出以O为顶点且小于180°的角一共有7+6+5+4+3+2+1=28个,然后根据第一问的解法得出一般方法为:(n﹣1)+(n﹣2)+…+2+1=.
教学建议:考查角的大小比较,结合图找出符合条件的角,从而推出解这类问题的一般方法.
难度: 3 适应场景:当堂例题 例题来源:无
【练习4.1】
如图所示,其中最大的角是 ,∠DOC,∠DOB,∠DOA的大小关系是 .
【答案】∠AOD,∠DOA>∠DOB>∠DOC.
【解析】
解:由图可知,最大的角是∠AOD;∠DOA>∠DOB>∠DOC.
故答案为:∠AOD,∠DOA>∠DOB>∠DOC.
讲解用时:5分钟
解题思路:根据图形,结合角的概念与大小比较的方法:度量法和覆盖法,即可得出结论.
教学建议:熟悉角的大小比较的两种方法:度量法和覆盖法.
难度: 3 适应场景:当堂练习 例题来源:无
【例题5】
如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A.∠DOE的度数不能确定 B.∠AOD=∠EOC
C.∠AOD+∠BOE=60° D.∠BOE=2∠COD
【答案】C.
【解析】
解:A、∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠DOE=(∠BOC+∠AOC)=∠AOB=60°.
故本选项叙述错误;
B、∵OD是∠AOC的角平分线,
∴∠AOD=∠AOC.
又∵OC是∠AOB内部任意一条射线,
∴∠AOC=∠EOC不一定成立.
故本选项叙述错误;
C、∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠BOE+∠AOD=∠EOC+∠DOC=∠DOE=(∠BOC+∠AOC)=∠AOB=60°.
故本选项叙述正确;
D、∵OC是∠AOB内部任意一条射线,
∴∠BOE=∠AOC不一定成立,
∴∠BOE=2∠COD不一定成立.
故本选项叙述错误;
故选:C.
讲解用时:5分钟
解题思路:本题是对角的平分线的性质的考查,角平分线将角分成相等的两部分.结合选项得出正确结论.
教学建议:根据角平分线定义得出所求角与已知角的关系转化求解.
难度: 3 适应场景:当堂例题 例题来源:无
【练习5.1】
如图,下列条件中不能确定的是OC是∠AOB的平分线的是
①.∠AOC=∠BOC ②.∠AOB=2∠AOC
③.∠AOC+∠BOC=∠AOB ④.
【答案】①②④.
【解析】
解:①、∠AOC=∠BOC能确定OC平分∠AOB,正确;
②、∠AOB=2∠AOC能确定OC平分∠AOB,正确;
③、∠AOC+∠COB=∠AOB不能确定OC平分∠AOB,错误;
④、∠BOC=∠AOB,能确定OC平分∠AOB,错误.
故正确答案为:①②④.
讲解用时:8分钟
解题思路:直接利用角平分线的性质分别分析得出答案.
教学建议: 正确把握角平分线的定义是解题关键.
难度: 3 适应场景:当堂练习 例题来源:无
【例题6】
已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,求∠MON的大小
【答案】20°或40°.
37522152599690【解析】
解:∠BOC在∠AOB内部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°;
∠BOC在∠AOB外部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB+∠BON=30°+10°=40°.
讲解用时:10分钟
解题思路:根据题意,画出图形,分两种情况讨论:∠BOC在∠AOB内部和外部.
教学建议:考查平分线的性质,注意引导学生分类讨论
难度: 3 适应场景:当堂例题 例题来源:无
【练习6.1】
已知∠AOB=70°,∠BOC=20°,OE为∠AOB的平分线,OF为∠BOC的平分线,则∠EOF= .
【答案】25°或45°.
【解析】
解:(1)当点C在∠AOB的内部时,∠EOF=∠AOB﹣∠BOC=35°﹣10°=25°;
(2)当点C在∠AOB的外部时,∠EOF=∠AOB+∠BOC=35°+10°=45°.
故答案为25°或45°.
讲解用时:5分钟
解题思路:此题分点C在∠AOB的内部和外部两种情况讨论.
教学建议:查角平分线的定义,重点是分类讨论.
难度: 3 适应场景:当堂练习 例题来源:无
【例题7】
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.
【答案】28°.
【解析】
解:设∠AOB=x,∠BOC=2x.则∠AOC=3x.
又OD平分∠AOC,
∴∠AOD=x.
∴∠BOD=∠AOD﹣∠AOB=x﹣x=14°
∴x=28°
即∠AOB=28°.
讲解用时:5分钟
解题思路:此题可以设∠AOB=x,∠BOC=2x,再进一步表示∠AOC=3x,根据角平分线的概念表示∠AOD,最后根据已知角的度数列方程即可计算.
教学建议:考查角平分线的定义.此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算.
难度: 3 适应场景:当堂例题 例题来源:无
【练习7.1】
如图,已知O是直线AB上一点,∠1=20°,OD平分∠BOC,则∠2的度数
是 度.
【答案】80
【解析】
解:如图,∵∠1=20°,∠1+∠BOC=180°,
∴∠BOC=160°.
又∵OD平分∠BOC,
∴∠2=∠BOC=80°;
故填:80.
讲解用时:6分钟
解题思路:首先根据平角角的定义得到∠BOC=160°;然后由角平分线的定义求得∠2=∠BOC.
教学建议:注意此题中隐含着已知条件:∠1+∠BOC=180°.
难度: 3 适应场景:当堂练习 例题来源:无
【例题8】
如图所示,∠AOB:∠BOC:∠COD=4:5:3,OM平分∠AOD,∠BOM=20°,求∠AOD和∠MOC.
【答案】∠AOD=120°,∠MOC=30°.
【解析】
解:设∠AOB=4x,∠BOC=5x,∠COD=3x,
∴∠AOD=12x,
∵OM平分∠AOD,
∴∠AOM=∠AOD=6x,
由题意得,6x﹣4x=20°,
解得,x=10°,
∴∠AOD=12x=120°,∠BOC=5x=50°,
∴∠MOC=∠BOC﹣∠BOM=30°.
讲解用时:8分钟
解题思路:设∠AOB=4x,∠BOC=5x,∠COD=3x,得到∠AOD=12x,根据角平分线的定义得到∠AOM=∠AOD=6x,根据题意列出方程,解方程即可.
教学建议:掌握设未知数求解角度的方法,可类比应用题的求解方式.
难度: 3 适应场景:当堂例题 例题来源:无
【练习8.1】
如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?
【答案】50度
【解析】
解:设∠COD的度数为x,
∵OD是∠COE的平分线,
∴∠EOC=2∠COD=2x,
∵∠BOC比∠COD的2倍还多10°,
∴∠BOC=2x+10°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,
∵∠AOE=140°,
∴2x+4x+20°=140°,解得x=20°,
∴∠BOC=2x+10°=50°
∴∠AOB是50度.
讲解用时:8分钟
解题思路:设∠COD的度数为x,则∠BOC=2x+10°,利用角平分线定义得到∠EOC=2∠COD=2x,∠BOC=2x+10°,再利用OB是∠AOC的平分线得到∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,所以2x+4x+20°=140°,解得x=20°,然后计算2x+10°即可.
教学建议:理解角平分线的定义:灵活应用角平分线的定义进行角度的计算.
难度: 3 适应场景:当堂练习 例题来源:无
0201930
课后作业
【作业1】
如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,试比较下列各角的大小.
(1)∠AOB ∠BOD;
(2)∠AOE ∠AOB;
(3)∠BOD ∠FOB;
(4)∠AOB ∠FOB;
(5)∠DOE ∠BOD.
【答案】(1)>;(2)>;(3)<;(4)=;(5)>.
【解析】
解:(1)∠AOB>∠BOD;
(2)∠AOE>∠AOB;
(3)∠BOD<∠FOB;
(4)∠AOB=∠FOB;
(5)∠DOE>∠BOD.
讲解用时:2分钟
难度: 2 适应场景:练习题 例题来源:无
【作业2】
如图,已知false,false,false______.
59563028575A
B
C
D
O
A
B
C
D
O
【答案】56°.
【解析】
解:由题可知:false.
讲解用时:3分钟
难度: 3 适应场景:练习题 例题来源:无
【作业3】
如图所示,已知点O在直线AB上,∠AOE:∠EOD=1:3,OC是∠BOD的平分线,∠EOC=115°,求∠AOE和∠BOC.
【答案】∠AOE=25°,∠BOC=40°.
【解析】
解:∵∠AOE:∠EOD=1:3,
∴设∠AOE=x,则∠EOD=3x,
又∵∠EOC=115°,
∴∠COD=115°﹣3x,
∵OC是∠BOD的平分线,
∴∠COB=∠COD=115°﹣3x,
又∵点O在直线AB上,
∴∠AOE+∠EOD+∠COD+∠COB=180°,
∴x+3x+2(115﹣3x)=180°,
解得,x=25°,
∴∠AOE=25°,
∴∠BOC=115°﹣3×25°=40°.
讲解用时:8分钟
难度: 3 适应场景:练习题 例题来源:无
