2020年秋人教版八年级数学上册暑期课程跟踪——11.1.1三角形的边提优练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册暑期课程跟踪——11.1.1三角形的边提优练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 122.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 23:57:35 | ||
图片预览

文档简介
11.1.1三角形的边提优练习
一、选择题
1.
下面给出的三条线段,一定不能组成三角形的是( )
A.
a+1,a+2,a+3(a>0)
B.
三条线段的比为4∶6∶10
C.
3cm,8cm,10cm
D.
3a,5a,2a+1(a>0)
2.已知三角形的周长为9,且三边长都是整数,则满足条件的三角形共有(
)
A.2个
B.3个
C.4个
D.5个
3.
如图,在△ABF中,∠B的对边是( )
A.
AD
B.
AE
C.
AF
D.
AC
4.
已知三角形的两边分别为1和4,第三边长为整数
,则该三角形的周长为(
)
A.7
B.8
C.9
D.10
5.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度,
要钉成一个三角形木架,应在下列四根木棒中选取
(
)
A.10cm的木棒
B.20cm的木棒;
C.50cm的木棒
D.60cm的木棒
6.
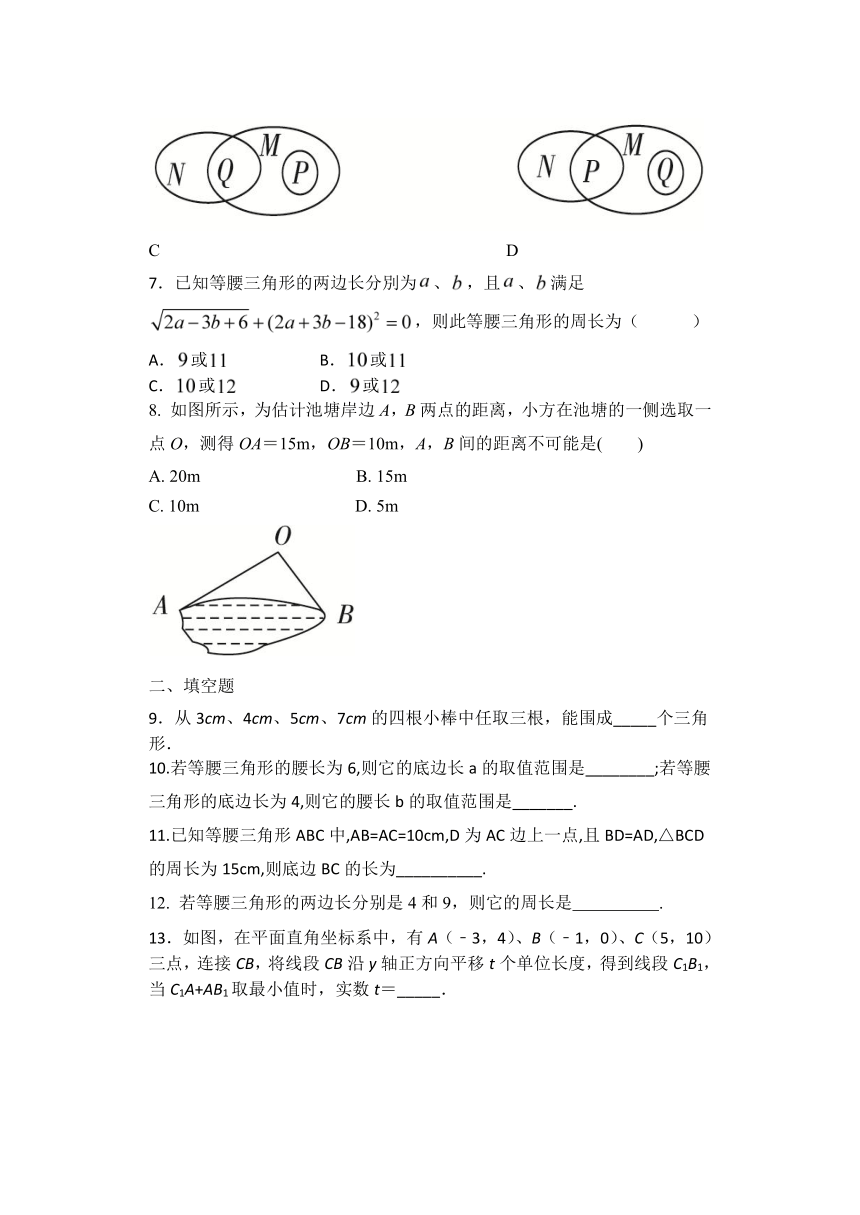
设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个选项中,能表示它们之间关系的是( )
A
B
C
D
7.已知等腰三角形的两边长分別为、,且、满足,则此等腰三角形的周长为(
)
A.或
B.或
C.或
D.或
8.
如图所示,为估计池塘岸边A,B两点的距离,小方在池塘的一侧选取一点O,测得OA=15m,OB=10m,A,B间的距离不可能是( )
A.
20m
B.
15m
C.
10m
D.
5m
二、填空题
9.从3cm、4cm、5cm、7cm的四根小棒中任取三根,能围成_____个三角形.
10.若等腰三角形的腰长为6,则它的底边长a的取值范围是________;若等腰三角形的底边长为4,则它的腰长b的取值范围是_______.
11.已知等腰三角形ABC中,AB=AC=10cm,D为AC边上一点,且BD=AD,△BCD的周长为15cm,则底边BC的长为__________.
12.
若等腰三角形的两边长分别是4和9,则它的周长是
.
13.如图,在平面直角坐标系中,有A(﹣3,4)、B(﹣1,0)、C(5,10)三点,连接CB,将线段CB沿y轴正方向平移t个单位长度,得到线段C1B1,当C1A+AB1取最小值时,实数t=_____.
14.两根木棒的长分别是8cm,10cm,要选择第三根木棒将它们钉成三角形,那么第三根木棒的长x的取值范围是________;如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________.
三、解答题
15.
图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.
16.设△ABC的三边a,b,c的长度都是自然数,且a≤b≤c,a+b+c=13,则以a,b,c
为边的三角形共多少?
17.
已知在△ABC中,AB=AC,D在AC的延长线上.
求证:BD-BC<AD-AB.
18.如果是的三边,化简:.
19.
如图,是由6个面积为1的小正方形组成的长方形,点A,B,C,D,E,F,G是小正方形的顶点,以这7个点中的任意3个点为顶点,可组成多少个面积为1的三角形?请写出所有这样的三角形.
20.王老师在黑板上写了一道题:如图1,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,试比较AC+BD与AB的大小.小聪思考片刻就想出来了,他说将AB平移到CE位置,如图2,连接BE,DE,就可以比较AC+BD与AB的大小了,你知道他是怎样比较的吗?
答案
1.
B
2.
B
3.
C
4.C
5.
B
6.
A
7.
B
8.
B
9.
3
10.
0b>2
11.
5cm
12.
22
13.
14.
2cm25cm.
15.
解:共有6个三角形,其中锐角三角形有2个:△ABE,△ABC;直角三角形有3个:△ABD,△ADE,△ADC;钝角三角形有1个:△AEC.
16.
5个
17.
证明:∵AB=AC,AD=AC+CD,∴AD-AB=AC+CD-AC=CD,∵在△BCD中,BD-BC<CD,∴BD-BC<AD-AB.
18.
解∵是的三边,
∴,,,
∴,,,
∴原式
.
19.
解:共有14个三角形,以这7个点中的任意3个点为顶点,组成面积为1的三角形,只需三角形的底是1,高是2或三角形的底是2,高是1.符合要求的三角形为△ADE,△BDE,△AEF,△BEF,
△BFG,△AFG,△ABD,△ABE,△ABF,△ABG,△DCF,△ECG,△BCF,△ACG
20.
解由平移的性质知,AB与CE平行且相等,BE=AC,
当B,D,E三点不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,AB=CE,AB=CD,
∴△CED是等边三角形,∴DE=AB,
根据三角形的三边关系知BE+BD=AC+BD>DE=AB,即AC+BD>AB;
当B,D,E三点共线时,AC+BD=AB,
∴AC+BD≥AB.
一、选择题
1.
下面给出的三条线段,一定不能组成三角形的是( )
A.
a+1,a+2,a+3(a>0)
B.
三条线段的比为4∶6∶10
C.
3cm,8cm,10cm
D.
3a,5a,2a+1(a>0)
2.已知三角形的周长为9,且三边长都是整数,则满足条件的三角形共有(
)
A.2个
B.3个
C.4个
D.5个
3.
如图,在△ABF中,∠B的对边是( )
A.
AD
B.
AE
C.
AF
D.
AC
4.
已知三角形的两边分别为1和4,第三边长为整数
,则该三角形的周长为(
)
A.7
B.8
C.9
D.10
5.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度,
要钉成一个三角形木架,应在下列四根木棒中选取
(
)
A.10cm的木棒
B.20cm的木棒;
C.50cm的木棒
D.60cm的木棒
6.
设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个选项中,能表示它们之间关系的是( )
A
B
C
D
7.已知等腰三角形的两边长分別为、,且、满足,则此等腰三角形的周长为(
)
A.或
B.或
C.或
D.或
8.
如图所示,为估计池塘岸边A,B两点的距离,小方在池塘的一侧选取一点O,测得OA=15m,OB=10m,A,B间的距离不可能是( )
A.
20m
B.
15m
C.
10m
D.
5m
二、填空题
9.从3cm、4cm、5cm、7cm的四根小棒中任取三根,能围成_____个三角形.
10.若等腰三角形的腰长为6,则它的底边长a的取值范围是________;若等腰三角形的底边长为4,则它的腰长b的取值范围是_______.
11.已知等腰三角形ABC中,AB=AC=10cm,D为AC边上一点,且BD=AD,△BCD的周长为15cm,则底边BC的长为__________.
12.
若等腰三角形的两边长分别是4和9,则它的周长是
.
13.如图,在平面直角坐标系中,有A(﹣3,4)、B(﹣1,0)、C(5,10)三点,连接CB,将线段CB沿y轴正方向平移t个单位长度,得到线段C1B1,当C1A+AB1取最小值时,实数t=_____.
14.两根木棒的长分别是8cm,10cm,要选择第三根木棒将它们钉成三角形,那么第三根木棒的长x的取值范围是________;如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________.
三、解答题
15.
图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.
16.设△ABC的三边a,b,c的长度都是自然数,且a≤b≤c,a+b+c=13,则以a,b,c
为边的三角形共多少?
17.
已知在△ABC中,AB=AC,D在AC的延长线上.
求证:BD-BC<AD-AB.
18.如果是的三边,化简:.
19.
如图,是由6个面积为1的小正方形组成的长方形,点A,B,C,D,E,F,G是小正方形的顶点,以这7个点中的任意3个点为顶点,可组成多少个面积为1的三角形?请写出所有这样的三角形.
20.王老师在黑板上写了一道题:如图1,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,试比较AC+BD与AB的大小.小聪思考片刻就想出来了,他说将AB平移到CE位置,如图2,连接BE,DE,就可以比较AC+BD与AB的大小了,你知道他是怎样比较的吗?
答案
1.
B
2.
B
3.
C
4.C
5.
B
6.
A
7.
B
8.
B
9.
3
10.
0
11.
5cm
12.
22
13.
14.
2cm
15.
解:共有6个三角形,其中锐角三角形有2个:△ABE,△ABC;直角三角形有3个:△ABD,△ADE,△ADC;钝角三角形有1个:△AEC.
16.
5个
17.
证明:∵AB=AC,AD=AC+CD,∴AD-AB=AC+CD-AC=CD,∵在△BCD中,BD-BC<CD,∴BD-BC<AD-AB.
18.
解∵是的三边,
∴,,,
∴,,,
∴原式
.
19.
解:共有14个三角形,以这7个点中的任意3个点为顶点,组成面积为1的三角形,只需三角形的底是1,高是2或三角形的底是2,高是1.符合要求的三角形为△ADE,△BDE,△AEF,△BEF,
△BFG,△AFG,△ABD,△ABE,△ABF,△ABG,△DCF,△ECG,△BCF,△ACG
20.
解由平移的性质知,AB与CE平行且相等,BE=AC,
当B,D,E三点不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,AB=CE,AB=CD,
∴△CED是等边三角形,∴DE=AB,
根据三角形的三边关系知BE+BD=AC+BD>DE=AB,即AC+BD>AB;
当B,D,E三点共线时,AC+BD=AB,
∴AC+BD≥AB.
