2020年秋人教版八年级数学上册暑期课程跟踪——11.1.2 三角形的高、中线与角平分线提优练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册暑期课程跟踪——11.1.2 三角形的高、中线与角平分线提优练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 00:00:00 | ||
图片预览


文档简介
11.1.2
三角形的高、中线与角平分线提优练习
一、选择题
1.
以下关于三角形中线的说法正确的是( )
A.
三角形三条中线的交点在三角形的内部、外部或一边上
B.
若BE是△ABC的一条中线,则BE=AC
C.
若AD是△ABC的一条中线,则△ABD和△ADC的面积一定相等
D.
若CF是△ABC的一条中线,则AB=AF
2.如图,在是两条中线,则(
)
A.1∶2
B.2∶3
C.1∶3
D.1∶4
3.
如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能确定
4.点P是△ABC内一点,且P到△ABC的三边距离相等,则P是△ABC哪三条线的交点( )
A.边的垂直平分线
B.角平分线
C.高线
D.中位线
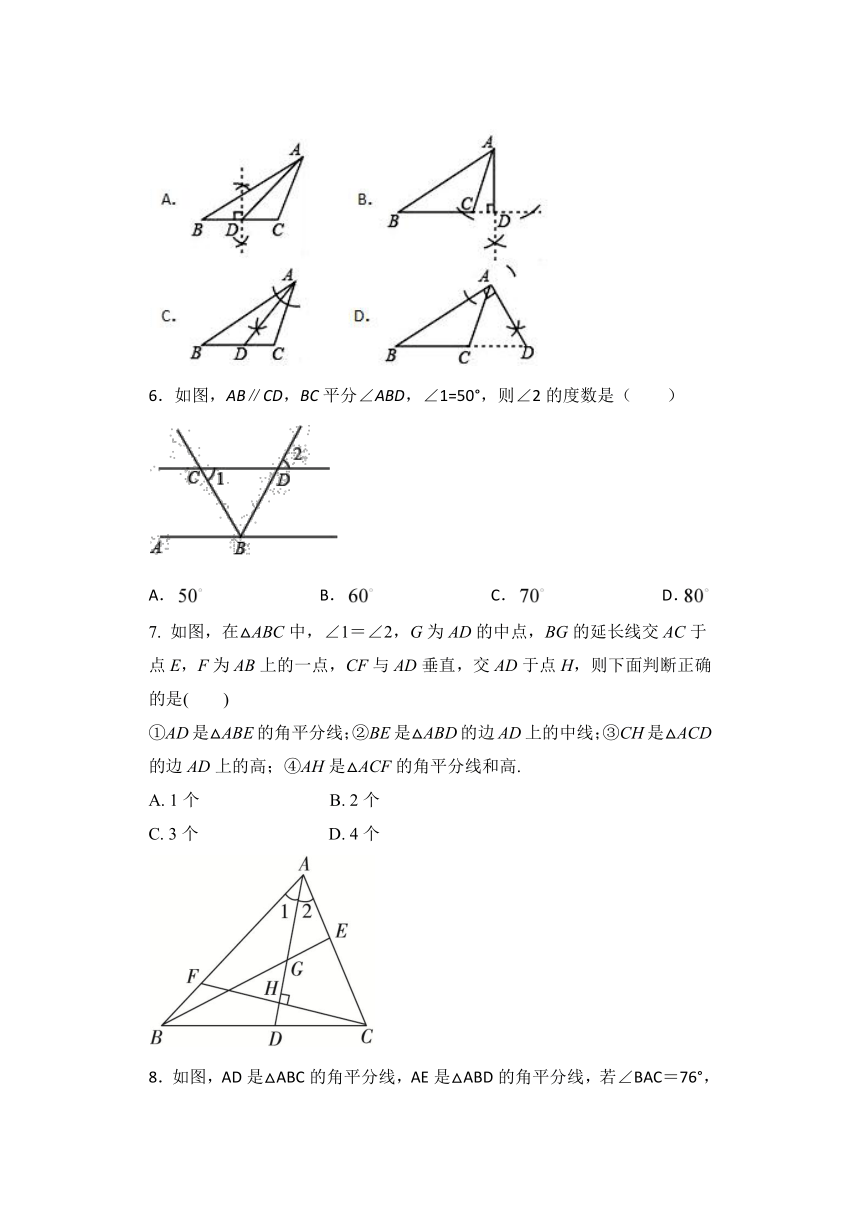
5.下列尺规作图,能判断AD是△ABC边上的高是( )
6.如图,AB∥CD,BC平分∠ABD,∠1=50°,则∠2的度数是( )
A.
B.
C.
D.
7.
如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的是( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高.
A.
1个
B.
2个
C.
3个
D.
4个
8.如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=76°,则∠EAD的度数是(
)
A.19°
B.20°
C.18°
D.28°
二、填空题
9.如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是1,那么△A1B1C1的面积为____.
10.
如图,在△ABC中,AD为BC边上的中线,点F,E是AD的三等分点,若△ABC的面积为12cm2,则图中阴影部分的面积为
.
11.如图,Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线交于点O,OM⊥AB于M,若OM=4,S△ABC=180,则△ABC的周长是_____.
12.如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为_____.
三、解答题
13.(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是________,△EBD的面积是________.
(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?
14.
如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
15.
在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,图中出现三个不同的直角三角形(3=2×1+1),又在△ABD中作AB边上的高DD1,这时图中便出现五个不同的直角三角形(5=2×2+1);按同样的方法作D1D2,D2D3,D3D4,…,Dk-1Dk,当作出Dk-1Dk时,图中有多少个不同的直角三角形?
16.如图,∠ACB=90°,BD平分∠ABE,CD∥AB交BD于D,∠1=20°,求∠2的度数.
答案
1.
C
2.
D
3.
B
4.
B
5.
B
6.
D
7.
B
8.
A
9.
7
10.
6cm2
11.
90
12.
3
13.
解:(1)∵点D,E,F分别是BC,AB,AC的中点,三角形中线等分三角形的面积,
∴S△ABD=S△ABC=×16=8,
S△EBD=S△ABD=×8=4,
故答案为:8,4;
(2)∵在△ABC中,D是BC边的中点,
∴S△ABD=S△ABC=8,
∵E是AD的中点,
∴S△BED=S△ABD=4,
同理得,S△CDE=4;
∴S△BCE=8,
∵F是CE的中点,
∴S△BEF=S△BCE=4.
14.
解:∵AD是BC边上的中线,∴BD=CD.设BD=CD=x,AB=y.∵AC=2BC,∴AC=4x.分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得x=12,y=28,即AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得x=8,y=52,即AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系.综上所述,AC=48,AB=28.
15.
解:作出AD时,有2×1+1=3(个)不同的直角三角形;作出DD1时,有2×2+1=5(个)不同的直角三角形;作出D1D2时,有2×3+1=7(个)不同的直角三角形;作出D2D3时,有2×4+1=9(个)
不同的直角三角形;….
作出Dk-1Dk时,有2(k+1)+1=2k+3(个)不同的直角三角形
16.
解∵BD平分∠ABE,∠1=20°,
∴∠ABC=2∠1=40°,
∵CD∥AB,
∴∠DCE=∠ABC=40°,
∵∠ACB=90°,
∴∠2=90°-40°=50°.
三角形的高、中线与角平分线提优练习
一、选择题
1.
以下关于三角形中线的说法正确的是( )
A.
三角形三条中线的交点在三角形的内部、外部或一边上
B.
若BE是△ABC的一条中线,则BE=AC
C.
若AD是△ABC的一条中线,则△ABD和△ADC的面积一定相等
D.
若CF是△ABC的一条中线,则AB=AF
2.如图,在是两条中线,则(
)
A.1∶2
B.2∶3
C.1∶3
D.1∶4
3.
如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能确定
4.点P是△ABC内一点,且P到△ABC的三边距离相等,则P是△ABC哪三条线的交点( )
A.边的垂直平分线
B.角平分线
C.高线
D.中位线
5.下列尺规作图,能判断AD是△ABC边上的高是( )
6.如图,AB∥CD,BC平分∠ABD,∠1=50°,则∠2的度数是( )
A.
B.
C.
D.
7.
如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的是( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高.
A.
1个
B.
2个
C.
3个
D.
4个
8.如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=76°,则∠EAD的度数是(
)
A.19°
B.20°
C.18°
D.28°
二、填空题
9.如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是1,那么△A1B1C1的面积为____.
10.
如图,在△ABC中,AD为BC边上的中线,点F,E是AD的三等分点,若△ABC的面积为12cm2,则图中阴影部分的面积为
.
11.如图,Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线交于点O,OM⊥AB于M,若OM=4,S△ABC=180,则△ABC的周长是_____.
12.如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为_____.
三、解答题
13.(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是________,△EBD的面积是________.
(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?
14.
如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
15.
在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,图中出现三个不同的直角三角形(3=2×1+1),又在△ABD中作AB边上的高DD1,这时图中便出现五个不同的直角三角形(5=2×2+1);按同样的方法作D1D2,D2D3,D3D4,…,Dk-1Dk,当作出Dk-1Dk时,图中有多少个不同的直角三角形?
16.如图,∠ACB=90°,BD平分∠ABE,CD∥AB交BD于D,∠1=20°,求∠2的度数.
答案
1.
C
2.
D
3.
B
4.
B
5.
B
6.
D
7.
B
8.
A
9.
7
10.
6cm2
11.
90
12.
3
13.
解:(1)∵点D,E,F分别是BC,AB,AC的中点,三角形中线等分三角形的面积,
∴S△ABD=S△ABC=×16=8,
S△EBD=S△ABD=×8=4,
故答案为:8,4;
(2)∵在△ABC中,D是BC边的中点,
∴S△ABD=S△ABC=8,
∵E是AD的中点,
∴S△BED=S△ABD=4,
同理得,S△CDE=4;
∴S△BCE=8,
∵F是CE的中点,
∴S△BEF=S△BCE=4.
14.
解:∵AD是BC边上的中线,∴BD=CD.设BD=CD=x,AB=y.∵AC=2BC,∴AC=4x.分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得x=12,y=28,即AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得x=8,y=52,即AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系.综上所述,AC=48,AB=28.
15.
解:作出AD时,有2×1+1=3(个)不同的直角三角形;作出DD1时,有2×2+1=5(个)不同的直角三角形;作出D1D2时,有2×3+1=7(个)不同的直角三角形;作出D2D3时,有2×4+1=9(个)
不同的直角三角形;….
作出Dk-1Dk时,有2(k+1)+1=2k+3(个)不同的直角三角形
16.
解∵BD平分∠ABE,∠1=20°,
∴∠ABC=2∠1=40°,
∵CD∥AB,
∴∠DCE=∠ABC=40°,
∵∠ACB=90°,
∴∠2=90°-40°=50°.
