人教版 七年级(上)数学讲义 4.2 直线、射线、线段 (含解析)
文档属性
| 名称 | 人教版 七年级(上)数学讲义 4.2 直线、射线、线段 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览



文档简介
69532585725
第12讲 直线、射线、线段
0329565
知识定位
讲解用时:5分钟
A、适用范围:人教版初一,基础一般;
B、知识点概述:本讲义主要用于人教版初一新课,主要学习直线、射线与线段,理解直线、射线、线段的概念,掌握它们的区别和联系;利用直线、线段的性质解决相关实际问题;利用线段的和差倍分解决相关计算问题.
0137160
知识梳理
讲解用时:15分钟
381033020直线
直线
-57151905(1)概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始的概念,直线常用“一根拉得很紧的细线”,“一张纸的折痕”等实际事物进行描述.
(2)特点:直线向两方无限延伸,不可度量,没有粗细;并且同一平面内的两条相交直线只有一个交点.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.即“两点确定一条直线”.
(4)直线的两种表示法:一是用一个小写字母表示:如直线a,b,c或直线l等.另一个是用直线上两个点的大写字母表示,如:直线AB或直线BA.如图:表示为直线l或直线AB(点的字母位置可以交换).
(5)直线与点的位置关系:一是点在直线上,也叫做直线经过这点;另一种是点在直线外,也叫做直线不经过这个点.
(1)概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始的概念,直线常用“一根拉得很紧的细线”,“一张纸的折痕”等实际事物进行描述.
(2)特点:直线向两方无限延伸,不可度量,没有粗细;并且同一平面内的两条相交直线只有一个交点.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.即“两点确定一条直线”.
(4)直线的两种表示法:一是用一个小写字母表示:如直线a,b,c或直线l等.另一个是用直线上两个点的大写字母表示,如:直线AB或直线BA.如图:表示为直线l或直线AB(点的字母位置可以交换).
(5)直线与点的位置关系:一是点在直线上,也叫做直线经过这点;另一种是点在直线外,也叫做直线不经过这个点.
3810143510射线
射线
13335118745(1)定义:直线上一点和它一旁的部分,叫做射线.它是直线的一部分.如图就是一条射线,其中O是射线的端点.
(2)表示法:同直线一样,射线也有两种表示方法,一种是用一个小写字母表示:如射线a,b,c或射线l等,另一个是用射线上两个点的大写字母表示,其中前面的字母表示的点必须是端点.如图:表示为射线l或射线OA.
注意:表示射线端点的字母一定要写在前面.
(3)特点:射线只有1个端点,向一方无限延伸,因此不可度量.
(1)定义:直线上一点和它一旁的部分,叫做射线.它是直线的一部分.如图就是一条射线,其中O是射线的端点.
(2)表示法:同直线一样,射线也有两种表示方法,一种是用一个小写字母表示:如射线a,b,c或射线l等,另一个是用射线上两个点的大写字母表示,其中前面的字母表示的点必须是端点.如图:表示为射线l或射线OA.
注意:表示射线端点的字母一定要写在前面.
(3)特点:射线只有1个端点,向一方无限延伸,因此不可度量.
-139065107315(1)定义:直线上两点和它们之间的部分,叫做线段.它是直线的一部分.
(2)特点:有两个端点,不能向两方无限延伸,因此它有长度,有大小.
(3)表示法:同直线一样,线段也有两种表示法,一种是用一个小写字母表示,如线段a,b,c.另一种是用线段两个端点的大写字母表示.如图:可以表示为:线段AB或线段BA,或线段a.
(4)线段的基本性质:两点的所有连线中,线段最短,简单的说成:“两点之间,线段最短.”意义:选取最短路线的原则和依据.
(5)两点间的距离:连接两点的线段的长度,叫做这两点间的距离.
注意 线段的表示 表示线段的两端点的字母可以交换,如线段AB也是线段BA,但端点字母不同线段就不一样.
(1)定义:直线上两点和它们之间的部分,叫做线段.它是直线的一部分.
(2)特点:有两个端点,不能向两方无限延伸,因此它有长度,有大小.
(3)表示法:同直线一样,线段也有两种表示法,一种是用一个小写字母表示,如线段a,b,c.另一种是用线段两个端点的大写字母表示.如图:可以表示为:线段AB或线段BA,或线段a.
(4)线段的基本性质:两点的所有连线中,线段最短,简单的说成:“两点之间,线段最短.”意义:选取最短路线的原则和依据.
(5)两点间的距离:连接两点的线段的长度,叫做这两点间的距离.
注意 线段的表示 表示线段的两端点的字母可以交换,如线段AB也是线段BA,但端点字母不同线段就不一样.
-34290112395线段
线段
1333566040线段的画法
线段的画法
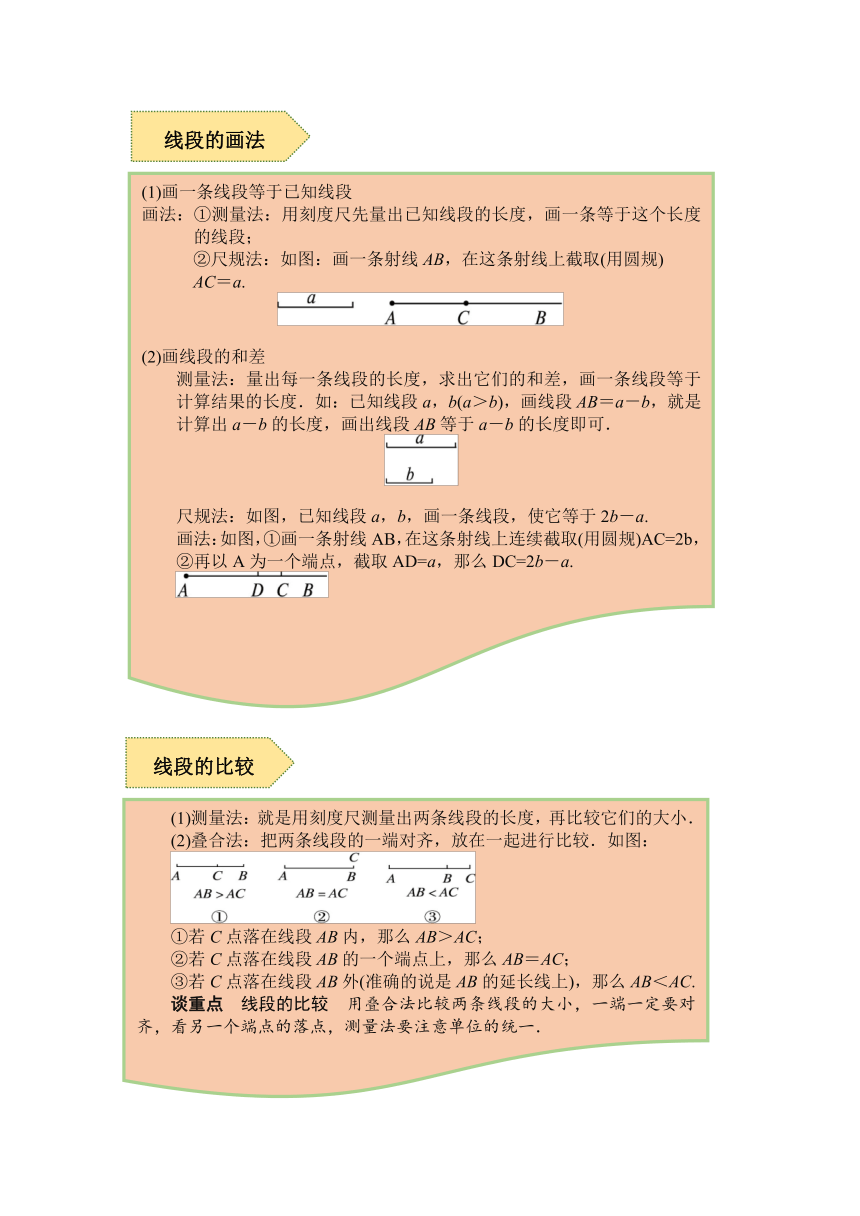
-5715213995(1)画一条线段等于已知线段
画法:①测量法:用刻度尺先量出已知线段的长度,画一条等于这个长度的线段;
②尺规法:如图:画一条射线AB,在这条射线上截取(用圆规)
AC=a.
(2)画线段的和差
测量法:量出每一条线段的长度,求出它们的和差,画一条线段等于计算结果的长度.如:已知线段a,b(a>b),画线段AB=a-b,就是计算出a-b的长度,画出线段AB等于a-b的长度即可.
尺规法:如图,已知线段a,b,画一条线段,使它等于2b-a.
画法:如图,①画一条射线AB,在这条射线上连续截取(用圆规)AC=2b,
②再以A为一个端点,截取AD=a,那么DC=2b-a.
(1)画一条线段等于已知线段
画法:①测量法:用刻度尺先量出已知线段的长度,画一条等于这个长度的线段;
②尺规法:如图:画一条射线AB,在这条射线上截取(用圆规)
AC=a.
(2)画线段的和差
测量法:量出每一条线段的长度,求出它们的和差,画一条线段等于计算结果的长度.如:已知线段a,b(a>b),画线段AB=a-b,就是计算出a-b的长度,画出线段AB等于a-b的长度即可.
尺规法:如图,已知线段a,b,画一条线段,使它等于2b-a.
画法:如图,①画一条射线AB,在这条射线上连续截取(用圆规)AC=2b,
②再以A为一个端点,截取AD=a,那么DC=2b-a.
-3429025400线段的比较
线段的比较
-53340172085(1)测量法:就是用刻度尺测量出两条线段的长度,再比较它们的大小.
(2)叠合法:把两条线段的一端对齐,放在一起进行比较.如图:
①若C点落在线段AB内,那么AB>AC;
②若C点落在线段AB的一个端点上,那么AB=AC;
③若C点落在线段AB外(准确的说是AB的延长线上),那么AB<AC.
谈重点 线段的比较 用叠合法比较两条线段的大小,一端一定要对齐,看另一个端点的落点,测量法要注意单位的统一.
(1)测量法:就是用刻度尺测量出两条线段的长度,再比较它们的大小.
(2)叠合法:把两条线段的一端对齐,放在一起进行比较.如图:
①若C点落在线段AB内,那么AB>AC;
②若C点落在线段AB的一个端点上,那么AB=AC;
③若C点落在线段AB外(准确的说是AB的延长线上),那么AB<AC.
谈重点 线段的比较 用叠合法比较两条线段的大小,一端一定要对齐,看另一个端点的落点,测量法要注意单位的统一.
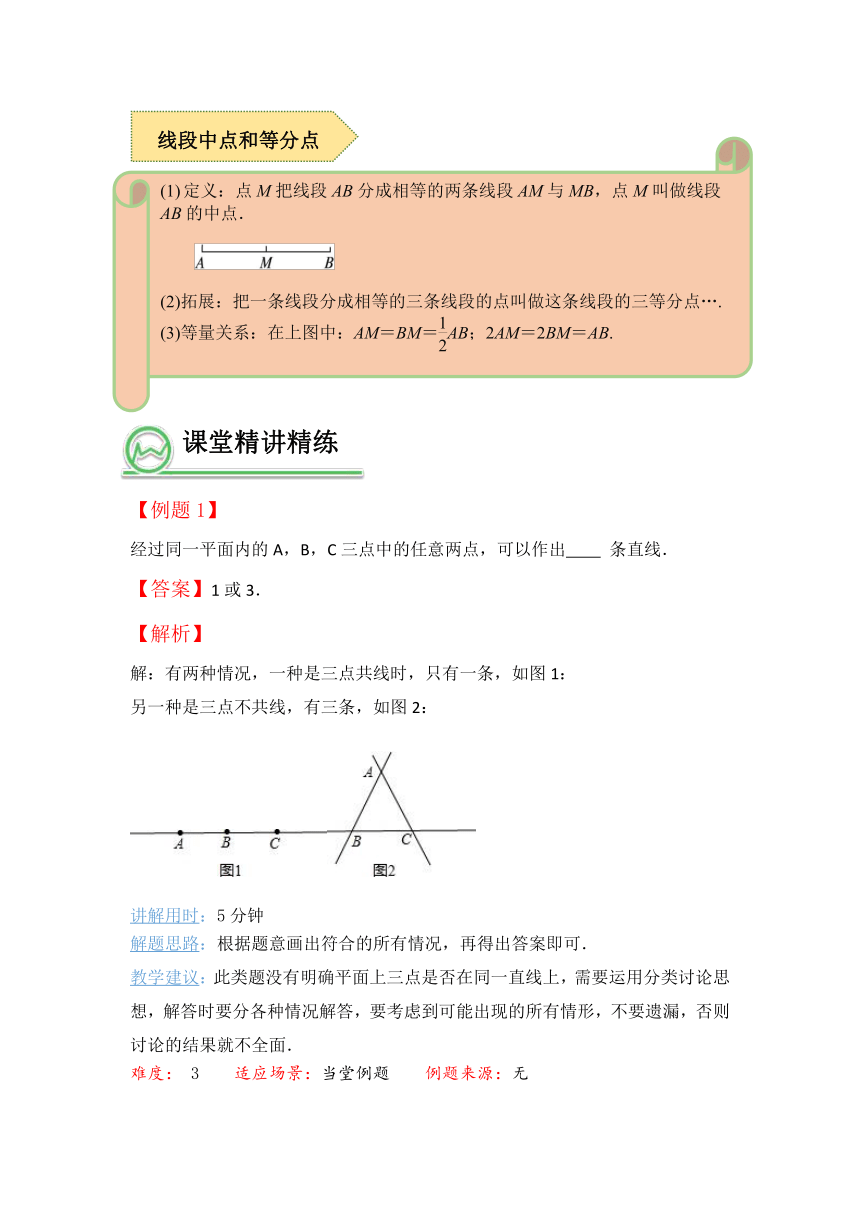
-139065301625定义:点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
(2)拓展:把一条线段分成相等的三条线段的点叫做这条线段的三等分点….
(3)等量关系:在上图中:AM=BM=AB;2AM=2BM=AB.
定义:点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
(2)拓展:把一条线段分成相等的三条线段的点叫做这条线段的三等分点….
(3)等量关系:在上图中:AM=BM=AB;2AM=2BM=AB.
1333566040线段中点和等分点
线段中点和等分点
-8572547625 课堂精讲精练
【例题1】
经过同一平面内的A,B,C三点中的任意两点,可以作出 条直线.
【答案】1或3.
【解析】
解:有两种情况,一种是三点共线时,只有一条,如图1:
另一种是三点不共线,有三条,如图2:
讲解用时:5分钟
解题思路:根据题意画出符合的所有情况,再得出答案即可.
教学建议:此类题没有明确平面上三点是否在同一直线上,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.
难度: 3 适应场景:当堂例题 例题来源:无
【练习1.1】
下列各直线的表示法中,正确的是( )
A.直线ab B.直线Ab C.直线A D.直线AB
【答案】D.
【解析】
解:根据直线的表示方法可得直线AB正确.
讲解用时:2分钟
解题思路:运用直线的表示方法判定即可.
教学建议:例题考查了直线、射线、线段,解题的关键是掌握直线表示法:用一个小写字母表示,或用两个大些字母(直线上的)表示.
难度: 3 适应场景:当堂练习 例题来源:无
【例题2】
如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有 个交点,n条直线相交最多有 个交点.
【答案】长方体、棱柱、圆锥、球、圆柱、正方体.
【解析】15;.
解:三条直线交点最多为1+2=3个,
四条直线交点最多为3+3=6个,
五条直线交点最多为6+4=10个,
六条直线交点最多为10+5=15个;
n条直线交点最多为1+2+3+…+(n﹣1)=.
故答案为:15;.
讲解用时:6分钟
解题思路:根据图形相邻两个图形的交点个数的差为从2开始的连续整数,然后列式计算即可得解;根据图形列出交点个数的算式,然后计算即可得解.
教学建议:本题是直线交点的规律题,需要引导学生观察出相邻两个图形的交点个数的差为连续整数,培养学生归纳总结的能力
难度: 3 适应场景:当堂例题 例题来源:无
【练习2.1】
观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
A.171 B.190 C.210 D.380
【答案】B.
【解析】
解:∵第一个图2条直线相交,最多有1个交点,
第二个图3条直线相交最多有3个交点,
第三个图4条直线相交,最多有6个,
而3=1+2,6=1+2+3,
∴第四个图5条直线相交,最多有1+2+3+4=10个,
∴20条直线相交,最多交点的个数是1+2+3+…+19=(1+19)×19÷2=190.
故选:B.
讲解用时:8分钟
解题思路:由于第一个图2条直线相交,最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交,最多有6个,由此得到3=1+2,6=1+2+3,那么第四个图5条直线相交,最多有1+2+3+4=10个,以此类推即可求解.
教学建议:平面内直线相交时交点个数的规律,解题时首先找出已知条件中隐含的规律,然后根据规律计算即可解决问题.
难度: 3 适应场景:当堂练习 例题来源:无
【例题3】
下列说法正确的是( )
A.射线PA和射线AP是同一条射线
B.射线OA的长度是12cm
C.直线ab、cd相交于点M
D.两点确定一条直线
【答案】D.
【解析】
解:如图
解:A、射线PA和射线AP是同一条射线,说法错误;
B、射线OA的长度是12cm,说法错误;
C、直线ab、cd相交于点M,说法错误;
D、两点确定一条直线,说法正确.
故选:D.
讲解用时:3分钟
解题思路:根据射线的表示方法判断A;根据射线的定义判断B;根据直线的表示方法判断C;根据直线的性质公理判断D.
教学建议:本题考查了直线、射线的定义及表示方法:直线可用一个小写字母表示,如:直线l,或用两个大些字母(直线上的)表示,如直线AB(或直线BA).射线是直线的一部分,可用一个小写字母表示,如:射线l;或用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.直线与射线都是无限长,不能度量.也考查了直线的性质公理.
难度: 3 适应场景:当堂练习 例题来源:无
【练习3.1】
如图所示,共有射线 条.
【答案】12.
【解析】
解:图中射线有:ED、EB、CD、CB、BE、DB、BD共7条+以E为顶点的一条+以D为顶点的两条+以B为顶点的两条,共12条,
讲解用时:5分钟
解题思路:根据直线、射线的概念进行判断即可.
教学建议:本题考查的是直线、射线的概念,正确区分直线、射线是解题的关键.
难度: 3 适应场景:当堂例题 例题来源:无
【练习3.2】
射线AB与射线BA表示同一条射线.这种说法对吗?
【答案】错误
【解析】
解:如图所示:
,
射线AB表示ABC,而射线BA表示BAD,故而得出射线AB与射线BA表示不同的射线.故这种说法错误.
讲解用时:5分钟
解题思路:根据射线的定义:直线上的一点和它一旁的部分所组成的图形称为射线,可知射线不光包括端点,也包括它一旁的部分,故可知射线AB与射线BA表示不同的射线.
教学建议:考查射线的性质,根据定义直线上的一点和它一旁的部分所组成的图形称为射线,结合图形可以比较明显的得出结论.
难度: 3 适应场景:当堂例题 例题来源:无
【例题4】
下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上;
②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是 (填序号).
【答案】②.
【解析】
解:①用两根钉子就可以把一根木条固定在墙上,根据两点确定一条直线;
②把弯曲的公路改直,就能够缩短路程,根据两点之间线段最短;
③体育课上,老师测量某个同学的跳远成绩,根据两点之间线段最短;
故答案为:②.
讲解用时:3分钟
解题思路:根据线段的性质、直线的性质分别进行分析.
教学建议:线段的性质:两点之间,线段最短.
难度: 3 适应场景:当堂例题 例题来源:无
【练习4.1】
如图:
(1)图中直线有几条?
(2)图中射线有几条?能用图中字母表示的射线有几条?你能写出来吗?
(3)图中线段有几条?你能写出来吗?
(4)如果图中有n个点,直线有几条?射线有几条?线段有几条?
【答案】(1)1条;8条,6条,分别是射线AB,射线BC,射线CD,射线DA,射线CA,射线BA.(3)6条,分别是线段AB,线段AC,线段AD,线段BC,线段BD,线段CD.(4)1条,2n条,条.
【解析】
解:(1)图中直线有1条.
(2)图中射线有8条,能用图中字母表示的射线有6条,是射线AB,射线BC,射线CD,射线DA,射线CA,射线BA.
(3)图中线段有6条,是线段AB,线段AC,线段AD,线段BC,线段BD,线段CD.
(4)如果图中有n个点,直线有1条,射线有2n条,线段有条.
讲解用时:8分钟
解题思路:(1)图中只有一条直线.(2)根据数射线的方法数出即可.(3)根据数线段的方法数出即可.(4)直线一条,射线2n条(每个点都把直线分成两条射线),根据数线段的方法得出即可.
教学建议:线段、直线、射线的应用,考查学生的理解能力和观察图形的能力.
难度: 3 适应场景:当堂练习 例题来源:无
【练习4.2】
如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
【答案】
【解析】
解:点P的位置如下图所示:
作法是:连接AB交L于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
讲解用时:5分钟
解题思路:根据线段的性质:两点之间线段最短,即可得出答案.
教学建议:考查线段的性质,注意两点之间线段最短这一知识点的灵活运用.
难度: 3 适应场景:当堂练习 例题来源:无
【例题5】
已知线段a,b,用圆规和直尺画线段,使它等于2a﹣b(简要写出画法,保留作图痕迹).
【答案】
【解析】
解:如图所示:
首先画射线,再在射线上依次截取AB=BC=a,然后再截取AD=b,
则CD=2a﹣b.
讲解用时:5分钟
解题思路:首先画出射线,然后再在射线上截取线段AB=BC=a,截取AD=b,可得CD=2a﹣b.
教学建议:要求学生学会如何在射线上截取线段等于已知线段.
难度: 3 适应场景:当堂例题 例题来源:无
【练习5.1】
画图题
(1)画线段MN,使得MN=2a﹣b;
(2)在直线MN外任取一点A,画射线AM和直线AN;
(3)延长MN至点P,使AP=MA,画线段PN,试估计所画图形中PM与PN的差和线段MN的大小关系.
【答案】(1),(2)如图:
(3)PM﹣PN=MN.
【解析】
解:(1)作图如下:MN即为所求;
(2)作图如下:
(3)作图如下:由图形可知PM﹣PN=MN.
讲解用时:8分钟
解题思路:(1)①画一条直线l;②在l上任取一点M,截取MQ=2a;③在线段MQ上截取QN=b;
(2)在直线MN外任取一点A,画射线AM和直线AN即可;
(3)延长MN至点P,使AP=MA,画线段PN,再比较PM与PN的差和线段MN的大小关系.
教学建议: 考查作图﹣复杂作图和比较线段的长短,会作一条线段等于已知线段,正确理解作图要求
难度: 3 适应场景:当堂练习 例题来源:无
【练习5.2】
如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB;
(2)作射线BC;
(3)画线段CD;
(4)连接AD,并将其反向延长至E,使DE=2AD.
【答案】
【解析】
解:(1)如图所示,直线AB即为所求;
(2)如图,射线BC即为所求;
(3)如图,线段CD即为所求;
(4)如图,DE即为所求.
讲解用时:6分钟
解题思路:根据直线、射线、线段的定义作图,再利用反向延长线段进而结合DE=2AD得出答案.
教学建议: 掌握直线、射线、线段的定义及性质
难度: 3 适应场景:当堂练习 例题来源:无
【例题6】
如图,若CB=4cm,DB=7cm,且D是AC的中点,求AC的长.
【答案】6cm.
【解析】
解:CD=DB﹣BC=7﹣4=3cm,
AC=2CD=2×3=6cm.
讲解用时:5分钟
解题思路:理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系进行解题.
教学建议:掌握灵活运用线段的和、差、倍、分转化线段之间的数量关系
难度: 3 适应场景:当堂例题 例题来源:无
【练习6.1】
如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】
2638425254635解:如图,若B是线段AC的中点,
则AB=AC,AB=BC,AC=2AB,
而AB+BC=AC,B可是线段AC上的任意一点,
∴表示B是线段AC的中点的有①②③3个.
故选:C.
讲解用时:5分钟
解题思路:根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
教学建议:利用中点性质转化线段之间的倍分关系,在不同的情况下灵活选用它的不同表示方法
难度: 3 适应场景:当堂练习 例题来源:无
【练习6.2】
若点B在线段AC上,AB=6cm,BC=10cm,P、Q分别是AB、BC的中点,则线段PQ的长为
【答案】8cm
【解析】
解:由分析得:PQ=PB+BQ=(AB+BC),AB=6cm,BC=10cm,所以PQ=8cm.
讲解用时:5分钟
解题思路:P、Q分别是AB、BC的中点,则PB=AB,BQ=BC,PQ=PB+BQ
=(AB+BC),AB、BC都已知,则可以求出PQ的长度.
教学建议:根据题意得出各线段长度的关系,结合已知条件即可求解.
难度: 3 适应场景:当堂练习 例题来源:无
【例题7】
在直线上取A、B、C三点,使AB=5cm,BC=3cm,点O是线段AC的中点,求线段OB的长.
【答案】1cm或4cm.
【解析】
解:分两种情况:
①如果点B在线段AC上,如图.
则OB=AB﹣OA=5cm﹣OA,
∵点O是线段AC的中点,
∴OA=(AB+BC)=4cm,
∴OB=1cm;
②如果点B在线段AC的延长线上,如图.
则OB=AB﹣OA=5cm﹣OA,
∵点O是线段AC的中点,
∴OA=(AB﹣BC)=1cm,
∴OB=4cm;
所以线段OB的长度是1cm或4cm.
讲解用时:8分钟
解题思路:此题有2种情况,作图分析:①如果点B在线段AC上,那么AB+BC=AC,又因为O是线段AC的中点,则OB=AB﹣AO;②如果点B在线段AC的延长线上OB=AB﹣OA.根据线段中点的定义分别求出OA,进而求出线段OB.
教学建议:考查了两点间的距离,线段中点的定义以及线段的计算.正确画图以及分类讨论是解题的关键.
难度: 3 适应场景:当堂例题 例题来源:无
【练习7.1】
在直线上取A,B,C三点,使得AB=9cm,BC=4cm,如果O是线段AC的中点,则线段OA的长为
【答案】2.5cm或6.5cm
【解析】
解:本题有两种情形:
(1)当点C在线段AB上时,如图.
∵AC=AB﹣BC,AB=9cm,BC=4cm,
∴AC=9﹣4=5cm.
又∵O是线段AC的中点,
∴OA=AC=2.5cm;
(2)当点C在线段AB的延长线上时,如图.
∵AC=AB+BC,AB=9cm,BC=4cm,
∴AC=9+4=13cm.
又∵O是线段AC的中点,
∴OA=AC=6.5cm.
讲解用时:6分钟
解题思路:本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意正确地画出图形解题.
教学建议:考查了两点间的距离,线段中点的定义以及线段的计算.正确画图以及分类讨论是解题的关键.
难度: 3 适应场景:当堂练习 例题来源:无
【例题8】
如图,B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,P是MN的中点,PC=2cm,求MN的长.
【答案】36cm
【解析】
解:B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,
设MB=2x,则BC=3x,CN=4x,即MP=4.5x,
故PC=MC﹣MP=5x﹣4.5x=0.5x=2cm,故x=4cm,
则MN=9x=36cm.
答:MN=36cm.
讲解用时:8分钟
解题思路:在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,根据题目中的几何图形,再根据题意进行计算.
教学建议:利用中点性质转化线段之间的倍分关系,在不同的情况下灵活选用它的不同表示方法.同时,要牢记灵活运用线段的和、差、倍、分转化线段之间的数量关系.
难度: 3 适应场景:当堂例题 例题来源:无
【练习8.1】
如图,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
【答案】8cm
【解析】
解:∵M是AC的中点,
∴MC=AM=AC=×6=3cm,
又∵CN:NB=1:2
∴CN=BC=×15=5cm,
∴MN=MC+NC=3cm+5cm=8cm.
讲解用时:6分钟
解题思路:因为点M是AC的中点,则有MC=AM=AC,又因为CN:NB=1:2,则有CN=BC,故MN=MC+NC可求.
教学建议:利用中点性质转化线段之间的倍分关系是解题的关键,本题点M是AC的中点,则有MC=AM=AC,还利用了两条线段成比例求解.
难度: 3 适应场景:当堂练习 例题来源:无
0201930
课后作业
【作业1】
下面几种表示直线的写法中,错误的是( ).
A.直线a B.直线Ma
C.直线MN D.直线MO
【答案】B.
【解析】
解:直线的表示法有两种,一种是用一个小写字母表示,另一种是用直线上两个点的大写字母表示,所以直线Ma这种表示法不正确,故选B.
讲解用时:2分钟
难度: 2 适应场景:练习题 例题来源:无
【作业2】
如图,若射线AB上有一点C,下列与射线AB是同一条射线的是( ).
A.射线BA B.射线AC
C.射线BC D.射线CB
【答案】B.
【解析】
端点相同,在同一条直线上,且方向一致,就是同一条射线,所以B正确.
讲解用时:3分钟
难度: 3 适应场景:练习题 例题来源:无
【作业3】
如图有几条直线?几条射线?几条线段?并写出.
【答案】有一条直线AB(或AC,AD,AE,BE,BD,CD,…);射线有6条:CA,CB,DA,DB,EA,EB.线段有3条:CD,CE,DE.
【解析】
解:有一条直线AB(或AC,AD,AE,BE,BD,CD,…);射线有6条:CA,CB,DA,DB,EA,EB.线段有3条:CD,CE,DE.
讲解用时:5分钟
难度: 3 适应场景:练习题 例题来源:无
【作业4】
如图,已知线段a,b,c,画一条线段,使它等于a+b-c(用尺规法).
【答案】
画法:
如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
【解析】
解:画法:如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
【作业4】
如图,已知线段a,b,c,画一条线段,使它等于a+b-c(用尺规法).
【答案】
画法:
如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
【解析】
解:画法:如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
【作业5】
线段AB=5 cm,延长AB至C,使AC=2AB,反向延长AB至E,使AE=CE,计算:(1)线段AC的长;(2)线段AE,BE的长.
【答案】(1)10cm;(2)10cm .
【解析】
解:如图:(1)因为AC=2AB,所以BC=AB=5 cm,
所以AC=AB+BC=5+5=10 (cm).
(2)因为AE=CE,所以AE=AB=BC=5 cm,
所以BE=AB+AE=5+5=10 (cm).
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
第12讲 直线、射线、线段
0329565
知识定位
讲解用时:5分钟
A、适用范围:人教版初一,基础一般;
B、知识点概述:本讲义主要用于人教版初一新课,主要学习直线、射线与线段,理解直线、射线、线段的概念,掌握它们的区别和联系;利用直线、线段的性质解决相关实际问题;利用线段的和差倍分解决相关计算问题.
0137160
知识梳理
讲解用时:15分钟
381033020直线
直线
-57151905(1)概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始的概念,直线常用“一根拉得很紧的细线”,“一张纸的折痕”等实际事物进行描述.
(2)特点:直线向两方无限延伸,不可度量,没有粗细;并且同一平面内的两条相交直线只有一个交点.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.即“两点确定一条直线”.
(4)直线的两种表示法:一是用一个小写字母表示:如直线a,b,c或直线l等.另一个是用直线上两个点的大写字母表示,如:直线AB或直线BA.如图:表示为直线l或直线AB(点的字母位置可以交换).
(5)直线与点的位置关系:一是点在直线上,也叫做直线经过这点;另一种是点在直线外,也叫做直线不经过这个点.
(1)概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始的概念,直线常用“一根拉得很紧的细线”,“一张纸的折痕”等实际事物进行描述.
(2)特点:直线向两方无限延伸,不可度量,没有粗细;并且同一平面内的两条相交直线只有一个交点.
(3)直线的基本性质:经过两点有一条直线,并且只有一条直线.即“两点确定一条直线”.
(4)直线的两种表示法:一是用一个小写字母表示:如直线a,b,c或直线l等.另一个是用直线上两个点的大写字母表示,如:直线AB或直线BA.如图:表示为直线l或直线AB(点的字母位置可以交换).
(5)直线与点的位置关系:一是点在直线上,也叫做直线经过这点;另一种是点在直线外,也叫做直线不经过这个点.
3810143510射线
射线
13335118745(1)定义:直线上一点和它一旁的部分,叫做射线.它是直线的一部分.如图就是一条射线,其中O是射线的端点.
(2)表示法:同直线一样,射线也有两种表示方法,一种是用一个小写字母表示:如射线a,b,c或射线l等,另一个是用射线上两个点的大写字母表示,其中前面的字母表示的点必须是端点.如图:表示为射线l或射线OA.
注意:表示射线端点的字母一定要写在前面.
(3)特点:射线只有1个端点,向一方无限延伸,因此不可度量.
(1)定义:直线上一点和它一旁的部分,叫做射线.它是直线的一部分.如图就是一条射线,其中O是射线的端点.
(2)表示法:同直线一样,射线也有两种表示方法,一种是用一个小写字母表示:如射线a,b,c或射线l等,另一个是用射线上两个点的大写字母表示,其中前面的字母表示的点必须是端点.如图:表示为射线l或射线OA.
注意:表示射线端点的字母一定要写在前面.
(3)特点:射线只有1个端点,向一方无限延伸,因此不可度量.
-139065107315(1)定义:直线上两点和它们之间的部分,叫做线段.它是直线的一部分.
(2)特点:有两个端点,不能向两方无限延伸,因此它有长度,有大小.
(3)表示法:同直线一样,线段也有两种表示法,一种是用一个小写字母表示,如线段a,b,c.另一种是用线段两个端点的大写字母表示.如图:可以表示为:线段AB或线段BA,或线段a.
(4)线段的基本性质:两点的所有连线中,线段最短,简单的说成:“两点之间,线段最短.”意义:选取最短路线的原则和依据.
(5)两点间的距离:连接两点的线段的长度,叫做这两点间的距离.
注意 线段的表示 表示线段的两端点的字母可以交换,如线段AB也是线段BA,但端点字母不同线段就不一样.
(1)定义:直线上两点和它们之间的部分,叫做线段.它是直线的一部分.
(2)特点:有两个端点,不能向两方无限延伸,因此它有长度,有大小.
(3)表示法:同直线一样,线段也有两种表示法,一种是用一个小写字母表示,如线段a,b,c.另一种是用线段两个端点的大写字母表示.如图:可以表示为:线段AB或线段BA,或线段a.
(4)线段的基本性质:两点的所有连线中,线段最短,简单的说成:“两点之间,线段最短.”意义:选取最短路线的原则和依据.
(5)两点间的距离:连接两点的线段的长度,叫做这两点间的距离.
注意 线段的表示 表示线段的两端点的字母可以交换,如线段AB也是线段BA,但端点字母不同线段就不一样.
-34290112395线段
线段
1333566040线段的画法
线段的画法
-5715213995(1)画一条线段等于已知线段
画法:①测量法:用刻度尺先量出已知线段的长度,画一条等于这个长度的线段;
②尺规法:如图:画一条射线AB,在这条射线上截取(用圆规)
AC=a.
(2)画线段的和差
测量法:量出每一条线段的长度,求出它们的和差,画一条线段等于计算结果的长度.如:已知线段a,b(a>b),画线段AB=a-b,就是计算出a-b的长度,画出线段AB等于a-b的长度即可.
尺规法:如图,已知线段a,b,画一条线段,使它等于2b-a.
画法:如图,①画一条射线AB,在这条射线上连续截取(用圆规)AC=2b,
②再以A为一个端点,截取AD=a,那么DC=2b-a.
(1)画一条线段等于已知线段
画法:①测量法:用刻度尺先量出已知线段的长度,画一条等于这个长度的线段;
②尺规法:如图:画一条射线AB,在这条射线上截取(用圆规)
AC=a.
(2)画线段的和差
测量法:量出每一条线段的长度,求出它们的和差,画一条线段等于计算结果的长度.如:已知线段a,b(a>b),画线段AB=a-b,就是计算出a-b的长度,画出线段AB等于a-b的长度即可.
尺规法:如图,已知线段a,b,画一条线段,使它等于2b-a.
画法:如图,①画一条射线AB,在这条射线上连续截取(用圆规)AC=2b,
②再以A为一个端点,截取AD=a,那么DC=2b-a.
-3429025400线段的比较
线段的比较
-53340172085(1)测量法:就是用刻度尺测量出两条线段的长度,再比较它们的大小.
(2)叠合法:把两条线段的一端对齐,放在一起进行比较.如图:
①若C点落在线段AB内,那么AB>AC;
②若C点落在线段AB的一个端点上,那么AB=AC;
③若C点落在线段AB外(准确的说是AB的延长线上),那么AB<AC.
谈重点 线段的比较 用叠合法比较两条线段的大小,一端一定要对齐,看另一个端点的落点,测量法要注意单位的统一.
(1)测量法:就是用刻度尺测量出两条线段的长度,再比较它们的大小.
(2)叠合法:把两条线段的一端对齐,放在一起进行比较.如图:
①若C点落在线段AB内,那么AB>AC;
②若C点落在线段AB的一个端点上,那么AB=AC;
③若C点落在线段AB外(准确的说是AB的延长线上),那么AB<AC.
谈重点 线段的比较 用叠合法比较两条线段的大小,一端一定要对齐,看另一个端点的落点,测量法要注意单位的统一.
-139065301625定义:点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
(2)拓展:把一条线段分成相等的三条线段的点叫做这条线段的三等分点….
(3)等量关系:在上图中:AM=BM=AB;2AM=2BM=AB.
定义:点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.
(2)拓展:把一条线段分成相等的三条线段的点叫做这条线段的三等分点….
(3)等量关系:在上图中:AM=BM=AB;2AM=2BM=AB.
1333566040线段中点和等分点
线段中点和等分点
-8572547625 课堂精讲精练
【例题1】
经过同一平面内的A,B,C三点中的任意两点,可以作出 条直线.
【答案】1或3.
【解析】
解:有两种情况,一种是三点共线时,只有一条,如图1:
另一种是三点不共线,有三条,如图2:
讲解用时:5分钟
解题思路:根据题意画出符合的所有情况,再得出答案即可.
教学建议:此类题没有明确平面上三点是否在同一直线上,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.
难度: 3 适应场景:当堂例题 例题来源:无
【练习1.1】
下列各直线的表示法中,正确的是( )
A.直线ab B.直线Ab C.直线A D.直线AB
【答案】D.
【解析】
解:根据直线的表示方法可得直线AB正确.
讲解用时:2分钟
解题思路:运用直线的表示方法判定即可.
教学建议:例题考查了直线、射线、线段,解题的关键是掌握直线表示法:用一个小写字母表示,或用两个大些字母(直线上的)表示.
难度: 3 适应场景:当堂练习 例题来源:无
【例题2】
如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有 个交点,n条直线相交最多有 个交点.
【答案】长方体、棱柱、圆锥、球、圆柱、正方体.
【解析】15;.
解:三条直线交点最多为1+2=3个,
四条直线交点最多为3+3=6个,
五条直线交点最多为6+4=10个,
六条直线交点最多为10+5=15个;
n条直线交点最多为1+2+3+…+(n﹣1)=.
故答案为:15;.
讲解用时:6分钟
解题思路:根据图形相邻两个图形的交点个数的差为从2开始的连续整数,然后列式计算即可得解;根据图形列出交点个数的算式,然后计算即可得解.
教学建议:本题是直线交点的规律题,需要引导学生观察出相邻两个图形的交点个数的差为连续整数,培养学生归纳总结的能力
难度: 3 适应场景:当堂例题 例题来源:无
【练习2.1】
观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
A.171 B.190 C.210 D.380
【答案】B.
【解析】
解:∵第一个图2条直线相交,最多有1个交点,
第二个图3条直线相交最多有3个交点,
第三个图4条直线相交,最多有6个,
而3=1+2,6=1+2+3,
∴第四个图5条直线相交,最多有1+2+3+4=10个,
∴20条直线相交,最多交点的个数是1+2+3+…+19=(1+19)×19÷2=190.
故选:B.
讲解用时:8分钟
解题思路:由于第一个图2条直线相交,最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交,最多有6个,由此得到3=1+2,6=1+2+3,那么第四个图5条直线相交,最多有1+2+3+4=10个,以此类推即可求解.
教学建议:平面内直线相交时交点个数的规律,解题时首先找出已知条件中隐含的规律,然后根据规律计算即可解决问题.
难度: 3 适应场景:当堂练习 例题来源:无
【例题3】
下列说法正确的是( )
A.射线PA和射线AP是同一条射线
B.射线OA的长度是12cm
C.直线ab、cd相交于点M
D.两点确定一条直线
【答案】D.
【解析】
解:如图
解:A、射线PA和射线AP是同一条射线,说法错误;
B、射线OA的长度是12cm,说法错误;
C、直线ab、cd相交于点M,说法错误;
D、两点确定一条直线,说法正确.
故选:D.
讲解用时:3分钟
解题思路:根据射线的表示方法判断A;根据射线的定义判断B;根据直线的表示方法判断C;根据直线的性质公理判断D.
教学建议:本题考查了直线、射线的定义及表示方法:直线可用一个小写字母表示,如:直线l,或用两个大些字母(直线上的)表示,如直线AB(或直线BA).射线是直线的一部分,可用一个小写字母表示,如:射线l;或用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.直线与射线都是无限长,不能度量.也考查了直线的性质公理.
难度: 3 适应场景:当堂练习 例题来源:无
【练习3.1】
如图所示,共有射线 条.
【答案】12.
【解析】
解:图中射线有:ED、EB、CD、CB、BE、DB、BD共7条+以E为顶点的一条+以D为顶点的两条+以B为顶点的两条,共12条,
讲解用时:5分钟
解题思路:根据直线、射线的概念进行判断即可.
教学建议:本题考查的是直线、射线的概念,正确区分直线、射线是解题的关键.
难度: 3 适应场景:当堂例题 例题来源:无
【练习3.2】
射线AB与射线BA表示同一条射线.这种说法对吗?
【答案】错误
【解析】
解:如图所示:
,
射线AB表示ABC,而射线BA表示BAD,故而得出射线AB与射线BA表示不同的射线.故这种说法错误.
讲解用时:5分钟
解题思路:根据射线的定义:直线上的一点和它一旁的部分所组成的图形称为射线,可知射线不光包括端点,也包括它一旁的部分,故可知射线AB与射线BA表示不同的射线.
教学建议:考查射线的性质,根据定义直线上的一点和它一旁的部分所组成的图形称为射线,结合图形可以比较明显的得出结论.
难度: 3 适应场景:当堂例题 例题来源:无
【例题4】
下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上;
②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是 (填序号).
【答案】②.
【解析】
解:①用两根钉子就可以把一根木条固定在墙上,根据两点确定一条直线;
②把弯曲的公路改直,就能够缩短路程,根据两点之间线段最短;
③体育课上,老师测量某个同学的跳远成绩,根据两点之间线段最短;
故答案为:②.
讲解用时:3分钟
解题思路:根据线段的性质、直线的性质分别进行分析.
教学建议:线段的性质:两点之间,线段最短.
难度: 3 适应场景:当堂例题 例题来源:无
【练习4.1】
如图:
(1)图中直线有几条?
(2)图中射线有几条?能用图中字母表示的射线有几条?你能写出来吗?
(3)图中线段有几条?你能写出来吗?
(4)如果图中有n个点,直线有几条?射线有几条?线段有几条?
【答案】(1)1条;8条,6条,分别是射线AB,射线BC,射线CD,射线DA,射线CA,射线BA.(3)6条,分别是线段AB,线段AC,线段AD,线段BC,线段BD,线段CD.(4)1条,2n条,条.
【解析】
解:(1)图中直线有1条.
(2)图中射线有8条,能用图中字母表示的射线有6条,是射线AB,射线BC,射线CD,射线DA,射线CA,射线BA.
(3)图中线段有6条,是线段AB,线段AC,线段AD,线段BC,线段BD,线段CD.
(4)如果图中有n个点,直线有1条,射线有2n条,线段有条.
讲解用时:8分钟
解题思路:(1)图中只有一条直线.(2)根据数射线的方法数出即可.(3)根据数线段的方法数出即可.(4)直线一条,射线2n条(每个点都把直线分成两条射线),根据数线段的方法得出即可.
教学建议:线段、直线、射线的应用,考查学生的理解能力和观察图形的能力.
难度: 3 适应场景:当堂练习 例题来源:无
【练习4.2】
如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
【答案】
【解析】
解:点P的位置如下图所示:
作法是:连接AB交L于点P,则P点为汽车站位置,
理由是:两点之间,线段最短.
讲解用时:5分钟
解题思路:根据线段的性质:两点之间线段最短,即可得出答案.
教学建议:考查线段的性质,注意两点之间线段最短这一知识点的灵活运用.
难度: 3 适应场景:当堂练习 例题来源:无
【例题5】
已知线段a,b,用圆规和直尺画线段,使它等于2a﹣b(简要写出画法,保留作图痕迹).
【答案】
【解析】
解:如图所示:
首先画射线,再在射线上依次截取AB=BC=a,然后再截取AD=b,
则CD=2a﹣b.
讲解用时:5分钟
解题思路:首先画出射线,然后再在射线上截取线段AB=BC=a,截取AD=b,可得CD=2a﹣b.
教学建议:要求学生学会如何在射线上截取线段等于已知线段.
难度: 3 适应场景:当堂例题 例题来源:无
【练习5.1】
画图题
(1)画线段MN,使得MN=2a﹣b;
(2)在直线MN外任取一点A,画射线AM和直线AN;
(3)延长MN至点P,使AP=MA,画线段PN,试估计所画图形中PM与PN的差和线段MN的大小关系.
【答案】(1),(2)如图:
(3)PM﹣PN=MN.
【解析】
解:(1)作图如下:MN即为所求;
(2)作图如下:
(3)作图如下:由图形可知PM﹣PN=MN.
讲解用时:8分钟
解题思路:(1)①画一条直线l;②在l上任取一点M,截取MQ=2a;③在线段MQ上截取QN=b;
(2)在直线MN外任取一点A,画射线AM和直线AN即可;
(3)延长MN至点P,使AP=MA,画线段PN,再比较PM与PN的差和线段MN的大小关系.
教学建议: 考查作图﹣复杂作图和比较线段的长短,会作一条线段等于已知线段,正确理解作图要求
难度: 3 适应场景:当堂练习 例题来源:无
【练习5.2】
如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB;
(2)作射线BC;
(3)画线段CD;
(4)连接AD,并将其反向延长至E,使DE=2AD.
【答案】
【解析】
解:(1)如图所示,直线AB即为所求;
(2)如图,射线BC即为所求;
(3)如图,线段CD即为所求;
(4)如图,DE即为所求.
讲解用时:6分钟
解题思路:根据直线、射线、线段的定义作图,再利用反向延长线段进而结合DE=2AD得出答案.
教学建议: 掌握直线、射线、线段的定义及性质
难度: 3 适应场景:当堂练习 例题来源:无
【例题6】
如图,若CB=4cm,DB=7cm,且D是AC的中点,求AC的长.
【答案】6cm.
【解析】
解:CD=DB﹣BC=7﹣4=3cm,
AC=2CD=2×3=6cm.
讲解用时:5分钟
解题思路:理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系进行解题.
教学建议:掌握灵活运用线段的和、差、倍、分转化线段之间的数量关系
难度: 3 适应场景:当堂例题 例题来源:无
【练习6.1】
如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( )
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】
2638425254635解:如图,若B是线段AC的中点,
则AB=AC,AB=BC,AC=2AB,
而AB+BC=AC,B可是线段AC上的任意一点,
∴表示B是线段AC的中点的有①②③3个.
故选:C.
讲解用时:5分钟
解题思路:根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
教学建议:利用中点性质转化线段之间的倍分关系,在不同的情况下灵活选用它的不同表示方法
难度: 3 适应场景:当堂练习 例题来源:无
【练习6.2】
若点B在线段AC上,AB=6cm,BC=10cm,P、Q分别是AB、BC的中点,则线段PQ的长为
【答案】8cm
【解析】
解:由分析得:PQ=PB+BQ=(AB+BC),AB=6cm,BC=10cm,所以PQ=8cm.
讲解用时:5分钟
解题思路:P、Q分别是AB、BC的中点,则PB=AB,BQ=BC,PQ=PB+BQ
=(AB+BC),AB、BC都已知,则可以求出PQ的长度.
教学建议:根据题意得出各线段长度的关系,结合已知条件即可求解.
难度: 3 适应场景:当堂练习 例题来源:无
【例题7】
在直线上取A、B、C三点,使AB=5cm,BC=3cm,点O是线段AC的中点,求线段OB的长.
【答案】1cm或4cm.
【解析】
解:分两种情况:
①如果点B在线段AC上,如图.
则OB=AB﹣OA=5cm﹣OA,
∵点O是线段AC的中点,
∴OA=(AB+BC)=4cm,
∴OB=1cm;
②如果点B在线段AC的延长线上,如图.
则OB=AB﹣OA=5cm﹣OA,
∵点O是线段AC的中点,
∴OA=(AB﹣BC)=1cm,
∴OB=4cm;
所以线段OB的长度是1cm或4cm.
讲解用时:8分钟
解题思路:此题有2种情况,作图分析:①如果点B在线段AC上,那么AB+BC=AC,又因为O是线段AC的中点,则OB=AB﹣AO;②如果点B在线段AC的延长线上OB=AB﹣OA.根据线段中点的定义分别求出OA,进而求出线段OB.
教学建议:考查了两点间的距离,线段中点的定义以及线段的计算.正确画图以及分类讨论是解题的关键.
难度: 3 适应场景:当堂例题 例题来源:无
【练习7.1】
在直线上取A,B,C三点,使得AB=9cm,BC=4cm,如果O是线段AC的中点,则线段OA的长为
【答案】2.5cm或6.5cm
【解析】
解:本题有两种情形:
(1)当点C在线段AB上时,如图.
∵AC=AB﹣BC,AB=9cm,BC=4cm,
∴AC=9﹣4=5cm.
又∵O是线段AC的中点,
∴OA=AC=2.5cm;
(2)当点C在线段AB的延长线上时,如图.
∵AC=AB+BC,AB=9cm,BC=4cm,
∴AC=9+4=13cm.
又∵O是线段AC的中点,
∴OA=AC=6.5cm.
讲解用时:6分钟
解题思路:本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意正确地画出图形解题.
教学建议:考查了两点间的距离,线段中点的定义以及线段的计算.正确画图以及分类讨论是解题的关键.
难度: 3 适应场景:当堂练习 例题来源:无
【例题8】
如图,B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,P是MN的中点,PC=2cm,求MN的长.
【答案】36cm
【解析】
解:B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,
设MB=2x,则BC=3x,CN=4x,即MP=4.5x,
故PC=MC﹣MP=5x﹣4.5x=0.5x=2cm,故x=4cm,
则MN=9x=36cm.
答:MN=36cm.
讲解用时:8分钟
解题思路:在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,根据题目中的几何图形,再根据题意进行计算.
教学建议:利用中点性质转化线段之间的倍分关系,在不同的情况下灵活选用它的不同表示方法.同时,要牢记灵活运用线段的和、差、倍、分转化线段之间的数量关系.
难度: 3 适应场景:当堂例题 例题来源:无
【练习8.1】
如图,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
【答案】8cm
【解析】
解:∵M是AC的中点,
∴MC=AM=AC=×6=3cm,
又∵CN:NB=1:2
∴CN=BC=×15=5cm,
∴MN=MC+NC=3cm+5cm=8cm.
讲解用时:6分钟
解题思路:因为点M是AC的中点,则有MC=AM=AC,又因为CN:NB=1:2,则有CN=BC,故MN=MC+NC可求.
教学建议:利用中点性质转化线段之间的倍分关系是解题的关键,本题点M是AC的中点,则有MC=AM=AC,还利用了两条线段成比例求解.
难度: 3 适应场景:当堂练习 例题来源:无
0201930
课后作业
【作业1】
下面几种表示直线的写法中,错误的是( ).
A.直线a B.直线Ma
C.直线MN D.直线MO
【答案】B.
【解析】
解:直线的表示法有两种,一种是用一个小写字母表示,另一种是用直线上两个点的大写字母表示,所以直线Ma这种表示法不正确,故选B.
讲解用时:2分钟
难度: 2 适应场景:练习题 例题来源:无
【作业2】
如图,若射线AB上有一点C,下列与射线AB是同一条射线的是( ).
A.射线BA B.射线AC
C.射线BC D.射线CB
【答案】B.
【解析】
端点相同,在同一条直线上,且方向一致,就是同一条射线,所以B正确.
讲解用时:3分钟
难度: 3 适应场景:练习题 例题来源:无
【作业3】
如图有几条直线?几条射线?几条线段?并写出.
【答案】有一条直线AB(或AC,AD,AE,BE,BD,CD,…);射线有6条:CA,CB,DA,DB,EA,EB.线段有3条:CD,CE,DE.
【解析】
解:有一条直线AB(或AC,AD,AE,BE,BD,CD,…);射线有6条:CA,CB,DA,DB,EA,EB.线段有3条:CD,CE,DE.
讲解用时:5分钟
难度: 3 适应场景:练习题 例题来源:无
【作业4】
如图,已知线段a,b,c,画一条线段,使它等于a+b-c(用尺规法).
【答案】
画法:
如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
【解析】
解:画法:如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
【作业4】
如图,已知线段a,b,c,画一条线段,使它等于a+b-c(用尺规法).
【答案】
画法:
如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
【解析】
解:画法:如图,①画射线(直线也可)AB,在射线AB上分别截取AC=a,CD=b.
②以D为一个端点在AD上截取DE=c,线段AE即为所求.
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
【作业5】
线段AB=5 cm,延长AB至C,使AC=2AB,反向延长AB至E,使AE=CE,计算:(1)线段AC的长;(2)线段AE,BE的长.
【答案】(1)10cm;(2)10cm .
【解析】
解:如图:(1)因为AC=2AB,所以BC=AB=5 cm,
所以AC=AB+BC=5+5=10 (cm).
(2)因为AE=CE,所以AE=AB=BC=5 cm,
所以BE=AB+AE=5+5=10 (cm).
讲解用时:4分钟
难度: 3 适应场景:练习题 例题来源:无
