北师大版九年级数学上册 1.1菱形的性质和判定 同步练习题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册 1.1菱形的性质和判定 同步练习题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:03:05 | ||
图片预览

文档简介
北师大版九年级数学上册第一章
1.1菱形的性质和判定
同步练习题
一、选择题
1.下列命题中正确的是( )
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
2.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
3.如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,若AE=4
cm,那么四边形AEDF的周长为( )
A.12
cm
B.16
cm
C.20
cm
D.22
cm
4.如图,将?
ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF
B.AB=EF
C.AE=AF
D.AF=BE
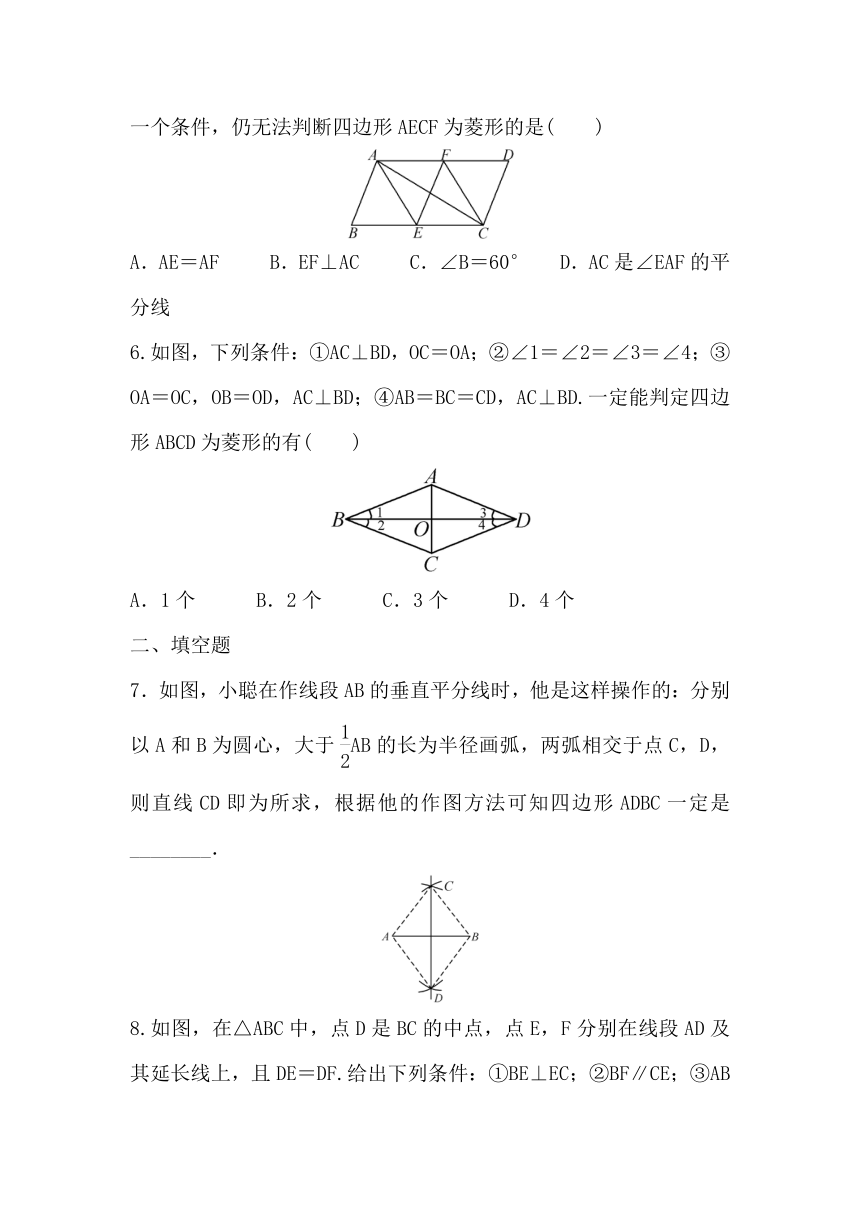
5.如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF
B.EF⊥AC
C.∠B=60°
D.AC是∠EAF的平分线
6.如图,下列条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.一定能判定四边形ABCD为菱形的有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
7.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求,根据他的作图方法可知四边形ADBC一定是________.
8.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是________.
(只填写序号)
9.如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:
①AB∥CD;②AC⊥BD;③AO=OC;④四边形ABCD是菱形,其中正确的结论有______.(只填序号即可)
三、解答题
10.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,分别与BC,CD交于点E,F,EH⊥AB于点H,连接FH,求证:四边形CFHE是菱形.
11.如图,在四边形ABCD中,AB∥CD,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)判断四边形ABCD是什么特殊四边形?并说明理由;
(2)试确定E点的位置,使∠EFD=∠BCD,并说明理由.
12.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AEF按如图①所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
答案:
1---6
DBBCC
C
7.
菱形
8.
③
9.
①②③④
10.
∵∠ACB=90°,AE平分∠BAC,EH⊥AB,∴CE=EH.在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,∴Rt△ACE≌Rt△AHE,∴AC=AH,∵AE平分∠CAB,∴∠CAF=∠HAF,∴△CAF≌△HAF(SAS),∴∠ACD=∠AHF,可证∠ACD=∠B=∠AHF,∴FH∥CE,易证CF∥EH,
∴四边形CFHE是平行四边形,又∵CE=HE,∴平行四边形CFHE是菱形.
11.
(1)四边形ABCD是菱形.理由如下:∵AB∥CD,∴∠BAC=∠ACD,∵AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC,∴∠ACB=∠ACD,∴∠BAC=∠ACB,∴AB=BC=CD=AD,∴四边形ABCD是菱形.
(2)当BE⊥CD时,∠EFD=∠BCD.理由如下:易证△CBF≌△CDF,∴∠CBF=∠CDF,又∵BE⊥CD,∴∠EFD+∠CDF=90°,
∠BCD+∠CBF=90°,∴∠EFD=∠BCD.
12.
(1)
证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,∴∠α=∠NAF.又∵∠B=∠F,AB=AF,∴△ABM≌△AFN,∴AM=AN.
(2)四边形ABPF是菱形.理由如下:∵∠α=30°,∠EAF=90°,
∴∠BAF=120°,又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°,∴AF∥BC,AB∥EF,∴四边形ABPF是平行四边形,又∵AB=AF,∴?ABPF是菱形.
1.1菱形的性质和判定
同步练习题
一、选择题
1.下列命题中正确的是( )
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
2.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD
3.如图,△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,若AE=4
cm,那么四边形AEDF的周长为( )
A.12
cm
B.16
cm
C.20
cm
D.22
cm
4.如图,将?
ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF
B.AB=EF
C.AE=AF
D.AF=BE
5.如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF
B.EF⊥AC
C.∠B=60°
D.AC是∠EAF的平分线
6.如图,下列条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.一定能判定四边形ABCD为菱形的有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
7.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求,根据他的作图方法可知四边形ADBC一定是________.
8.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是________.
(只填写序号)
9.如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:
①AB∥CD;②AC⊥BD;③AO=OC;④四边形ABCD是菱形,其中正确的结论有______.(只填序号即可)
三、解答题
10.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,分别与BC,CD交于点E,F,EH⊥AB于点H,连接FH,求证:四边形CFHE是菱形.
11.如图,在四边形ABCD中,AB∥CD,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)判断四边形ABCD是什么特殊四边形?并说明理由;
(2)试确定E点的位置,使∠EFD=∠BCD,并说明理由.
12.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AEF按如图①所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
答案:
1---6
DBBCC
C
7.
菱形
8.
③
9.
①②③④
10.
∵∠ACB=90°,AE平分∠BAC,EH⊥AB,∴CE=EH.在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,∴Rt△ACE≌Rt△AHE,∴AC=AH,∵AE平分∠CAB,∴∠CAF=∠HAF,∴△CAF≌△HAF(SAS),∴∠ACD=∠AHF,可证∠ACD=∠B=∠AHF,∴FH∥CE,易证CF∥EH,
∴四边形CFHE是平行四边形,又∵CE=HE,∴平行四边形CFHE是菱形.
11.
(1)四边形ABCD是菱形.理由如下:∵AB∥CD,∴∠BAC=∠ACD,∵AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC,∴∠ACB=∠ACD,∴∠BAC=∠ACB,∴AB=BC=CD=AD,∴四边形ABCD是菱形.
(2)当BE⊥CD时,∠EFD=∠BCD.理由如下:易证△CBF≌△CDF,∴∠CBF=∠CDF,又∵BE⊥CD,∴∠EFD+∠CDF=90°,
∠BCD+∠CBF=90°,∴∠EFD=∠BCD.
12.
(1)
证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,∴∠α=∠NAF.又∵∠B=∠F,AB=AF,∴△ABM≌△AFN,∴AM=AN.
(2)四边形ABPF是菱形.理由如下:∵∠α=30°,∠EAF=90°,
∴∠BAF=120°,又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°,∴AF∥BC,AB∥EF,∴四边形ABPF是平行四边形,又∵AB=AF,∴?ABPF是菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
