人教版高二物理选修3-2第四章 法拉第电磁感应定律课件(共27张PPT)
文档属性
| 名称 | 人教版高二物理选修3-2第四章 法拉第电磁感应定律课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
法拉第电磁感应定律
电磁感应规律综合应用的四种题型
2、电磁感应中的力学问题
1、电磁感应中的电路问题
3、电磁感应中的能量问题
4、电磁感应中的图象问题
1、电磁感应中的电路问题
如图所示,一个500匝的线圈的两端跟R=99Ω的电阻相连接,置于竖直向下的匀强磁场中,线圈的横截面积是20㎝2,电阻为1Ω,磁场的磁感应强度随时间变化的图象如图所示。求磁场变化过程中通过电阻R的电流为多大?
解析:由图b知,线圈中磁感应强度B均匀增加,其变
化率ΔB/Δt=(50-10)/4=10T/s.
1、电磁感应中的电路问题
基本方法:
1、用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向。
2、画等效电路。
3、运用闭合电路欧姆定律,串并联电路性质,电功率等公式联立求解。
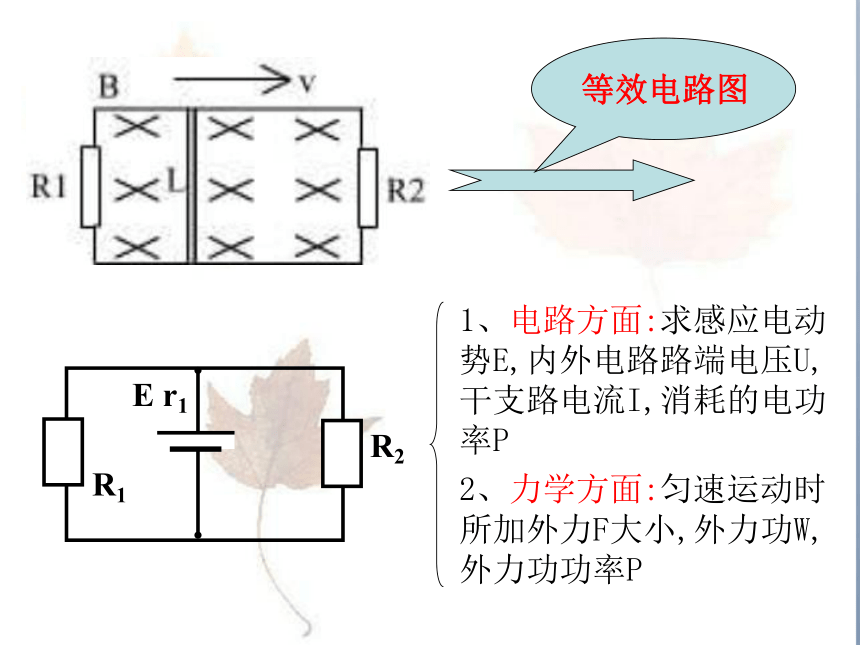
等效电路图
1、电路方面:求感应电动势E,内外电路路端电压U,干支路电流I,消耗的电功率P
2、力学方面:匀速运动时所加外力F大小,外力功W,外力功功率P
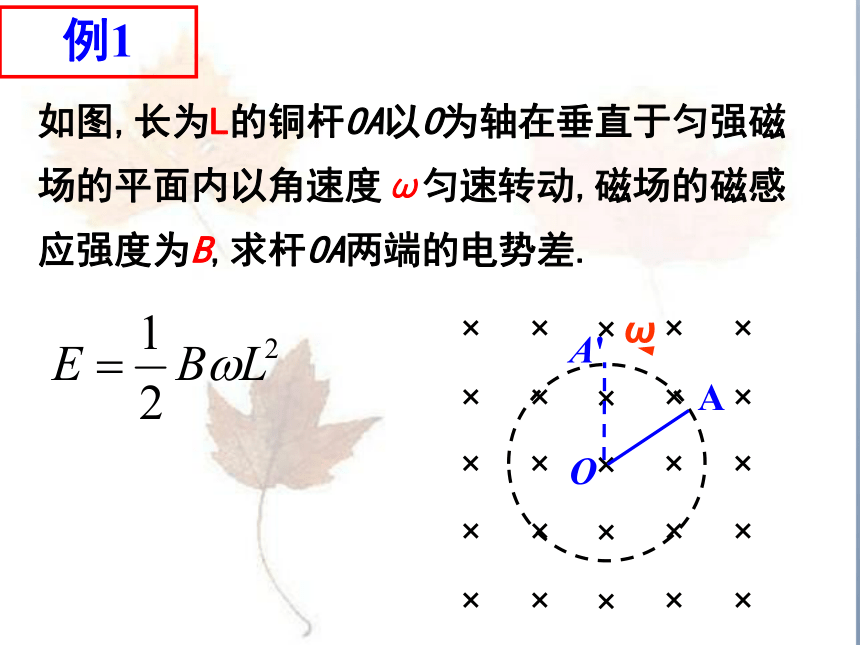
如图,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA两端的电势差.
例1
如图,有一匀强磁场B=1.0×10-3T,在垂直磁场的平面内,有一金属棒AO,绕平行于磁场的O轴顺时针转动,已知棒长L=0.20m,角速度ω=20rad/s,求:棒产生的感应电动势有多大?
练习1
如图所示,在磁感应强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架。OC为一端绕O点在框架上滑动的导体棒,OA之间连一个阻值为R的电阻(其余电阻都不计),若使OC以角速度ω匀速转动。试求:
(1)图中哪部分相当于电源?
(2)感应电动势E为多少?
(3)流过电阻R的电流I为多少?
练习2
(1)导体棒OC
(2)
(3)
3、把总电阻为2R的均匀电阻丝焊接成一半径为a的圆环,水平固定在竖直向下的磁感应强度为B的匀强磁场中,如图所示,一长度为2a,电阻为R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的接触,当金属棒以恒定速度v向右移动经过环心O时,求:
2、在圆环和金属棒上消耗的总功率
1、棒上的电流I大小,棒两端的电压U
4、如图所示,电阻不计的裸导体AB与宽为60cm的平行金属导轨良好接触,电阻R1=3Ω,
R2=6Ω,整个装置处在垂直导轨向里的匀强磁场中,磁感应强度B=0.5T。当AB向右以V=5m/s的速度匀速滑动时,求流过电阻R1、
R2的电流大小。
2、电磁感应中的力学问题
电磁感应中产生的感应电流在磁场中将受到安培力的作用,因此,电磁感应问题往往跟力学问题联系在一起,解决这类电磁感应中的力学问题,不仅要应用电磁学中的有关规律,如楞次定律、法拉第电磁感应定律、左右手定则、安培力的计算公式等,还要应用力学中的有关规律,如牛顿运动定律、动能定理、机械能守恒定律等。要将电磁学和力学的知识综合起来应用。
由于安培力和导体中的电流、运动速度均有关,
所以对磁场中运动导体进行动态分析十分必要。
【例1】水平放置于匀强磁场中的光滑导轨上,有一根导体棒ab,用恒力F作用在ab上,由静止开始运动,回路总电阻为R,分析ab
的运动情况,并求ab的最大速度。
a=(F-f)/m
v
E=BLv
I=
E/R
f=BIL
解:当f=F
时,a=0,速度达到最大,
F=f=BIL=B2
L2
vm
/R
vm=FR
/
B2
L2
vm称为收尾速度.
2、电磁感应中的力学问题
2、电磁感应中的力学问题
基本方法:
1、用法拉第电磁感应定律和楞次定律
求感应电动势的大小和方向。
2、求回路中的电流强度
3、分析导体受力情况(包含安培力,用左手定则)
4、列动力学方程求解。
【例2】
在磁感应强度为B的水平均强磁场中,竖直放置一个冂形金属框ABCD,框面垂直于磁场,宽度BC=L
,质量m的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为R,当杆自静止开始沿框架下滑时:
(1)开始下滑的加速度为多少?
(2)框内感应电流的方向怎样?安培力的方向?
(3)金属杆下滑的最大速度是多少?
解:(1)开始PQ受力为mg,
所以
a=g
(2)PQ向下加速运动,产生感应电流,方向顺时针,受到向上的磁场力F作用。
(3)达最大速度时,
F=BIL=B2
L2
vm
/R=mg
∴vm=mgR
/
B2
L2
【例3】已知:AB、CD足够长,L,θ,B,R。金属棒ab垂直于导轨放置,与导轨间的动摩擦因数为μ,质量为m,从静止开始沿导轨下滑,导轨和金属棒的电阻阻都不计。求ab棒下滑的最大速度
速度最大时做匀速运动
受力分析,列动力学方程
(1)金属杆刚进入磁场时的感应电动势;
(2)金属杆刚进入磁场时的加速度;
①感应电动势的大小
②感应电流的大小和方向
③使金属棒匀速运动所需的拉力
④感应电流的功率
⑤拉力的功率
【作业1】如图B=2T,金属棒ab向右匀速运动,v=5m/s,L=40cm,电阻R=2Ω,其余电阻不计,摩擦也不计,试求:
【作业2】宽1m,足够长的冂形金属框架竖直放置,一根质量是0.1kg,电阻0.1Ω的金属杆可沿框架无摩擦地滑动.金属杆MN下方0.8m处有一垂直框架平面的匀强磁场,磁感应强度是0.1T,金属杆MN由静止释放(如图).求:
【作业1】竖直放置冂形金属框架,宽1m,足够长,一根质量是0.1kg,电阻0.1Ω的金属杆可沿框架无摩擦地滑动.框架下部有一垂直框架平面的匀强磁场,磁感应强度是0.1T,金属杆MN自磁场边界上方0.8m处由静止释放(如图).求:
(1)金属杆刚进入磁场时的感应电动势;
(2)金属杆刚进入磁场时的加速度;
答:(1)
(2)
I=E/R=4A
F=BIL=0.4N
a=(mg-F)/m=6m/s2;
E=BLv=0.4V;
【作业2】如图B=2T,金属棒ab向右匀速运动,v=5m/s,
L=40cm,电阻R=2Ω,其余电阻不计,摩擦也不计,试
求:①感应电动势的大小
②感应电流的大小和方向
③使金属棒匀速运动所需的拉力
④感应电流的功率
⑤拉力的功率
右手定则
①
4v;
②
2A,b-a;
③
1.6N;
④
8w;
④
8w
3、电磁感应中的能量问题
4、电磁感应中的图象问题
能量转化特点:①导体切割磁感线或磁通量发生变化在回路中产生感应电流,机械能或其他形式的能量便转化为电能。
②具有感应电流的导体在磁场中受安培力作用或通过电阻发热,又可使电能转化为机械能或电阻的内能,因此电磁感应过程总是伴随着能量的转化。
[例1]
在磁感应强度为B=1T的水平均强磁场中,竖直放置一个冂形金属框ABCD,框面垂直于磁场,宽度BC=1m
,质量1kg的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为1Ω,当杆自静止开始沿框架下滑时:
(1)从开始下滑到达到最大速度过程中重力势能转化为什么能量?
(2)若达到最大速度时下落了10m,安培力做了多少功?
解:(1)由能量守恒定律,重力做功减小的重力势能转化为使PQ加速增大的动能和热能
(2)50J
3、电磁感应中的能量问题
例2、θ=30?,L=1m,B=1T,导轨光滑电阻不计,F功率
恒定且为6W,m=0.2kg、R=1Ω,ab由由静止开始运动,
当s=2.8m时,获得稳定速度,在此过程中ab产生的热量
Q=5.8J,g=10m/s2,求:(1)ab棒的稳定速度
(2)ab棒从静止开始达到稳定速度所需时间。
基本方法:①用法拉第电磁感应定律和楞次定律确定感应动势的大小和方向。
②画出等效电路,求回路中电阻消耗电功率的表达式。
③分析导体机械能的变化,用能量守恒关系得到机械功率的改变与回路中电功率的改变所满足的方程。
3、电磁感应中的能量问题
1.如图所示,一宽40cm的匀强磁场区域,磁场方向垂直纸面向里.一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行.取它刚进入磁场的时刻t=0.
在下列图线中,正确反映感应电流随时间变化规律的是
思考:你能作出ad间电压与时间的关系图象吗?
[
c
]
4、电磁感应中的图象问题
2、如图所示竖直放置的螺线管和导线abcd构成回路,螺线管下方水平桌面上有一导体环。当导线abcd所围区域内的磁场按下列哪一图示方式变化时,导体环将受到向上的磁场力作用?
B
[
A
]
法拉第电磁感应定律
电磁感应规律综合应用的四种题型
2、电磁感应中的力学问题
1、电磁感应中的电路问题
3、电磁感应中的能量问题
4、电磁感应中的图象问题
1、电磁感应中的电路问题
如图所示,一个500匝的线圈的两端跟R=99Ω的电阻相连接,置于竖直向下的匀强磁场中,线圈的横截面积是20㎝2,电阻为1Ω,磁场的磁感应强度随时间变化的图象如图所示。求磁场变化过程中通过电阻R的电流为多大?
解析:由图b知,线圈中磁感应强度B均匀增加,其变
化率ΔB/Δt=(50-10)/4=10T/s.
1、电磁感应中的电路问题
基本方法:
1、用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向。
2、画等效电路。
3、运用闭合电路欧姆定律,串并联电路性质,电功率等公式联立求解。
等效电路图
1、电路方面:求感应电动势E,内外电路路端电压U,干支路电流I,消耗的电功率P
2、力学方面:匀速运动时所加外力F大小,外力功W,外力功功率P
如图,长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度ω匀速转动,磁场的磁感应强度为B,求杆OA两端的电势差.
例1
如图,有一匀强磁场B=1.0×10-3T,在垂直磁场的平面内,有一金属棒AO,绕平行于磁场的O轴顺时针转动,已知棒长L=0.20m,角速度ω=20rad/s,求:棒产生的感应电动势有多大?
练习1
如图所示,在磁感应强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架。OC为一端绕O点在框架上滑动的导体棒,OA之间连一个阻值为R的电阻(其余电阻都不计),若使OC以角速度ω匀速转动。试求:
(1)图中哪部分相当于电源?
(2)感应电动势E为多少?
(3)流过电阻R的电流I为多少?
练习2
(1)导体棒OC
(2)
(3)
3、把总电阻为2R的均匀电阻丝焊接成一半径为a的圆环,水平固定在竖直向下的磁感应强度为B的匀强磁场中,如图所示,一长度为2a,电阻为R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的接触,当金属棒以恒定速度v向右移动经过环心O时,求:
2、在圆环和金属棒上消耗的总功率
1、棒上的电流I大小,棒两端的电压U
4、如图所示,电阻不计的裸导体AB与宽为60cm的平行金属导轨良好接触,电阻R1=3Ω,
R2=6Ω,整个装置处在垂直导轨向里的匀强磁场中,磁感应强度B=0.5T。当AB向右以V=5m/s的速度匀速滑动时,求流过电阻R1、
R2的电流大小。
2、电磁感应中的力学问题
电磁感应中产生的感应电流在磁场中将受到安培力的作用,因此,电磁感应问题往往跟力学问题联系在一起,解决这类电磁感应中的力学问题,不仅要应用电磁学中的有关规律,如楞次定律、法拉第电磁感应定律、左右手定则、安培力的计算公式等,还要应用力学中的有关规律,如牛顿运动定律、动能定理、机械能守恒定律等。要将电磁学和力学的知识综合起来应用。
由于安培力和导体中的电流、运动速度均有关,
所以对磁场中运动导体进行动态分析十分必要。
【例1】水平放置于匀强磁场中的光滑导轨上,有一根导体棒ab,用恒力F作用在ab上,由静止开始运动,回路总电阻为R,分析ab
的运动情况,并求ab的最大速度。
a=(F-f)/m
v
E=BLv
I=
E/R
f=BIL
解:当f=F
时,a=0,速度达到最大,
F=f=BIL=B2
L2
vm
/R
vm=FR
/
B2
L2
vm称为收尾速度.
2、电磁感应中的力学问题
2、电磁感应中的力学问题
基本方法:
1、用法拉第电磁感应定律和楞次定律
求感应电动势的大小和方向。
2、求回路中的电流强度
3、分析导体受力情况(包含安培力,用左手定则)
4、列动力学方程求解。
【例2】
在磁感应强度为B的水平均强磁场中,竖直放置一个冂形金属框ABCD,框面垂直于磁场,宽度BC=L
,质量m的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为R,当杆自静止开始沿框架下滑时:
(1)开始下滑的加速度为多少?
(2)框内感应电流的方向怎样?安培力的方向?
(3)金属杆下滑的最大速度是多少?
解:(1)开始PQ受力为mg,
所以
a=g
(2)PQ向下加速运动,产生感应电流,方向顺时针,受到向上的磁场力F作用。
(3)达最大速度时,
F=BIL=B2
L2
vm
/R=mg
∴vm=mgR
/
B2
L2
【例3】已知:AB、CD足够长,L,θ,B,R。金属棒ab垂直于导轨放置,与导轨间的动摩擦因数为μ,质量为m,从静止开始沿导轨下滑,导轨和金属棒的电阻阻都不计。求ab棒下滑的最大速度
速度最大时做匀速运动
受力分析,列动力学方程
(1)金属杆刚进入磁场时的感应电动势;
(2)金属杆刚进入磁场时的加速度;
①感应电动势的大小
②感应电流的大小和方向
③使金属棒匀速运动所需的拉力
④感应电流的功率
⑤拉力的功率
【作业1】如图B=2T,金属棒ab向右匀速运动,v=5m/s,L=40cm,电阻R=2Ω,其余电阻不计,摩擦也不计,试求:
【作业2】宽1m,足够长的冂形金属框架竖直放置,一根质量是0.1kg,电阻0.1Ω的金属杆可沿框架无摩擦地滑动.金属杆MN下方0.8m处有一垂直框架平面的匀强磁场,磁感应强度是0.1T,金属杆MN由静止释放(如图).求:
【作业1】竖直放置冂形金属框架,宽1m,足够长,一根质量是0.1kg,电阻0.1Ω的金属杆可沿框架无摩擦地滑动.框架下部有一垂直框架平面的匀强磁场,磁感应强度是0.1T,金属杆MN自磁场边界上方0.8m处由静止释放(如图).求:
(1)金属杆刚进入磁场时的感应电动势;
(2)金属杆刚进入磁场时的加速度;
答:(1)
(2)
I=E/R=4A
F=BIL=0.4N
a=(mg-F)/m=6m/s2;
E=BLv=0.4V;
【作业2】如图B=2T,金属棒ab向右匀速运动,v=5m/s,
L=40cm,电阻R=2Ω,其余电阻不计,摩擦也不计,试
求:①感应电动势的大小
②感应电流的大小和方向
③使金属棒匀速运动所需的拉力
④感应电流的功率
⑤拉力的功率
右手定则
①
4v;
②
2A,b-a;
③
1.6N;
④
8w;
④
8w
3、电磁感应中的能量问题
4、电磁感应中的图象问题
能量转化特点:①导体切割磁感线或磁通量发生变化在回路中产生感应电流,机械能或其他形式的能量便转化为电能。
②具有感应电流的导体在磁场中受安培力作用或通过电阻发热,又可使电能转化为机械能或电阻的内能,因此电磁感应过程总是伴随着能量的转化。
[例1]
在磁感应强度为B=1T的水平均强磁场中,竖直放置一个冂形金属框ABCD,框面垂直于磁场,宽度BC=1m
,质量1kg的金属杆PQ用光滑金属套连接在框架AB和CD上如图.金属杆PQ电阻为1Ω,当杆自静止开始沿框架下滑时:
(1)从开始下滑到达到最大速度过程中重力势能转化为什么能量?
(2)若达到最大速度时下落了10m,安培力做了多少功?
解:(1)由能量守恒定律,重力做功减小的重力势能转化为使PQ加速增大的动能和热能
(2)50J
3、电磁感应中的能量问题
例2、θ=30?,L=1m,B=1T,导轨光滑电阻不计,F功率
恒定且为6W,m=0.2kg、R=1Ω,ab由由静止开始运动,
当s=2.8m时,获得稳定速度,在此过程中ab产生的热量
Q=5.8J,g=10m/s2,求:(1)ab棒的稳定速度
(2)ab棒从静止开始达到稳定速度所需时间。
基本方法:①用法拉第电磁感应定律和楞次定律确定感应动势的大小和方向。
②画出等效电路,求回路中电阻消耗电功率的表达式。
③分析导体机械能的变化,用能量守恒关系得到机械功率的改变与回路中电功率的改变所满足的方程。
3、电磁感应中的能量问题
1.如图所示,一宽40cm的匀强磁场区域,磁场方向垂直纸面向里.一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行.取它刚进入磁场的时刻t=0.
在下列图线中,正确反映感应电流随时间变化规律的是
思考:你能作出ad间电压与时间的关系图象吗?
[
c
]
4、电磁感应中的图象问题
2、如图所示竖直放置的螺线管和导线abcd构成回路,螺线管下方水平桌面上有一导体环。当导线abcd所围区域内的磁场按下列哪一图示方式变化时,导体环将受到向上的磁场力作用?
B
[
A
]
