人教版数学七年级上册4.2 课时1 直线、射线、线段 课件(21张)
文档属性
| 名称 | 人教版数学七年级上册4.2 课时1 直线、射线、线段 课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 23:05:48 | ||
图片预览





文档简介
第四章 几何图形初步
4.2 直线、射线、线段
课时1 直线、射线、线段
1.知道直线公理,知道点和直线的位置关系.(重点)
2.知道直线、射线、线段的表示方法.(重点,难点)
3.初步体会几何语言的应用.
学习目标
新课导入
我们在小学就已经学过线段、射线和直线,你能形象地说出它们的意义吗?你还能说说它们的联系与区别吗?这节课我们就开始进一步对它们的意义、表示法及联系进行研究.
新课讲解
知识点1 直线
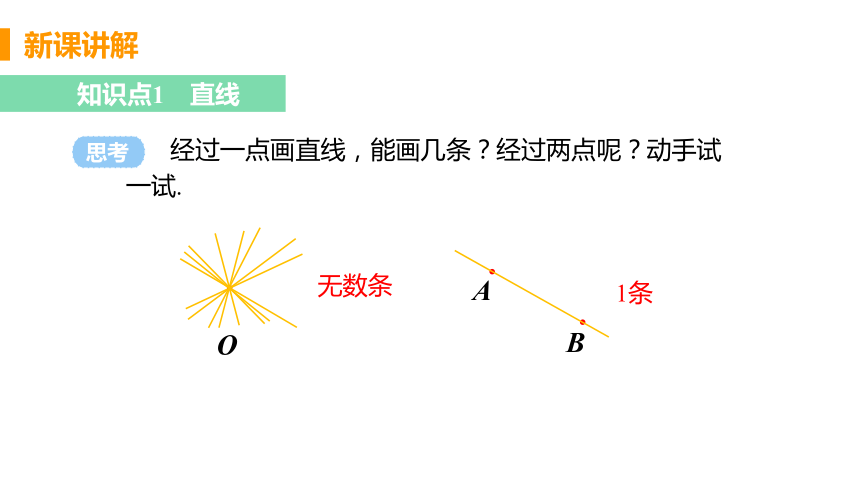
经过一点画直线,能画几条?经过两点呢?动手试一试.
思考
·
O
A
·
B
·
无数条
1条
新课讲解
结论
经过两点有一条直线,并且只有一条直线.即两点确定一条直线.
思考
你能找出生活中应用“两点确定一条直线”原理的例子吗?
新课讲解
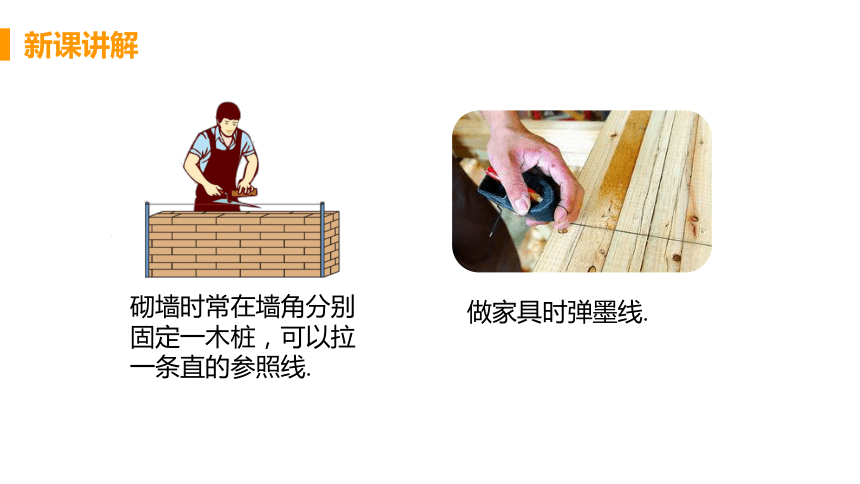
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
新课讲解
思考
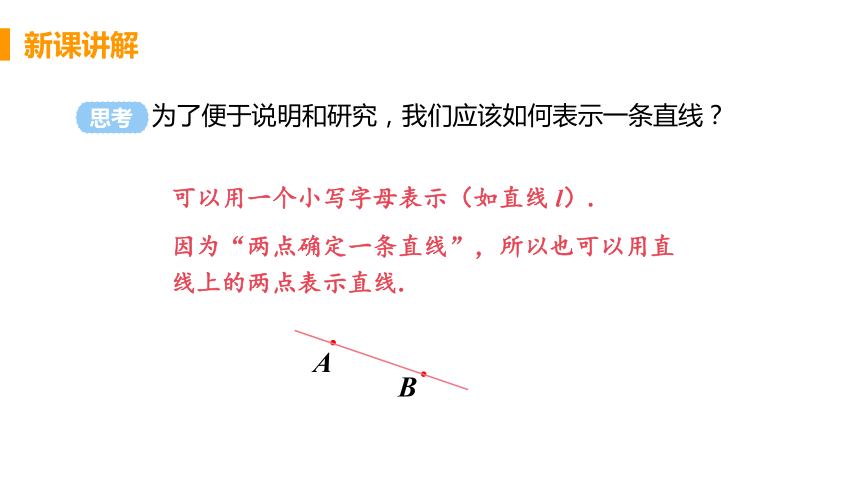
为了便于说明和研究,我们应该如何表示一条直线?
可以用一个小写字母表示(如直线 l).
因为“两点确定一条直线”,所以也可以用直线上的两点表示直线.
A
·
B
·
新课讲解
判断下列语句是否正确:
Ⅰ.一条直线可以表示为“直线 A”.
Ⅱ.一条直线可以表示为“直线 ab”.
Ⅲ.一条直线既可以记为“直线 AB”,又可以记为“直线 BA”,还可以记为“直线 m”.
×
×
新课讲解
思考
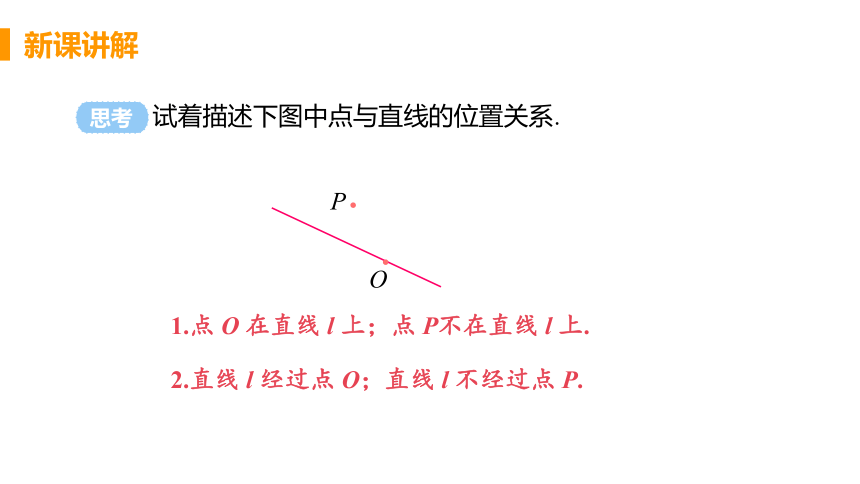
试着描述下图中点与直线的位置关系.
1.点 O 在直线 l 上;点 P不在直线 l 上.
2.直线 l 经过点 O;直线 l 不经过点 P.
·
P
·
O
新课讲解
根据前面的讨论,你能总结出点与直线的位置关系吗?
结论
点与直线的位置关系:
点在直线上(直线经过点);点不在直线上(直线不经过点).
新课讲解
思考
结论
我们应怎样描述直线与直线之间的关系呢?
直线 a 和直线 b 相交于点 O
a
·
O
b
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点.
新课讲解
练一练
用适当的语句描述图中点与直线的关系.
点 B 在直线 l 上;点 P、A不在直线 l 上.
点 A 在直线b、c交点上,点 B 在直线a、b交点上,点C在直线a、c交点上.
新课讲解
知识点2 射线和线段
思考
射线和线段都是直线的一部分,类比直线的表示方法,怎样恰当的表示射线和线段呢?
A B
O A
a
l
a
线段AB或线段a
射线OA或射线 l
思考
已知线段 AB,你能由线段 AB 得到直线 AB 和射线 AB 吗?
2.把线段向两个方向无限延伸可得到直线.
1.把线段向一个方向无限延伸可得到射线.
新课讲解
判断下列说法是否正确:
a.线段 AB 与射线 AB 都是直线 AB 的一部分.
b.直线 AB 与直线 BA 是同一条直线.
c.射线 AB 与射线 BA 是同一条射线.
d.端点重合的两条射线一定是同一条射线.
×
×
新课讲解
根据前面的讨论,你能总结出直线、射线、线段之间的关系吗?
结论
射线、线段都是直线的一部分;直线和射线不可度量.
新课讲解
新课讲解
练一练
1.按下列语句画出图形:
a.点A在线段MN上 b.射线AB不经过点P
c.经过点O的三条线段a、b、c
课堂小结
没有端点
直线
平面图形
射线
线段
1个端点
2个端点
当堂小练
1.下列语句准确规范的是( )
A.直线 a,b 相交于一点 m
B.延长直线 AB
C.延长射线 AD 到点 B ( A是端点)
D.直线 AB、CD 相交于点 M
D
当堂小练
2.在同一平面内有三个点A、B、C,过其中任意两个点画直线,可以画出的直线条数是多少?若过四个点 A、B、C、D 呢?
解:当A、B、C在同一直线上时,过其中任意两个点共可以作一条直线;当A、B、C不在同一直线上时,过其中任意两个点共可以作三条直线;当A、B、C、D在同一直线上时,过其中任意两个点共可以作一条直线;当A、B、C、D中有三个点在同一直线上时,过其中任意两个点共可以作四条直线;当A、B、C、D中均不在同一直线上时,过其中任意两个点共可以作六条直线.
D
拓展与延伸
温州
雁荡
台州
奉化
宁波
答:10种
往返温州、宁波两地的火车,中途需要停靠雁荡、台州、奉化三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
数学问题
实际问题
转 化 为
A B C D E
4.2 直线、射线、线段
课时1 直线、射线、线段
1.知道直线公理,知道点和直线的位置关系.(重点)
2.知道直线、射线、线段的表示方法.(重点,难点)
3.初步体会几何语言的应用.
学习目标
新课导入
我们在小学就已经学过线段、射线和直线,你能形象地说出它们的意义吗?你还能说说它们的联系与区别吗?这节课我们就开始进一步对它们的意义、表示法及联系进行研究.
新课讲解
知识点1 直线
经过一点画直线,能画几条?经过两点呢?动手试一试.
思考
·
O
A
·
B
·
无数条
1条
新课讲解
结论
经过两点有一条直线,并且只有一条直线.即两点确定一条直线.
思考
你能找出生活中应用“两点确定一条直线”原理的例子吗?
新课讲解
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
新课讲解
思考
为了便于说明和研究,我们应该如何表示一条直线?
可以用一个小写字母表示(如直线 l).
因为“两点确定一条直线”,所以也可以用直线上的两点表示直线.
A
·
B
·
新课讲解
判断下列语句是否正确:
Ⅰ.一条直线可以表示为“直线 A”.
Ⅱ.一条直线可以表示为“直线 ab”.
Ⅲ.一条直线既可以记为“直线 AB”,又可以记为“直线 BA”,还可以记为“直线 m”.
×
×
新课讲解
思考
试着描述下图中点与直线的位置关系.
1.点 O 在直线 l 上;点 P不在直线 l 上.
2.直线 l 经过点 O;直线 l 不经过点 P.
·
P
·
O
新课讲解
根据前面的讨论,你能总结出点与直线的位置关系吗?
结论
点与直线的位置关系:
点在直线上(直线经过点);点不在直线上(直线不经过点).
新课讲解
思考
结论
我们应怎样描述直线与直线之间的关系呢?
直线 a 和直线 b 相交于点 O
a
·
O
b
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点.
新课讲解
练一练
用适当的语句描述图中点与直线的关系.
点 B 在直线 l 上;点 P、A不在直线 l 上.
点 A 在直线b、c交点上,点 B 在直线a、b交点上,点C在直线a、c交点上.
新课讲解
知识点2 射线和线段
思考
射线和线段都是直线的一部分,类比直线的表示方法,怎样恰当的表示射线和线段呢?
A B
O A
a
l
a
线段AB或线段a
射线OA或射线 l
思考
已知线段 AB,你能由线段 AB 得到直线 AB 和射线 AB 吗?
2.把线段向两个方向无限延伸可得到直线.
1.把线段向一个方向无限延伸可得到射线.
新课讲解
判断下列说法是否正确:
a.线段 AB 与射线 AB 都是直线 AB 的一部分.
b.直线 AB 与直线 BA 是同一条直线.
c.射线 AB 与射线 BA 是同一条射线.
d.端点重合的两条射线一定是同一条射线.
×
×
新课讲解
根据前面的讨论,你能总结出直线、射线、线段之间的关系吗?
结论
射线、线段都是直线的一部分;直线和射线不可度量.
新课讲解
新课讲解
练一练
1.按下列语句画出图形:
a.点A在线段MN上 b.射线AB不经过点P
c.经过点O的三条线段a、b、c
课堂小结
没有端点
直线
平面图形
射线
线段
1个端点
2个端点
当堂小练
1.下列语句准确规范的是( )
A.直线 a,b 相交于一点 m
B.延长直线 AB
C.延长射线 AD 到点 B ( A是端点)
D.直线 AB、CD 相交于点 M
D
当堂小练
2.在同一平面内有三个点A、B、C,过其中任意两个点画直线,可以画出的直线条数是多少?若过四个点 A、B、C、D 呢?
解:当A、B、C在同一直线上时,过其中任意两个点共可以作一条直线;当A、B、C不在同一直线上时,过其中任意两个点共可以作三条直线;当A、B、C、D在同一直线上时,过其中任意两个点共可以作一条直线;当A、B、C、D中有三个点在同一直线上时,过其中任意两个点共可以作四条直线;当A、B、C、D中均不在同一直线上时,过其中任意两个点共可以作六条直线.
D
拓展与延伸
温州
雁荡
台州
奉化
宁波
答:10种
往返温州、宁波两地的火车,中途需要停靠雁荡、台州、奉化三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
数学问题
实际问题
转 化 为
A B C D E
