青岛六三版五上 5. 生活中的多边形-多边形的面积 同步习题(含答案)
文档属性
| 名称 | 青岛六三版五上 5. 生活中的多边形-多边形的面积 同步习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 16:47:22 | ||
图片预览


文档简介
5. 生活中的多边形-多边形的面积
一、单选题
1.一个平行四边形,底不变,高扩大到原来的5倍,它的面积(? ???)。
A.?扩大到原来的5倍????????????????B.?扩大到原来的25倍????????????????C.?不变????????????????D.?扩大到原来的15倍
2.(? ???)图形与其余2个的面积不一样大。
A.?????????????????????????B.?????????????????????????C.?
3.下图中,平行线间三个阴影图形的面积关系是( ???)。
A.?平行四边形的面积最大???????????B.?三角形的面积最大???????????C.?梯形的面积最大???????????D.?面积都相等
4.下面说法中错误的是(??? )。
A.? 三角形的面积公式是底乘高除以2
B.? 三角形的面积一定比它的周长大
C.? 周长相等的两个平行四边形,面积不一定相等
二、判断题
5.在一个平行四边形内画一个最大的三角形,三角形面积总是这个平行四边形面积的一半。
6.把一个平行四边形框架拉成一个长方形框架,面积会变大。
7.三角形的面积是平行四边形面积的一半.
8.周长相等的两个平行四边形的面积相等.
三、填空题
9.计算下面平行四边形的面积.
底是16.5m,高比底少4m.面积是________平方米.
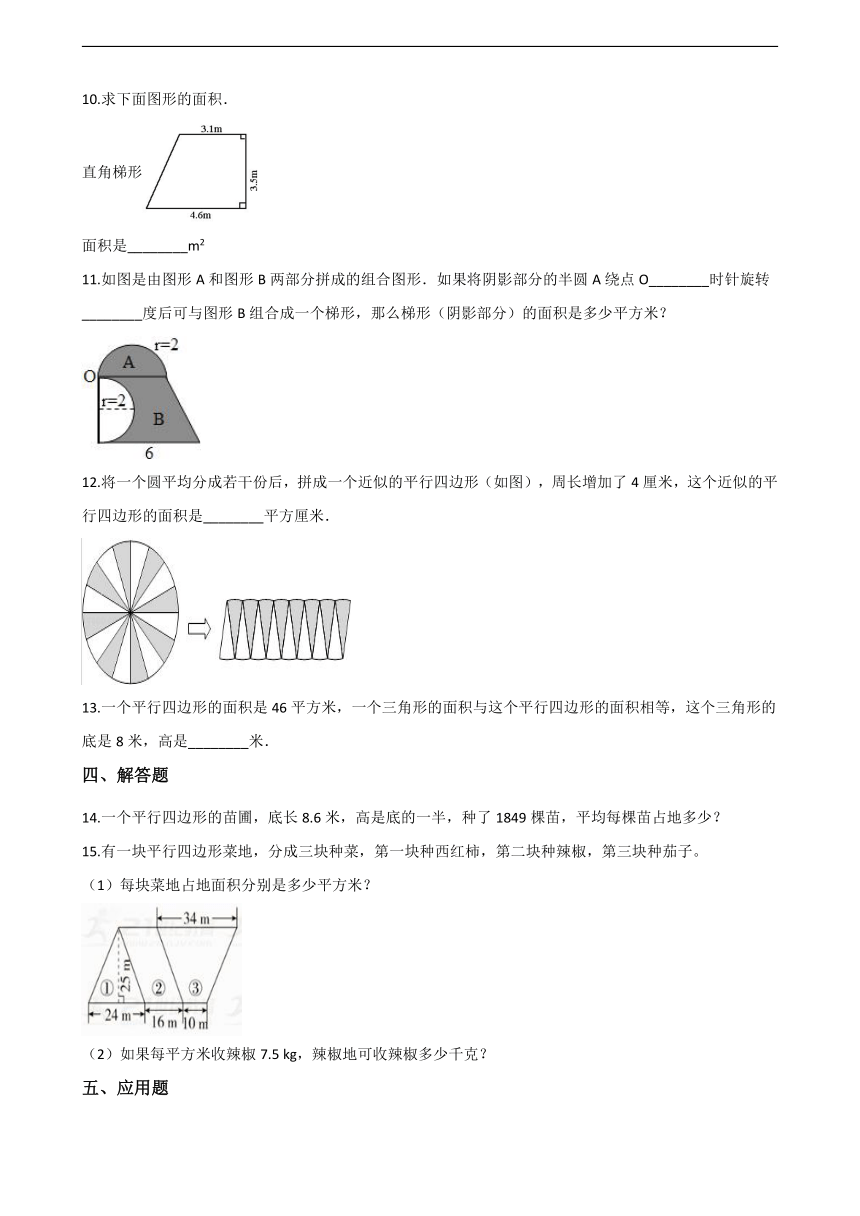
10.求下面图形的面积.
直角梯形
面积是________m2
11.如图是由图形A和图形B两部分拼成的组合图形.如果将阴影部分的半圆A绕点O________时针旋转________度后可与图形B组合成一个梯形,那么梯形(阴影部分)的面积是多少平方米?
12.将一个圆平均分成若干份后,拼成一个近似的平行四边形(如图),周长增加了4厘米,这个近似的平行四边形的面积是________平方厘米.
13.一个平行四边形的面积是46平方米,一个三角形的面积与这个平行四边形的面积相等,这个三角形的底是8米,高是________米.
四、解答题
14.一个平行四边形的苗圃,底长8.6米,高是底的一半,种了1849棵苗,平均每棵苗占地多少?
15.有一块平行四边形菜地,分成三块种菜,第一块种西红柿,第二块种辣椒,第三块种茄子。
(1)每块菜地占地面积分别是多少平方米?
(2)如果每平方米收辣椒7.5 kg,辣椒地可收辣椒多少千克?
五、应用题
16.图中阴影部分的面积一样大吗?为什么?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】一个平行四边形,底不变,高扩大到原来的5倍,它的面积扩大到原来的5倍.
故答案为:A.
【分析】因为平行四边形的面积=底×高, 如果底不变 , 它的高扩大a倍 , 则它的面积也扩大a倍,据此解答.
2.【答案】B
【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A图形的面积相等,B图形的面积与其余2个的面积不一样大.
故答案为:B.
【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.
3.【答案】D
【解析】【解答】解:平行四边形的面积=4×高,三角形的面积=8×高÷2=4×高,梯形的面积=(2+6)×高÷2=4×高,因为它们的高相等,所以它们的面积相等。
故答案为:D。
【分析】平行四边形的面积=底×高;三角形的面积=底×高÷2;梯形的面积=(上底+下底)×高÷2。
4.【答案】 B
【解析】【解答】面积和周长不是同样的单位,不能比较大小,所以三角形的面积一定比它的周长大错误。
故答案为:B。
【分析】三角形面积=底×高÷2,所以A正确;
平行四边形面积=底×高,所以周长相等的两个平行四边形,面积不一定相等,C正确。
二、判断题
5.【答案】正确
【解析】【解答】在一个平行四边形内画一个最大的三角形,三角形面积总是这个平行四边形面积的一半,此题说法正确.
故答案为:正确.【分析】要在平行四边形内画一个最大的三角形,那么所画的三角形必须与平行四边形等底等高,由此根据等底等高的三角形的面积是平行四边形面积的一半,即可做出判断.
6.【答案】正确
【解析】【解答】把一个平行四边形框架拉成一个长方形框架,面积会变大,原题说法正确.
故答案为:正确.
【分析】把一个平行四边形框架拉成一个长方形,它的底没变,但是高变长了,所以面积变大了,据此判断.
7.【答案】 错误
【解析】【解答】解:等底等高的三角形面积是平行四边形面积的一半,原题说法错误.
故答案为:错误
【分析】三角形面积=底×高÷2,平行四边形面积=底×高,所以只有等底等高的三角形面积才是平行四边形面积的一半.
8.【答案】错误
【解析】【解答】解答:周长相等的两个平行四边形的面积不一定相等.
周长相等的两个平行四边形,它们的高不一定相等,底也不一定相等.
【分析】判断两个平行四边形的面积是否相等,应分别判断它们的底和高的情况.
三、填空题
9.【答案】206.25
【解析】【解答】16.5×(16.5-4)
=16.5×12.5
=206.25(平方米)
故答案为:206.25
【分析】先计算出平行四边形的底,然后根据“平行四边形面积=底×高”列式计算面积.
10.【答案】13.475
【解析】【解答】
(3.1+4.6)×3.5÷2
=7.7×3.5÷2
=26.95÷2
=13.475(平方米)
【分析】这道题考查的是求梯形的面积的知识,解答此题梯形的面积=(上底+下底)×高÷2的公式,然后代入数据计算即可。
11.【答案】顺;90
【解析】【解答】解:如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形,
其面积为:(2×2+6)×(2×2)÷2,
=10×4÷2,
=40÷2,
=20(平方米);
答:梯形的面积是20平方米.
故答案为:顺、90.
【分析】由题意可知:如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形,梯形的上底和高都等于半圆的直径,下底已知,于是利用梯形的面积公式即可求解.此题主要考查梯形的面积的计算方法,关键是明白:梯形的上底和高都等于半圆的直径.
12.【答案】12.56
【解析】【解答】解:圆的半径:4÷2=2(厘米),
近似的平行四边形的面积=圆面积=3.14×22=3.14×4=12.56(平方厘米).
故答案为12.56.
【分析】将一个圆平均分成若干份后,拼成一个近似的平行四边形,周长增加了4厘米,这4厘米就是圆半径的2倍,因近似的平行四边形的面积等于圆的面积,即可可根据圆面积公式解答.本题考查了学生对图形拆分后的面积不变知识的掌握情况.
13.【答案】11.5
【解析】【解答】解:46×2÷8
=92÷8
=11.5(米)
答:高是11.5米.
故答案为:11.5.
【分析】根据平行四边形的面积与三角形的面积相等,可知一个三角形的面积是46平方米,再根据三角形的面积公式求出三角形的高,据此解答.
四、解答题
14.【答案】解:1849÷(8.6÷2×8.6)
=1849÷36.98
=50(平方米)
答:平均每棵树苗占地50平方米。
【解析】【分析】平行四边形面积=底×高,先计算出高再计算苗圃的面积,然后用树苗的棵数除以苗圃的面积即可求出平均每棵苗的占地面积。
15.【答案】 (1)解:24×25÷2=300(m2)
16×25=400(m2)
(10+34)×25÷2
=44×25÷2
=550(m2)
答:西红柿的面积是300平方米,辣椒的面积是400平方米,茄子的面积是550平方米。
(2)解:7.5×400=3000(kg)
答:辣椒地可收辣椒3000千克。
【解析】【分析】三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,根据公式分别计算面积。用辣椒地的面积乘每平方米收辣椒的重量即可求出收辣椒的总重量。
五、应用题
16.【答案】解:面积一样大
假设正方体的边长为4.则:
A、B、C、D、E中阴影部分的面积为
F中阴影部分的面积为:
答:图中阴影部分的面积一样大.
【解析】【分析】前5个图形中阴影部分的面积都是大正方形面积减去一个直径是正方形边长的圆的面积;最后一个图形阴影部分的面积是正方形面积减去四个小圆的面积;由此假设出正方形的边长,计算后判断阴影部分的面积大小即可.
一、单选题
1.一个平行四边形,底不变,高扩大到原来的5倍,它的面积(? ???)。
A.?扩大到原来的5倍????????????????B.?扩大到原来的25倍????????????????C.?不变????????????????D.?扩大到原来的15倍
2.(? ???)图形与其余2个的面积不一样大。
A.?????????????????????????B.?????????????????????????C.?
3.下图中,平行线间三个阴影图形的面积关系是( ???)。
A.?平行四边形的面积最大???????????B.?三角形的面积最大???????????C.?梯形的面积最大???????????D.?面积都相等
4.下面说法中错误的是(??? )。
A.? 三角形的面积公式是底乘高除以2
B.? 三角形的面积一定比它的周长大
C.? 周长相等的两个平行四边形,面积不一定相等
二、判断题
5.在一个平行四边形内画一个最大的三角形,三角形面积总是这个平行四边形面积的一半。
6.把一个平行四边形框架拉成一个长方形框架,面积会变大。
7.三角形的面积是平行四边形面积的一半.
8.周长相等的两个平行四边形的面积相等.
三、填空题
9.计算下面平行四边形的面积.
底是16.5m,高比底少4m.面积是________平方米.
10.求下面图形的面积.
直角梯形
面积是________m2
11.如图是由图形A和图形B两部分拼成的组合图形.如果将阴影部分的半圆A绕点O________时针旋转________度后可与图形B组合成一个梯形,那么梯形(阴影部分)的面积是多少平方米?
12.将一个圆平均分成若干份后,拼成一个近似的平行四边形(如图),周长增加了4厘米,这个近似的平行四边形的面积是________平方厘米.
13.一个平行四边形的面积是46平方米,一个三角形的面积与这个平行四边形的面积相等,这个三角形的底是8米,高是________米.
四、解答题
14.一个平行四边形的苗圃,底长8.6米,高是底的一半,种了1849棵苗,平均每棵苗占地多少?
15.有一块平行四边形菜地,分成三块种菜,第一块种西红柿,第二块种辣椒,第三块种茄子。
(1)每块菜地占地面积分别是多少平方米?
(2)如果每平方米收辣椒7.5 kg,辣椒地可收辣椒多少千克?
五、应用题
16.图中阴影部分的面积一样大吗?为什么?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】一个平行四边形,底不变,高扩大到原来的5倍,它的面积扩大到原来的5倍.
故答案为:A.
【分析】因为平行四边形的面积=底×高, 如果底不变 , 它的高扩大a倍 , 则它的面积也扩大a倍,据此解答.
2.【答案】B
【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A图形的面积相等,B图形的面积与其余2个的面积不一样大.
故答案为:B.
【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.
3.【答案】D
【解析】【解答】解:平行四边形的面积=4×高,三角形的面积=8×高÷2=4×高,梯形的面积=(2+6)×高÷2=4×高,因为它们的高相等,所以它们的面积相等。
故答案为:D。
【分析】平行四边形的面积=底×高;三角形的面积=底×高÷2;梯形的面积=(上底+下底)×高÷2。
4.【答案】 B
【解析】【解答】面积和周长不是同样的单位,不能比较大小,所以三角形的面积一定比它的周长大错误。
故答案为:B。
【分析】三角形面积=底×高÷2,所以A正确;
平行四边形面积=底×高,所以周长相等的两个平行四边形,面积不一定相等,C正确。
二、判断题
5.【答案】正确
【解析】【解答】在一个平行四边形内画一个最大的三角形,三角形面积总是这个平行四边形面积的一半,此题说法正确.
故答案为:正确.【分析】要在平行四边形内画一个最大的三角形,那么所画的三角形必须与平行四边形等底等高,由此根据等底等高的三角形的面积是平行四边形面积的一半,即可做出判断.
6.【答案】正确
【解析】【解答】把一个平行四边形框架拉成一个长方形框架,面积会变大,原题说法正确.
故答案为:正确.
【分析】把一个平行四边形框架拉成一个长方形,它的底没变,但是高变长了,所以面积变大了,据此判断.
7.【答案】 错误
【解析】【解答】解:等底等高的三角形面积是平行四边形面积的一半,原题说法错误.
故答案为:错误
【分析】三角形面积=底×高÷2,平行四边形面积=底×高,所以只有等底等高的三角形面积才是平行四边形面积的一半.
8.【答案】错误
【解析】【解答】解答:周长相等的两个平行四边形的面积不一定相等.
周长相等的两个平行四边形,它们的高不一定相等,底也不一定相等.
【分析】判断两个平行四边形的面积是否相等,应分别判断它们的底和高的情况.
三、填空题
9.【答案】206.25
【解析】【解答】16.5×(16.5-4)
=16.5×12.5
=206.25(平方米)
故答案为:206.25
【分析】先计算出平行四边形的底,然后根据“平行四边形面积=底×高”列式计算面积.
10.【答案】13.475
【解析】【解答】
(3.1+4.6)×3.5÷2
=7.7×3.5÷2
=26.95÷2
=13.475(平方米)
【分析】这道题考查的是求梯形的面积的知识,解答此题梯形的面积=(上底+下底)×高÷2的公式,然后代入数据计算即可。
11.【答案】顺;90
【解析】【解答】解:如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形,
其面积为:(2×2+6)×(2×2)÷2,
=10×4÷2,
=40÷2,
=20(平方米);
答:梯形的面积是20平方米.
故答案为:顺、90.
【分析】由题意可知:如果将阴影部分的半圆A绕点O顺时针旋转90度后可与图形B组合成一个梯形,梯形的上底和高都等于半圆的直径,下底已知,于是利用梯形的面积公式即可求解.此题主要考查梯形的面积的计算方法,关键是明白:梯形的上底和高都等于半圆的直径.
12.【答案】12.56
【解析】【解答】解:圆的半径:4÷2=2(厘米),
近似的平行四边形的面积=圆面积=3.14×22=3.14×4=12.56(平方厘米).
故答案为12.56.
【分析】将一个圆平均分成若干份后,拼成一个近似的平行四边形,周长增加了4厘米,这4厘米就是圆半径的2倍,因近似的平行四边形的面积等于圆的面积,即可可根据圆面积公式解答.本题考查了学生对图形拆分后的面积不变知识的掌握情况.
13.【答案】11.5
【解析】【解答】解:46×2÷8
=92÷8
=11.5(米)
答:高是11.5米.
故答案为:11.5.
【分析】根据平行四边形的面积与三角形的面积相等,可知一个三角形的面积是46平方米,再根据三角形的面积公式求出三角形的高,据此解答.
四、解答题
14.【答案】解:1849÷(8.6÷2×8.6)
=1849÷36.98
=50(平方米)
答:平均每棵树苗占地50平方米。
【解析】【分析】平行四边形面积=底×高,先计算出高再计算苗圃的面积,然后用树苗的棵数除以苗圃的面积即可求出平均每棵苗的占地面积。
15.【答案】 (1)解:24×25÷2=300(m2)
16×25=400(m2)
(10+34)×25÷2
=44×25÷2
=550(m2)
答:西红柿的面积是300平方米,辣椒的面积是400平方米,茄子的面积是550平方米。
(2)解:7.5×400=3000(kg)
答:辣椒地可收辣椒3000千克。
【解析】【分析】三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,根据公式分别计算面积。用辣椒地的面积乘每平方米收辣椒的重量即可求出收辣椒的总重量。
五、应用题
16.【答案】解:面积一样大
假设正方体的边长为4.则:
A、B、C、D、E中阴影部分的面积为
F中阴影部分的面积为:
答:图中阴影部分的面积一样大.
【解析】【分析】前5个图形中阴影部分的面积都是大正方形面积减去一个直径是正方形边长的圆的面积;最后一个图形阴影部分的面积是正方形面积减去四个小圆的面积;由此假设出正方形的边长,计算后判断阴影部分的面积大小即可.
