人教版八年级上册数学课件:12.1全等三角形(共18张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:12.1全等三角形(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
12.1全等三角形
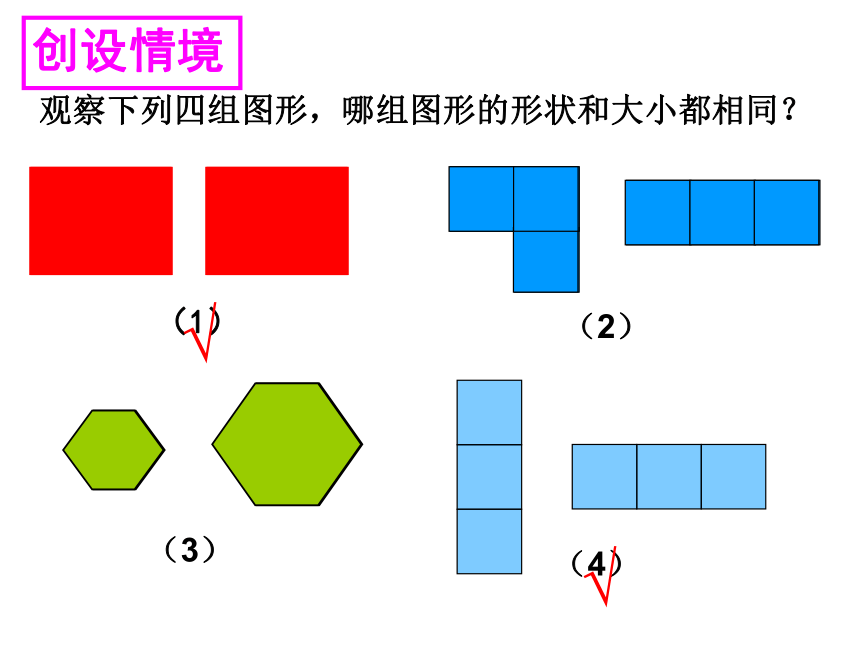
创设情境
观察下列四组图形,哪组图形的形状和大小都相同?
(1)
(2)
(3)
(4)
√
√
创设情境
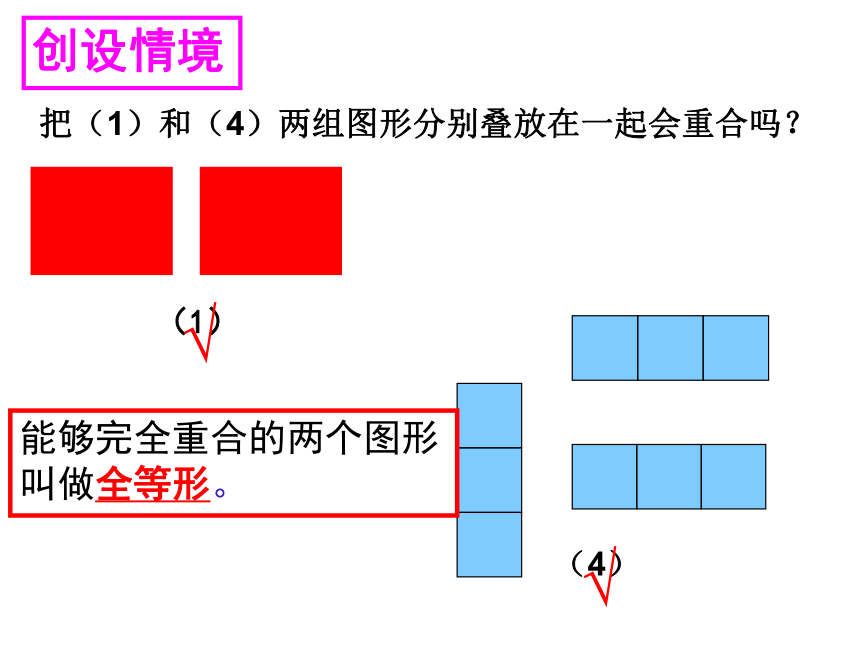
把(1)和(4)两组图形分别叠放在一起会重合吗?
(1)
(4)
√
√
能够完全重合的两个图形叫做全等形。
探究新知
A
B
C
D
E
F
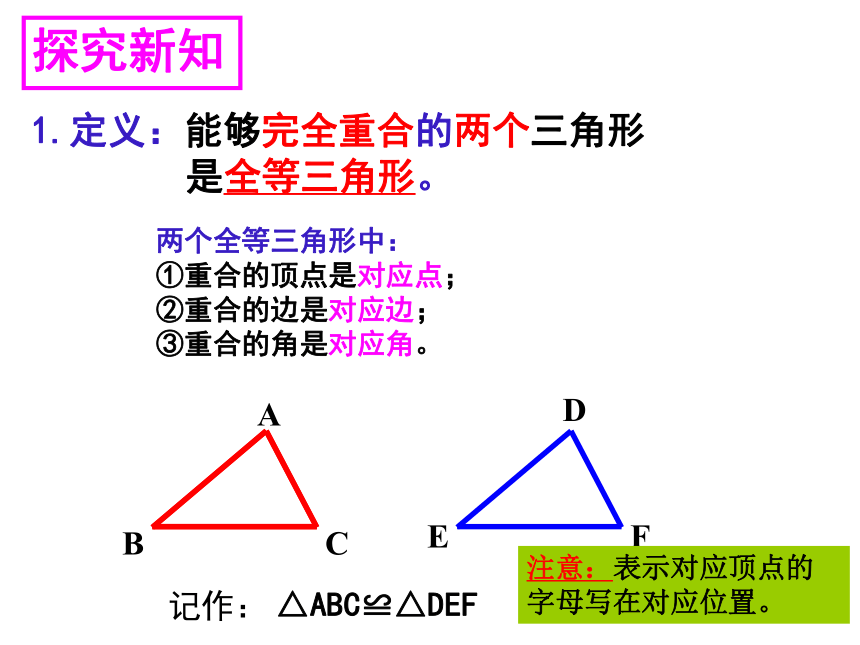
1.定义:能够完全重合的两个三角形
是全等三角形。
两个全等三角形中:
①重合的顶点是对应点;
②重合的边是对应边;
③重合的角是对应角。
记作:
△ABC≌△DEF
注意:表示对应顶点的字母写在对应位置。
A
B
C
D
E
F
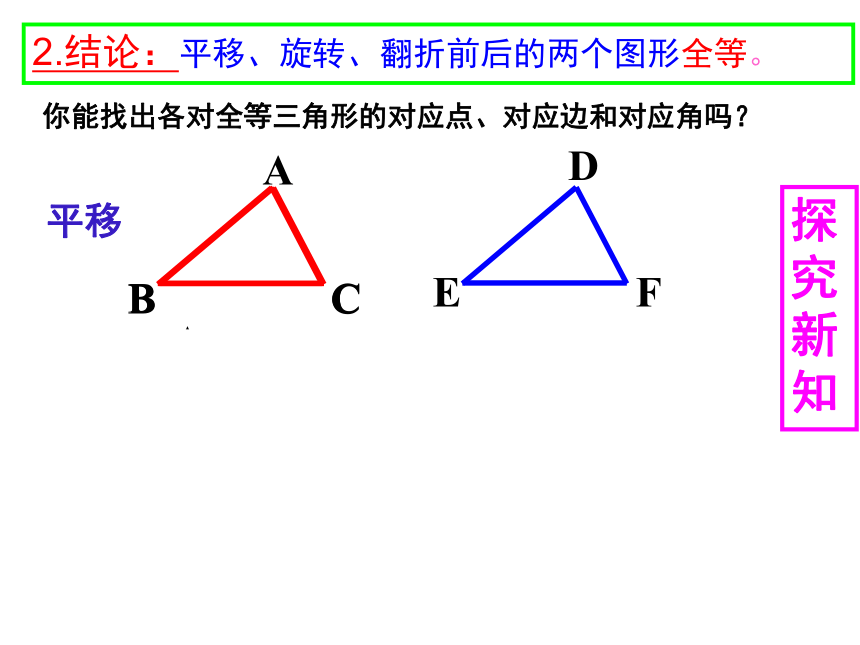
2.结论:平移、旋转、翻折前后的两个图形全等。
B
C
平移
旋转
翻折
你能找出各对全等三角形的对应点、对应边和对应角吗?
探
究
新
知
探究新知
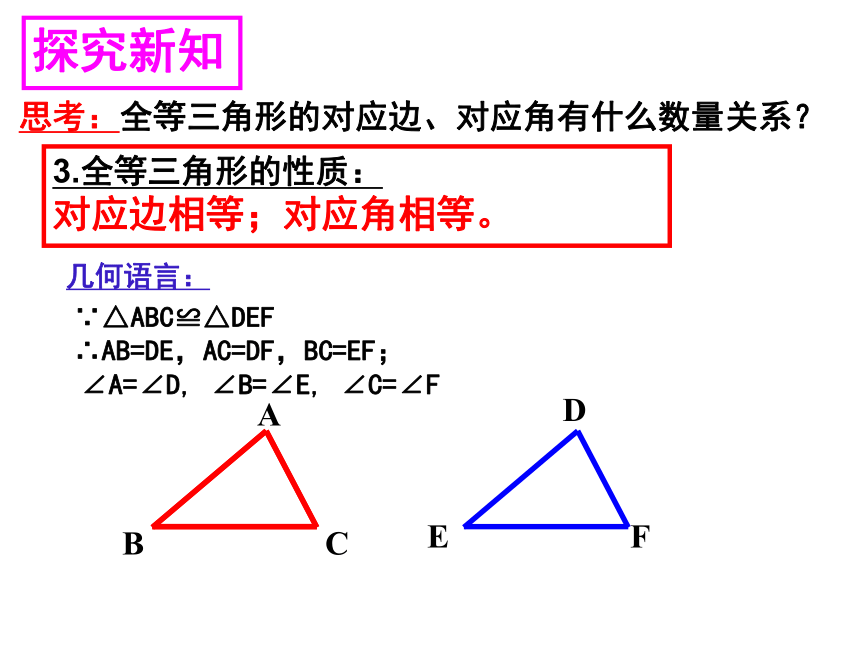
思考:全等三角形的对应边、对应角有什么数量关系?
A
B
C
D
E
F
3.全等三角形的性质:
对应边相等;对应角相等。
几何语言:
∠A=∠D,
∠B=∠E,
∠C=∠F
∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF;
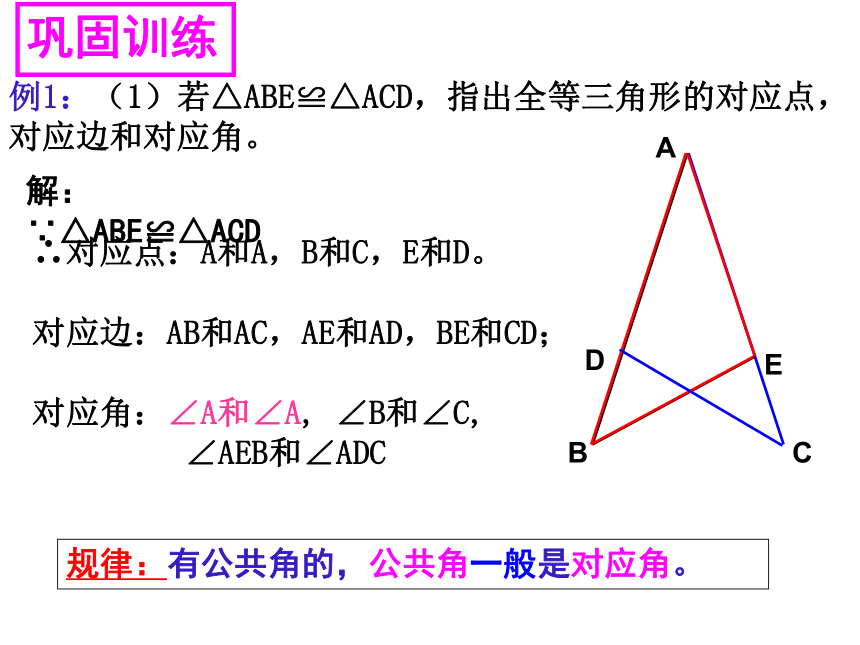
例1:(1)若△ABE≌△ACD,指出全等三角形的对应点,对应边和对应角。
A
B
D
E
C
解:∵△ABE≌△ACD
规律:有公共角的,公共角一般是对应角。
巩固训练
∴对应点:A和A,B和C,E和D。
对应边:AB和AC,AE和AD,BE和CD;
对应角:∠A和∠A,
∠B和∠C,
∠AEB和∠ADC
(2)若△ABC≌△CDA,找出相等的边和相等的角。
解:∵△ABC≌△CDA
∴AB=CD,AC=AC,BC=AD;
∠BAC=∠ACD,
∠B=∠D,
∠ACB=∠CAD
规律:有公共边的,公共边一般是对应边。
巩固训练
A
C
B
O
D
(3)若△AOC≌△BOD,找出图中相等的边和相等的角。
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD;
∠A=∠B,
∠AOC=∠BOD,
∠C=∠D。
规律:有对顶角的,对顶角一般是对应角。
巩固训练
巩固训练
例2:如图△ABC≌△DEC,CA和CD,CB和CE是对应边,∠BCE和∠ACD相等吗?为什么?
∵△ABC≌△DEC
∴∠ACB=∠DCE
∴∠ACB-∠ACE=∠DCE-∠ACE,
即∠BCE=∠ACD。
解:∠BCE=∠ACD,理由如下:
巩固训练
练习1:如图,△ABN≌△CBM,∠A和∠C是对应角,AB和BC是对应边,求证:AM=NC。
证明:∵△ABN≌△CBM
∴AN=MC
∴AN-MN=MC-MN,
即AM=NC。
练习2.如图△ABE≌△ACD,AB与AC,AD与AE是对应边,∠A=40°,∠B=30°,求∠ADC的大小。
解:∵△ABE≌△ACD(已知)
∴∠C=∠B=30°
∴∠ADC=180°-∠C-∠A=110°
巩固训练
拓展延伸
1.判断题。
(1)全等三角形的对应边相等,对应角相等。(
)
(2)全等三角形的周长相等。
(
)
(3)面积相等的三角形是全等三角形。
(
)
(4)全等的三角形面积相等。
(
)
√
√
√
×
2.选择题:
(1)如图将△ABC平移,得到△DEF,如果AB=6cm,AC=5cm,BC=7cm,那么EF的长是(
)
A.7cm
B.6cm
C.5cm
D.无法确定
(2)在上题中,
如果CF=3cm,那么BE的长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
A
B
拓展延伸
拓展延伸
3.如图,
△ABD
≌
△EBC,
如果AB=3cm,BC=5cm,
求BE、BD的长.
即BE=3cm,BD=5cm
解:∵△ABD
≌
△EBC
∴AB=EB=3cm,BC=BD=5cm
拓展延伸
4.如图,
△ABD
≌
△EBC,如果AB=3cm,DE=2cm,求BC的长.
解:∵△ABD
≌
△EBC
∴AB=BE,BC=BD
∴BC=BD=DE+BE
=DE+AB=2+3=5cm
归纳提升
全等形:能够完全重合的两个图形。
全等三角形:
1.定义:能够完全重合的两个三角形
是全等三角形。(△ABC≌△DEF)
2.结论:平移、旋转、翻折前后的两个图形全等。
3.性质:全等三角形的对应边相等、对应角相等。
1、猜一猜:(如图)下面两个三角形是否全等?
2、想一想:如何判断两个三角形全等呢?
思维拓展
12.1全等三角形
创设情境
观察下列四组图形,哪组图形的形状和大小都相同?
(1)
(2)
(3)
(4)
√
√
创设情境
把(1)和(4)两组图形分别叠放在一起会重合吗?
(1)
(4)
√
√
能够完全重合的两个图形叫做全等形。
探究新知
A
B
C
D
E
F
1.定义:能够完全重合的两个三角形
是全等三角形。
两个全等三角形中:
①重合的顶点是对应点;
②重合的边是对应边;
③重合的角是对应角。
记作:
△ABC≌△DEF
注意:表示对应顶点的字母写在对应位置。
A
B
C
D
E
F
2.结论:平移、旋转、翻折前后的两个图形全等。
B
C
平移
旋转
翻折
你能找出各对全等三角形的对应点、对应边和对应角吗?
探
究
新
知
探究新知
思考:全等三角形的对应边、对应角有什么数量关系?
A
B
C
D
E
F
3.全等三角形的性质:
对应边相等;对应角相等。
几何语言:
∠A=∠D,
∠B=∠E,
∠C=∠F
∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF;
例1:(1)若△ABE≌△ACD,指出全等三角形的对应点,对应边和对应角。
A
B
D
E
C
解:∵△ABE≌△ACD
规律:有公共角的,公共角一般是对应角。
巩固训练
∴对应点:A和A,B和C,E和D。
对应边:AB和AC,AE和AD,BE和CD;
对应角:∠A和∠A,
∠B和∠C,
∠AEB和∠ADC
(2)若△ABC≌△CDA,找出相等的边和相等的角。
解:∵△ABC≌△CDA
∴AB=CD,AC=AC,BC=AD;
∠BAC=∠ACD,
∠B=∠D,
∠ACB=∠CAD
规律:有公共边的,公共边一般是对应边。
巩固训练
A
C
B
O
D
(3)若△AOC≌△BOD,找出图中相等的边和相等的角。
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD;
∠A=∠B,
∠AOC=∠BOD,
∠C=∠D。
规律:有对顶角的,对顶角一般是对应角。
巩固训练
巩固训练
例2:如图△ABC≌△DEC,CA和CD,CB和CE是对应边,∠BCE和∠ACD相等吗?为什么?
∵△ABC≌△DEC
∴∠ACB=∠DCE
∴∠ACB-∠ACE=∠DCE-∠ACE,
即∠BCE=∠ACD。
解:∠BCE=∠ACD,理由如下:
巩固训练
练习1:如图,△ABN≌△CBM,∠A和∠C是对应角,AB和BC是对应边,求证:AM=NC。
证明:∵△ABN≌△CBM
∴AN=MC
∴AN-MN=MC-MN,
即AM=NC。
练习2.如图△ABE≌△ACD,AB与AC,AD与AE是对应边,∠A=40°,∠B=30°,求∠ADC的大小。
解:∵△ABE≌△ACD(已知)
∴∠C=∠B=30°
∴∠ADC=180°-∠C-∠A=110°
巩固训练
拓展延伸
1.判断题。
(1)全等三角形的对应边相等,对应角相等。(
)
(2)全等三角形的周长相等。
(
)
(3)面积相等的三角形是全等三角形。
(
)
(4)全等的三角形面积相等。
(
)
√
√
√
×
2.选择题:
(1)如图将△ABC平移,得到△DEF,如果AB=6cm,AC=5cm,BC=7cm,那么EF的长是(
)
A.7cm
B.6cm
C.5cm
D.无法确定
(2)在上题中,
如果CF=3cm,那么BE的长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
A
B
拓展延伸
拓展延伸
3.如图,
△ABD
≌
△EBC,
如果AB=3cm,BC=5cm,
求BE、BD的长.
即BE=3cm,BD=5cm
解:∵△ABD
≌
△EBC
∴AB=EB=3cm,BC=BD=5cm
拓展延伸
4.如图,
△ABD
≌
△EBC,如果AB=3cm,DE=2cm,求BC的长.
解:∵△ABD
≌
△EBC
∴AB=BE,BC=BD
∴BC=BD=DE+BE
=DE+AB=2+3=5cm
归纳提升
全等形:能够完全重合的两个图形。
全等三角形:
1.定义:能够完全重合的两个三角形
是全等三角形。(△ABC≌△DEF)
2.结论:平移、旋转、翻折前后的两个图形全等。
3.性质:全等三角形的对应边相等、对应角相等。
1、猜一猜:(如图)下面两个三角形是否全等?
2、想一想:如何判断两个三角形全等呢?
思维拓展
