人教版数学 (七升八) 暑假预习课:第十四章整式的乘法与因式分解学案(无答案)
文档属性
| 名称 | 人教版数学 (七升八) 暑假预习课:第十四章整式的乘法与因式分解学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 374.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 00:00:00 | ||
图片预览




文档简介
八上数学《整式的乘法与因式分解》暑假预习课
(基础)知识讲解
学案
【学习目标】
1.
掌握整数幂的运算性质,并能运用它们熟练地进行运算;掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算;
2.
掌握乘法公式(平方差公式和完全平方公式),能利用公式进行乘法运算;
3.
掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算;
4.掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解.
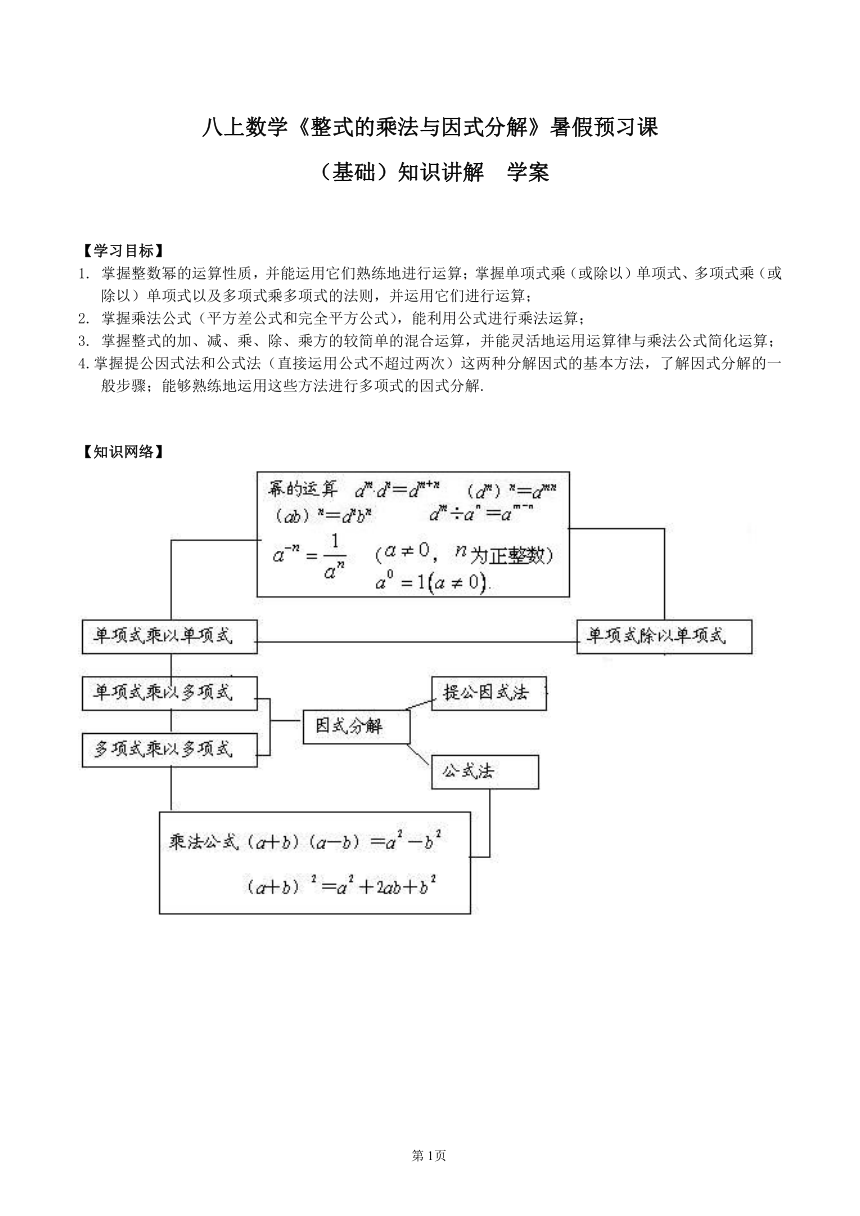
【知识网络】
【要点梳理】
要点一、幂的运算
1.同底数幂的乘法:(为正整数);同底数幂相乘,底数不变,指数相加.
2.幂的乘方:
(为正整数);幂的乘方,底数不变,指数相乘.
3.积的乘方:
(为正整数);积的乘方,等于各因数乘方的积.
4.同底数幂的除法:(≠0,
为正整数,并且).
同底数幂相除,底数不变,指数相减.
5.零指数幂:即任何不等于零的数的零次方等于1.
6.负指数幂:(,为正整数).任何不等于0的数的-次幂,等于这个数的次幂的倒数.
【同步练习】
一.选择题
1.计算的x3乘以x2结果是( )
A.x6
B.6x
C.
x5
D.
5x
2.的值是(
).
A.
B.
C.
D.
3.下列计算正确的是(
).
A.
B.
C.
D.
4.下列各题中,计算结果写成10的幂的形式,其中正确的是(
).
A.
100×=
B.
1000×=
C.
100×=
D.
100×1000=
5.下列计算正确的是(
).
A.
B.
C.
D.
6.若成立,则(
).
A.
=6,=12
B.
=3,=12
C.
=3,=5
D.
=6,=5
二.填空题
7.
已知5x=6,5y=3,则5x+2y=
.
8.
若,则=_______.
9.
已知,那么______.
10.若,则=______;若,则=______.
11.
______;
______;
=______.
12.若n
是正整数,且,则=__________.
三.解答题
13.(1)若,求的值.
(2)若,求、的值.
要点二、整式的乘法
1.单项式乘以单项式
单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
2.单项式乘以多项式
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.即(都是单项式).
3.多项式乘以多项式
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即.
要点诠释:运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:.
【巩固练习】
一.选择题
1.下列算式中正确的是(
).
A.
B.
C.
D.
2.的结果是(
).
A
.
B.
C.
D.
3.下列各式计算正确的是( )
A.x(x2﹣x﹣1)=x3﹣x﹣1
B.ab(a+b)=a2+b2
C.3x(x2﹣2x﹣1)=3x3﹣6x2﹣3x
D.﹣2x(x2﹣x﹣1)=﹣2x3﹣2x2+2x
4.已知,那么的值为(
).
A.-2
B.2
C.-5
D.5
5.
要使成立,则,的值分别是(
).
A.
B.
C.
D.
6.设M=,N=,则M与N的关系为(
).
A.M<N
B.M>N
C.M=N
D.不能确定
二.填空题
7.
已知三角形的底边为,高是,则三角形的面积是_________.
8.
计算:①=________;②=______;
③=_______;④=______.
9.
方程的解为________.
10.
.
11.
若化简(ax+3y)(x﹣y)的结果中不含xy项,则a的值为
.
12.
若,,则=____________.
三.解答题
14.
解下列各方程.
(1)
(2)
15.
化简求值:
(1),其中.
(2),其中.
要点三、乘法公式
1.平方差公式:
两个数的和与这两个数的差的积,等于这两个数的平方差.
要点诠释:在这里,既可以是具体数字,也可以是单项式或多项式.
平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.
2.
完全平方公式:;
两数和
(差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.
要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍.
【巩固练习】
一.选择题
1.
在下列计算中,不能用平方差公式计算的是(
)
A.
B.
C.
D.
2.若=6,=5,则等于(
).
A.11
B.15
C.30
D.60
3.下列计算正确的是(
).
A.=
B.
=
C.
D.(
)()=
4.下列多项式不是完全平方式的是(
).
A.
B.
C.
D.
5.已知关于x的二次三项式4x2﹣mx+25是完全平方式,则常数m的值为( )
A.10
B.±10
C.﹣20
D.±20
6.下列等式不能恒成立的是(
).
A.
B.
C.
D.
二.填空题
7.若是一个完全平方式,则=______.
8.
若=,则M
=______.
9.
若=3,=1,则=_______.
10.(2015春?陕西校级期末)(1+x)(1﹣x)(1+x2)(1+x4)=
.
11.
___________.
12.若,则代数式的值为________.
三.解答题
13.先化简,再求值:,其中.
14.已知:,且求的值.
要点四、因式分解
把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
因式分解的方法主要有:
提公因式法,
公式法,
分组分解法,
十字相乘法,
添、拆项法等.
要点诠释:落实好方法的综合运用:
首先提取公因式,然后考虑用公式;
两项平方或立方,三项完全或十字;
四项以上想分组,分组分得要合适;
几种方法反复试,最后须是连乘式;
因式分解要彻底,一次一次又一次.
【巩固练习】
一.选择题
1.
下列各式变形中,是因式分解的是(
)
A.
B.
C.
D.
2.
多项式6abc﹣3a2bc+12ab的公因式是( )
A.abc
B.3ab
C.3abc
D.3ab
3.
多项式分解因式的结果是(
)
A.
B.
C.
D.
4.
分解因式的结果是(
)
A.
B.
C.
D.
5.
下列因式分解正确的是(
)
A.
B.
C.
D.
6.
把提公因式得(
)
A.
B.
C.
D.
二.填空题
7.
因式分解是把一个______________化为______________的形式.
8.
的公因式是___________;的公因式是__________.
9.
因式分解=_________________.
10.
多项式的公因式是______________.
11.分解因式:m(x﹣y)+n(y﹣x)=_____________________.
12.
因式分解=_____________________.
三.解答题
13.
应用简便方法计算:
(1);
(2)
14.已知,求和的值.
15.分解因式:6a(b﹣1)﹣2(1﹣b).
PAGE
第1页
(基础)知识讲解
学案
【学习目标】
1.
掌握整数幂的运算性质,并能运用它们熟练地进行运算;掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算;
2.
掌握乘法公式(平方差公式和完全平方公式),能利用公式进行乘法运算;
3.
掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算;
4.掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解.
【知识网络】
【要点梳理】
要点一、幂的运算
1.同底数幂的乘法:(为正整数);同底数幂相乘,底数不变,指数相加.
2.幂的乘方:
(为正整数);幂的乘方,底数不变,指数相乘.
3.积的乘方:
(为正整数);积的乘方,等于各因数乘方的积.
4.同底数幂的除法:(≠0,
为正整数,并且).
同底数幂相除,底数不变,指数相减.
5.零指数幂:即任何不等于零的数的零次方等于1.
6.负指数幂:(,为正整数).任何不等于0的数的-次幂,等于这个数的次幂的倒数.
【同步练习】
一.选择题
1.计算的x3乘以x2结果是( )
A.x6
B.6x
C.
x5
D.
5x
2.的值是(
).
A.
B.
C.
D.
3.下列计算正确的是(
).
A.
B.
C.
D.
4.下列各题中,计算结果写成10的幂的形式,其中正确的是(
).
A.
100×=
B.
1000×=
C.
100×=
D.
100×1000=
5.下列计算正确的是(
).
A.
B.
C.
D.
6.若成立,则(
).
A.
=6,=12
B.
=3,=12
C.
=3,=5
D.
=6,=5
二.填空题
7.
已知5x=6,5y=3,则5x+2y=
.
8.
若,则=_______.
9.
已知,那么______.
10.若,则=______;若,则=______.
11.
______;
______;
=______.
12.若n
是正整数,且,则=__________.
三.解答题
13.(1)若,求的值.
(2)若,求、的值.
要点二、整式的乘法
1.单项式乘以单项式
单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
2.单项式乘以多项式
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.即(都是单项式).
3.多项式乘以多项式
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即.
要点诠释:运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:.
【巩固练习】
一.选择题
1.下列算式中正确的是(
).
A.
B.
C.
D.
2.的结果是(
).
A
.
B.
C.
D.
3.下列各式计算正确的是( )
A.x(x2﹣x﹣1)=x3﹣x﹣1
B.ab(a+b)=a2+b2
C.3x(x2﹣2x﹣1)=3x3﹣6x2﹣3x
D.﹣2x(x2﹣x﹣1)=﹣2x3﹣2x2+2x
4.已知,那么的值为(
).
A.-2
B.2
C.-5
D.5
5.
要使成立,则,的值分别是(
).
A.
B.
C.
D.
6.设M=,N=,则M与N的关系为(
).
A.M<N
B.M>N
C.M=N
D.不能确定
二.填空题
7.
已知三角形的底边为,高是,则三角形的面积是_________.
8.
计算:①=________;②=______;
③=_______;④=______.
9.
方程的解为________.
10.
.
11.
若化简(ax+3y)(x﹣y)的结果中不含xy项,则a的值为
.
12.
若,,则=____________.
三.解答题
14.
解下列各方程.
(1)
(2)
15.
化简求值:
(1),其中.
(2),其中.
要点三、乘法公式
1.平方差公式:
两个数的和与这两个数的差的积,等于这两个数的平方差.
要点诠释:在这里,既可以是具体数字,也可以是单项式或多项式.
平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.
2.
完全平方公式:;
两数和
(差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.
要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍.
【巩固练习】
一.选择题
1.
在下列计算中,不能用平方差公式计算的是(
)
A.
B.
C.
D.
2.若=6,=5,则等于(
).
A.11
B.15
C.30
D.60
3.下列计算正确的是(
).
A.=
B.
=
C.
D.(
)()=
4.下列多项式不是完全平方式的是(
).
A.
B.
C.
D.
5.已知关于x的二次三项式4x2﹣mx+25是完全平方式,则常数m的值为( )
A.10
B.±10
C.﹣20
D.±20
6.下列等式不能恒成立的是(
).
A.
B.
C.
D.
二.填空题
7.若是一个完全平方式,则=______.
8.
若=,则M
=______.
9.
若=3,=1,则=_______.
10.(2015春?陕西校级期末)(1+x)(1﹣x)(1+x2)(1+x4)=
.
11.
___________.
12.若,则代数式的值为________.
三.解答题
13.先化简,再求值:,其中.
14.已知:,且求的值.
要点四、因式分解
把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
因式分解的方法主要有:
提公因式法,
公式法,
分组分解法,
十字相乘法,
添、拆项法等.
要点诠释:落实好方法的综合运用:
首先提取公因式,然后考虑用公式;
两项平方或立方,三项完全或十字;
四项以上想分组,分组分得要合适;
几种方法反复试,最后须是连乘式;
因式分解要彻底,一次一次又一次.
【巩固练习】
一.选择题
1.
下列各式变形中,是因式分解的是(
)
A.
B.
C.
D.
2.
多项式6abc﹣3a2bc+12ab的公因式是( )
A.abc
B.3ab
C.3abc
D.3ab
3.
多项式分解因式的结果是(
)
A.
B.
C.
D.
4.
分解因式的结果是(
)
A.
B.
C.
D.
5.
下列因式分解正确的是(
)
A.
B.
C.
D.
6.
把提公因式得(
)
A.
B.
C.
D.
二.填空题
7.
因式分解是把一个______________化为______________的形式.
8.
的公因式是___________;的公因式是__________.
9.
因式分解=_________________.
10.
多项式的公因式是______________.
11.分解因式:m(x﹣y)+n(y﹣x)=_____________________.
12.
因式分解=_____________________.
三.解答题
13.
应用简便方法计算:
(1);
(2)
14.已知,求和的值.
15.分解因式:6a(b﹣1)﹣2(1﹣b).
PAGE
第1页
