五年级上册数学课件-5.1 平行四边形的面积青岛版 (共31张PPT)
文档属性
| 名称 | 五年级上册数学课件-5.1 平行四边形的面积青岛版 (共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
平行四边形的面积
R·五年级上册
多边形的面积
3.培养学生初步的逻辑思维能力及空间概念,激发学生的创造意识。
1.理解并掌握平行四边形的面积计算公式,会运用计算公式计算平行四边形的面积。
2.能够运用公式解决相应的实际问题。
学习目标
学习重点
学习难点
平行四边形面积公式的推导及应用。
理解平行四边形面积计算公式的推导过程。
一、情景导入
这两个花坛哪一个大呢?
要知道它们的面积……
我只会求长方形的……
这节课我们就来一起学习如何计算平行四边形的面积。
回忆一下,我们是用什么方法得出长方形的面积的计算公式的?
用数方格的方式试一试。
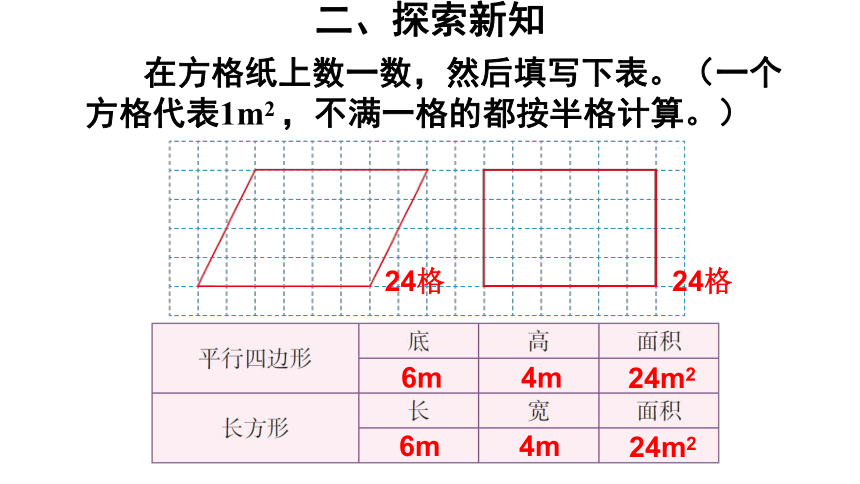
在方格纸上数一数,然后填写下表。(一个方格代表1m2
,不满一格的都按半格计算。)
二、探索新知
24m2
6m
4m
6m
4m
24m2
24格
24格
24m2
6m
4m
6m
4m
24m2
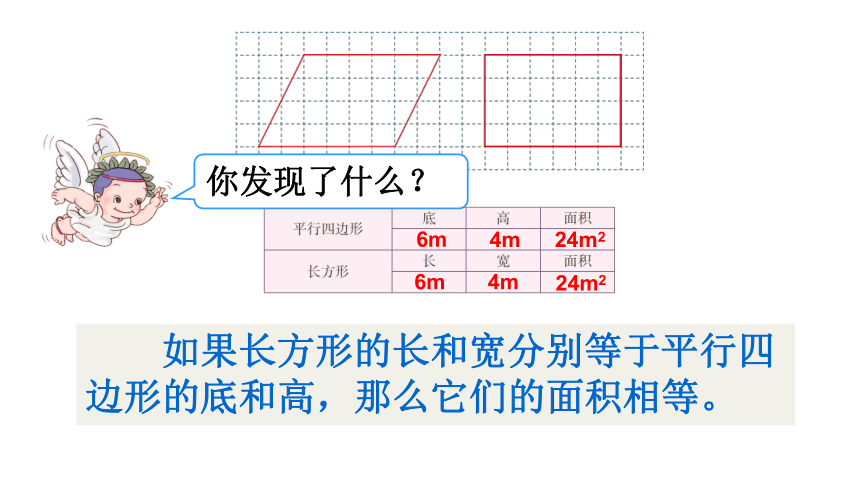
你发现了什么?
如果长方形的长和宽分别等于平行四边形的底和高,那么它们的面积相等。
24m2
6m
4m
6m
4m
24m2
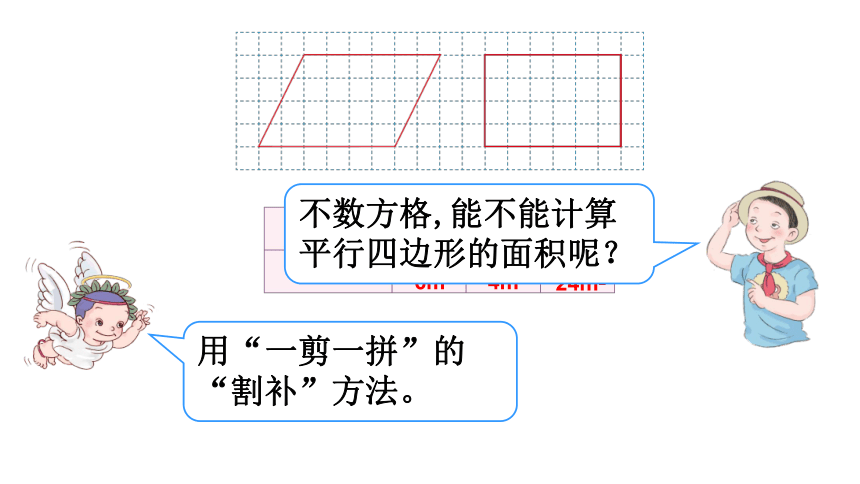
不数方格,能不能计算平行四边形的面积呢?
用“一剪一拼”的
“割补”方法。
可以把平行四边形变成一个长方形。
先沿高剪开,把三角形向右平移,再拼成……
转化成长方形就能计算面积了。
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
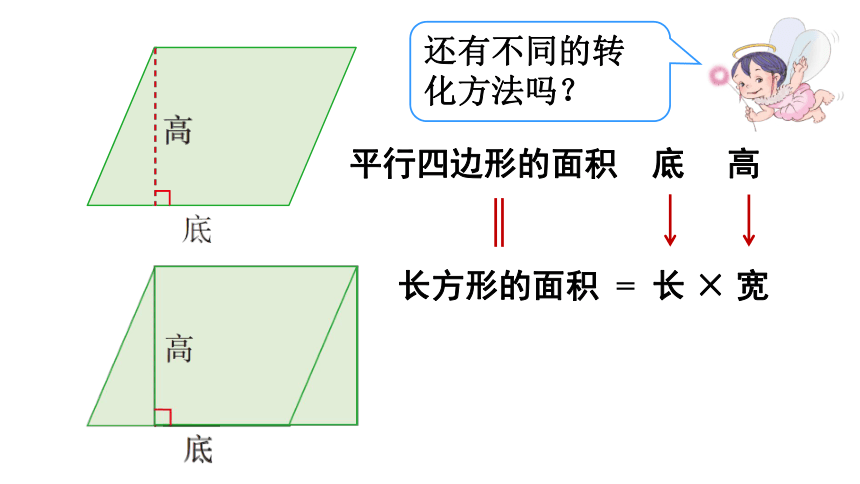
还有不同的转化方法吗?
底
高
底
高
底
高
底
高
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
还有不同的转化方法吗?
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
这两个图形的面积(
)。
平行四边形的底和长方形的(
)相等。
平行四边形的高和长方形的(
)相等。
长
相等
宽
平行四边形的面积
=
_________
底×高
如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,平行四边形的面积计算公式可以写成:S=ah。
回忆一下,刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新)
长方形(旧)
转化(割补)
推导
联系
监控:
平行四边形花坛的底是6m,高是4m,它的面积是多少?
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
三、巩固提高
1.填一填。
(1)把一个长方形木框拉成一个平行四边形,(
)不变,它的高和面积(
)。
(2)平行四边形的高不变,底扩大为原来的2倍,面积(
)。
周长
改变
扩大为原来的2倍
2.计算下面平行四边形的面积。
答:20×13=260(cm2)
3.一块平行四边形的菜地,底是20m,高是16m,若每棵大白菜占地0.16m2,这块地可种多少棵大白菜?
答:这块地可种2000棵大白菜。
20×16÷0.16=2000(棵)
4.一块平行四边形的菜园,底长8.5
m,高6
m,它的面积是多少?
答:8.5×6=51(m2)
5.比较下面两个平行四边形的大小
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
S
=
a
×
h
=
a
·
h
=
ah
四、课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
五、课后作业
六、教学反思
本节课教学我充分让学生自己参与学习,让学生数方格、剪拼,引导学生参与学习全过程,去主动探求知识,强化学生参与意识,我引导学生运用实验割补法把平行四边形转化为长方形,从而找到平行四边形的底与长方形的长的关系,高与宽的关系,根据长方形的面积=长×宽,得到平行四边形面积计算公式是底×高,利用讨论交流等形式要求学生把自己操作——转化——推导的过程叙述出来,以发展学生思维和表达能力。这样教学对于培养学生的空间观念,发展解决生活中实际问题的能力都有重要作用。
平行四边形的面积
R·五年级上册
多边形的面积
3.培养学生初步的逻辑思维能力及空间概念,激发学生的创造意识。
1.理解并掌握平行四边形的面积计算公式,会运用计算公式计算平行四边形的面积。
2.能够运用公式解决相应的实际问题。
学习目标
学习重点
学习难点
平行四边形面积公式的推导及应用。
理解平行四边形面积计算公式的推导过程。
一、情景导入
这两个花坛哪一个大呢?
要知道它们的面积……
我只会求长方形的……
这节课我们就来一起学习如何计算平行四边形的面积。
回忆一下,我们是用什么方法得出长方形的面积的计算公式的?
用数方格的方式试一试。
在方格纸上数一数,然后填写下表。(一个方格代表1m2
,不满一格的都按半格计算。)
二、探索新知
24m2
6m
4m
6m
4m
24m2
24格
24格
24m2
6m
4m
6m
4m
24m2
你发现了什么?
如果长方形的长和宽分别等于平行四边形的底和高,那么它们的面积相等。
24m2
6m
4m
6m
4m
24m2
不数方格,能不能计算平行四边形的面积呢?
用“一剪一拼”的
“割补”方法。
可以把平行四边形变成一个长方形。
先沿高剪开,把三角形向右平移,再拼成……
转化成长方形就能计算面积了。
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
还有不同的转化方法吗?
底
高
底
高
底
高
底
高
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
还有不同的转化方法吗?
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
这两个图形的面积(
)。
平行四边形的底和长方形的(
)相等。
平行四边形的高和长方形的(
)相等。
长
相等
宽
平行四边形的面积
=
_________
底×高
如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,平行四边形的面积计算公式可以写成:S=ah。
回忆一下,刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新)
长方形(旧)
转化(割补)
推导
联系
监控:
平行四边形花坛的底是6m,高是4m,它的面积是多少?
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
三、巩固提高
1.填一填。
(1)把一个长方形木框拉成一个平行四边形,(
)不变,它的高和面积(
)。
(2)平行四边形的高不变,底扩大为原来的2倍,面积(
)。
周长
改变
扩大为原来的2倍
2.计算下面平行四边形的面积。
答:20×13=260(cm2)
3.一块平行四边形的菜地,底是20m,高是16m,若每棵大白菜占地0.16m2,这块地可种多少棵大白菜?
答:这块地可种2000棵大白菜。
20×16÷0.16=2000(棵)
4.一块平行四边形的菜园,底长8.5
m,高6
m,它的面积是多少?
答:8.5×6=51(m2)
5.比较下面两个平行四边形的大小
长方形的面积
=
长
×
宽
平行四边形的面积
底
高
S
=
a
×
h
=
a
·
h
=
ah
四、课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
五、课后作业
六、教学反思
本节课教学我充分让学生自己参与学习,让学生数方格、剪拼,引导学生参与学习全过程,去主动探求知识,强化学生参与意识,我引导学生运用实验割补法把平行四边形转化为长方形,从而找到平行四边形的底与长方形的长的关系,高与宽的关系,根据长方形的面积=长×宽,得到平行四边形面积计算公式是底×高,利用讨论交流等形式要求学生把自己操作——转化——推导的过程叙述出来,以发展学生思维和表达能力。这样教学对于培养学生的空间观念,发展解决生活中实际问题的能力都有重要作用。
