3.2.2 平面直角坐标系(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 3.2.2 平面直角坐标系(知识清单+经典例题+夯实基础+提优特训+中考链接) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第二章位置与坐标
3.2
平面直角坐标系
第二课时
平面直角坐标系(2)
【知识清单】
一、根据坐标找点的方法:
由P(a,b)在x轴上找到坐标为(a,0)的点A,过A作x轴的垂线,再在y轴上找到坐标为
(0,b)的点B,过B作y轴的垂线,两条垂线的交点,即为所找的P点.
二、平面上点坐标与有序实数对的关系:
(1)在直角坐标系中,对于坐标平面内任意一点.都有唯一的一对有序数对(即点的坐标)与它对
应;反过来,对于任意一对有序实数对,都有唯一的一点和它对应.
(2)平面内点的与有序实数对是一一对应的.
(3)平面内点的坐标是有序实数对,当a≠b时,(a,b)和(b,a)是两个不同点的坐标.
三、点到坐标轴及原点的距离点P(x,y)到坐标轴及原点的距离:
(1)点P(x,y)到x轴的距离等于;
(2)点P(x,y)到y轴的距离等于;
(3)点P(x,y)到原点的距离等于.
【经典例题】
【例题】1、如图为A、B、C三点在坐标平面上的位置图.若A、B、C三点横坐标的数字总和为a,y纵坐标的数字总和为b,则点P
(a+b,ab)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【考点】点的坐标.
【分析】先求出A、B、C三点的横坐标的数字和,再求出纵坐标的数字的和,然后把它们相减即可求得a+b,ab之值.
【解答】由图形可得:点A
(1,2)、B
(2,4)、C
(4,3)
∴a=12+4=1,
∴b=2+4+3=5,
∴a+b=1+5=6,
ab=15=4.
∴点P坐标为(6,4)
故选:D.
【点评】考查了点的坐标,根据图形求出三个点横坐标之和a的值和纵坐标之和b的值的解题的关键.
例题2、如图,已知△ABC,请你写出三个顶点的坐标A
(
)、B
(
)
、
C
(
),△ABC的面积等于
.
【考点】三角形的面积;坐标与图形性质.
【分析】如图,根据A、B、C三点所在的位置即可确定其坐标;由A、B的横坐标,容易求得AB的长,以AB为底,过点CD作AB的垂线,垂足为D,所以CD即为AB边上的高,可得点D的坐标为(1,1),则CD的长由C、D两点的纵坐标求得,即可求出△ABC的面积.
【解答】由图形可得A
(2,1),B
(4,1),C
(1,3);
过点C作CD⊥AB于点D,所以CD为AB边上的高,
根据图形,可得D点的坐标为(1,1):
AB=4(2)=6;
边AB上的高
CD=3(1)=4
∴S△ABC=AB?CD
=×6×4=12.
【点评】主要考查了点的坐标的意义以及三角形面积的求法.根据图形得出三角形的底和高的解题的关键.
【夯实基础】
1、如图,一个长方形的长为12,宽为6,分别以两组对边中点的连线为坐标轴建立平面
直角
坐标系,则下列点中不在长方形上的是( )
A.(6,-3)
B.(6,3)
C.(3,6)
D.(0,-3)
2、若一个三角形的三顶点分别为A
(2,4),B
(3,1),C
(5,7),将各顶点的横坐标保持不变,纵坐标都扩大为原来的3倍,那么变化后的三角形的三个顶点坐标分别为( )
A.A
(5,4),B
(6,1),C
(8,7)
B.A
(6,4),B
(9,1),C
(15,7)
C.A
(2,7),B
(3,4),C
(5,10)
D.A
(2,12),B
(3,3),C
(5,21)
3、如图为一个旅游景区停车场的平面部分简图,若“现代”的坐标为(3,2),“奔驰”的坐标
为(1,1),则“宝马”的坐标为( )
A.(2,1)
B.(2,1)
C.(1,2)
D.(1,2)
4、在直角坐标系中,由A
(2,4),B
(6,4),C
(2,2)三点组成的三角形是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
5、(1)
在平面直角坐标系中,点P
(5,12)到原点O的距离是
;
(2)已知点A是纵坐标为8,到原点的距离为17则点A的坐标为
.
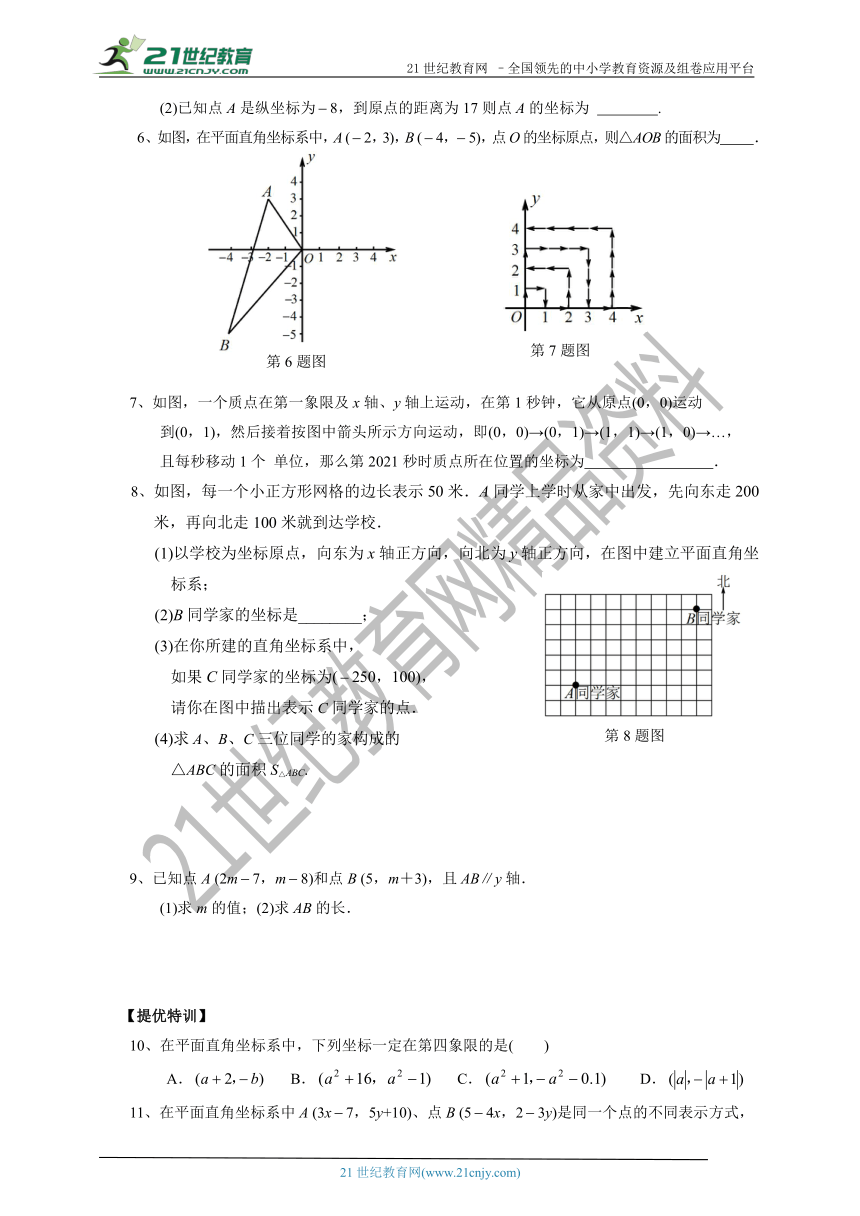
6、如图,在平面直角坐标系中,A
(2,3),B
(4,5),点O的坐标原点,则△AOB的面积为
.
7、如图,一个质点在第一象限及x轴、y轴上运动,在第1秒钟,它从原点(0,0)运动
到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,
且每秒移动1个
单位,那么第2021秒时质点所在位置的坐标为
.
8、如图,每一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走200米,再向北走100米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐
标系;
(2)B同学家的坐标是________;
(3)在你所建的直角坐标系中,
如果C同学家的坐标为(250,100),
请你在图中描出表示C同学家的点.
(4)求A、B、C三位同学的家构成的
△ABC的面积S△ABC.
9、已知点A
(2m7,m8)和点B
(5,m+3),且AB∥y轴.
(1)求m的值;(2)求AB的长.
【提优特训】
10、在平面直角坐标系中,下列坐标一定在第四象限的是( )
A.
B.
C.
D.
11、在平面直角坐标系中A
(3x7,5y+10)、点B
(54x,23y)是同一个点的不同表示方式,
则P
(x,y)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
12、在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(1,1)、
(1,1)、(1,1),则顶点D的坐标为(
)
A.(1,1)??
B.(1,
1)??
C.(1,1)???
?D.(1,1)
13、在平面直角坐标系中,已知点A(7,0),点B(5,0),点C在y轴上,三角形ABC的
面积为18,则点C的坐标为
(0,3)或(0,3)
.
A.(0,3)??
B.(0,
3)??
C.(0,3)?或(0,
3)?
?D.(3,0)?或(3,0)
14、以点P(3,0)为圆心,以5为半径画圆,分别交x轴于点M,N,交y轴于点P,Q,
则四边形MPQN的周长是
,面积为
.
15、如图,△ABC,点A的坐标为(0,2),点C的坐标为(6,5),要使△ABD≌△ABC,那么
点D的坐标是
.
16、在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2021的坐标是
.
17、在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值;“铅垂高”h:任意两点纵坐标差的最大值;则“矩面积”S=ah.
例如:三点坐标分别为A
(2,3),B
(4,1),C
(3,2),则“水平底”a=7,“矩面积”h=5,“矩面积”S=ah=35.
已知点A
(3,7),B
(5,6),P
(0,t).(1)若A,B,P三点的“矩面积”为32,求点P的坐标;(2)直接写出A,B,P三点的“矩面积”的最小值.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0,
y1),B2(0,
y2),Q(x2,
y1).
因为,,
所以Rt△P1P2
Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A
(3,4),B
(5,10),求AB的距离;
(2)若平面三点A
(2,2),B
(5,2),C
(1,4),试判定△ABC的形状,说明理由.
【中考链接】
19、(2019?湖南株洲)
在平面直角坐标系中,点A
(2,3)位于哪个象限(
)
A.第一象限??
B.第二象限??
C.第三象限??
?D.第四象限
20、(2019?甘肃)
已知点P
(m+2,2m4)在x轴上,则点P的坐标为(
)
A.(4,0)?
B.(0,4)??
C.(4,0)??
?D.(0,4)
参考答案
1、C
2、D
3、B
4、C
5、(1)13、(2)±
15
6、11
7、(3,44)
10、C
11、B
12、D
13、C
14、
、40
15、(6,1)或(2,5)
或(6,1)
16、19、D
20、A
8、如图,每一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走200米,再向北走100米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐
标系;
(2)B同学家的坐标是________;
(3)在你所建的直角坐标系中,
如果C同学家的坐标为(250,100),
请你在图中描出表示C同学家的点.
(4)求A、B、C三位同学的家构成的
△ABC的面积S△ABC.
解:(1)平面直角坐标系如图所示.
(2)(200,150)
(3)C同学家的位置如图所示.
(4)S△ABC=(5×50)×(9×50)×(8×50)×(5×50)
×(9×50)×(1×50)×(5×50)×(1×50)
=45000(米)2.
所以A、B、C三位同学的家构成的△ABC的面积S△ABC为45000平方米.
9、已知点A
(2m7,m8)和点B
(5,m+3),且AB∥y轴.
(1)求m的值;
(2)求AB的长.
解:(1)因为点A的坐标为(2m7,m8),点B的坐标为(5,m+3),且AB∥y轴,
所以2m7=5,所以m=6.
(2)由(1)可知m=6,所以m8=2,m+3=9,
所以点A的坐标为(5,2),点B的坐标为(5,9).
∵AB的长就是A、B两点纵坐标的差的绝对值,
即9(2)=11,所以AB的长为11.
17、在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值;“铅垂高”h:任意两点纵坐标差的最大值;则“矩面积”S=ah.
例如:三点坐标分别为A
(2,3),B
(4,1),C
(3,2),则“水平底”a=7,“矩面积”h=5,“矩面积”S=ah=35.
已知点A
(3,7),B
(5,6),P
(0,t).(1)若A,B,P三点的“矩面积”为32,求点P的坐标;(2)直接写出A,B,P三点的“矩面积”的最小值.
解:(1)由题意:“水平底”a=3(5)=8,
当t>7时,“铅垂高”h
=t6,
则“矩面积”S=ah
=8(t6)=32,
解得t=10,
故点P的坐标为(0,10);
当t<6时,“铅垂高”h
=7t,
则“矩面积”S=ah
=8(7t)=32,
解得t=3,
故点P的坐标为(0,
3),
所以,点P的坐标为(0,10)或(0,3);
(2)∵a=8,
∴t=6或7时,“铅垂高”h最小为1,
此时,A,B,P三点的“矩面积”的最小值为8.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0,
y1),B2(0,
y2),Q(x2,
y1).
因为,,
所以Rt△P1P2
Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A
(3,4),B
(5,10),求AB的距离;
(2)若平面三点A
(2,2),B
(5,2),C
(1,4),试判定△ABC的形状,说明理由.
解:(1)∵A
(3,4),B
(5,10),
由两点间的距离公式,得
∴
.
(2)∵A
(2,2),B
(5,2),C
(1,4),
由两点间的距离公式,得
∴,
∴,
∴
∵,.
∴
∴△ABC是直角三角形.
第16题图
第15题图
第3题图
第7题图
第18题图
第1题图
第16题图
第6题图
第8题图
例题1图
第8题图
例题2图
第8题图
第18题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第二章位置与坐标
3.2
平面直角坐标系
第二课时
平面直角坐标系(2)
【知识清单】
一、根据坐标找点的方法:
由P(a,b)在x轴上找到坐标为(a,0)的点A,过A作x轴的垂线,再在y轴上找到坐标为
(0,b)的点B,过B作y轴的垂线,两条垂线的交点,即为所找的P点.
二、平面上点坐标与有序实数对的关系:
(1)在直角坐标系中,对于坐标平面内任意一点.都有唯一的一对有序数对(即点的坐标)与它对
应;反过来,对于任意一对有序实数对,都有唯一的一点和它对应.
(2)平面内点的与有序实数对是一一对应的.
(3)平面内点的坐标是有序实数对,当a≠b时,(a,b)和(b,a)是两个不同点的坐标.
三、点到坐标轴及原点的距离点P(x,y)到坐标轴及原点的距离:
(1)点P(x,y)到x轴的距离等于;
(2)点P(x,y)到y轴的距离等于;
(3)点P(x,y)到原点的距离等于.
【经典例题】
【例题】1、如图为A、B、C三点在坐标平面上的位置图.若A、B、C三点横坐标的数字总和为a,y纵坐标的数字总和为b,则点P
(a+b,ab)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【考点】点的坐标.
【分析】先求出A、B、C三点的横坐标的数字和,再求出纵坐标的数字的和,然后把它们相减即可求得a+b,ab之值.
【解答】由图形可得:点A
(1,2)、B
(2,4)、C
(4,3)
∴a=12+4=1,
∴b=2+4+3=5,
∴a+b=1+5=6,
ab=15=4.
∴点P坐标为(6,4)
故选:D.
【点评】考查了点的坐标,根据图形求出三个点横坐标之和a的值和纵坐标之和b的值的解题的关键.
例题2、如图,已知△ABC,请你写出三个顶点的坐标A
(
)、B
(
)
、
C
(
),△ABC的面积等于
.
【考点】三角形的面积;坐标与图形性质.
【分析】如图,根据A、B、C三点所在的位置即可确定其坐标;由A、B的横坐标,容易求得AB的长,以AB为底,过点CD作AB的垂线,垂足为D,所以CD即为AB边上的高,可得点D的坐标为(1,1),则CD的长由C、D两点的纵坐标求得,即可求出△ABC的面积.
【解答】由图形可得A
(2,1),B
(4,1),C
(1,3);
过点C作CD⊥AB于点D,所以CD为AB边上的高,
根据图形,可得D点的坐标为(1,1):
AB=4(2)=6;
边AB上的高
CD=3(1)=4
∴S△ABC=AB?CD
=×6×4=12.
【点评】主要考查了点的坐标的意义以及三角形面积的求法.根据图形得出三角形的底和高的解题的关键.
【夯实基础】
1、如图,一个长方形的长为12,宽为6,分别以两组对边中点的连线为坐标轴建立平面
直角
坐标系,则下列点中不在长方形上的是( )
A.(6,-3)
B.(6,3)
C.(3,6)
D.(0,-3)
2、若一个三角形的三顶点分别为A
(2,4),B
(3,1),C
(5,7),将各顶点的横坐标保持不变,纵坐标都扩大为原来的3倍,那么变化后的三角形的三个顶点坐标分别为( )
A.A
(5,4),B
(6,1),C
(8,7)
B.A
(6,4),B
(9,1),C
(15,7)
C.A
(2,7),B
(3,4),C
(5,10)
D.A
(2,12),B
(3,3),C
(5,21)
3、如图为一个旅游景区停车场的平面部分简图,若“现代”的坐标为(3,2),“奔驰”的坐标
为(1,1),则“宝马”的坐标为( )
A.(2,1)
B.(2,1)
C.(1,2)
D.(1,2)
4、在直角坐标系中,由A
(2,4),B
(6,4),C
(2,2)三点组成的三角形是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
5、(1)
在平面直角坐标系中,点P
(5,12)到原点O的距离是
;
(2)已知点A是纵坐标为8,到原点的距离为17则点A的坐标为
.
6、如图,在平面直角坐标系中,A
(2,3),B
(4,5),点O的坐标原点,则△AOB的面积为
.
7、如图,一个质点在第一象限及x轴、y轴上运动,在第1秒钟,它从原点(0,0)运动
到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,
且每秒移动1个
单位,那么第2021秒时质点所在位置的坐标为
.
8、如图,每一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走200米,再向北走100米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐
标系;
(2)B同学家的坐标是________;
(3)在你所建的直角坐标系中,
如果C同学家的坐标为(250,100),
请你在图中描出表示C同学家的点.
(4)求A、B、C三位同学的家构成的
△ABC的面积S△ABC.
9、已知点A
(2m7,m8)和点B
(5,m+3),且AB∥y轴.
(1)求m的值;(2)求AB的长.
【提优特训】
10、在平面直角坐标系中,下列坐标一定在第四象限的是( )
A.
B.
C.
D.
11、在平面直角坐标系中A
(3x7,5y+10)、点B
(54x,23y)是同一个点的不同表示方式,
则P
(x,y)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
12、在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(1,1)、
(1,1)、(1,1),则顶点D的坐标为(
)
A.(1,1)??
B.(1,
1)??
C.(1,1)???
?D.(1,1)
13、在平面直角坐标系中,已知点A(7,0),点B(5,0),点C在y轴上,三角形ABC的
面积为18,则点C的坐标为
(0,3)或(0,3)
.
A.(0,3)??
B.(0,
3)??
C.(0,3)?或(0,
3)?
?D.(3,0)?或(3,0)
14、以点P(3,0)为圆心,以5为半径画圆,分别交x轴于点M,N,交y轴于点P,Q,
则四边形MPQN的周长是
,面积为
.
15、如图,△ABC,点A的坐标为(0,2),点C的坐标为(6,5),要使△ABD≌△ABC,那么
点D的坐标是
.
16、在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2021的坐标是
.
17、在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值;“铅垂高”h:任意两点纵坐标差的最大值;则“矩面积”S=ah.
例如:三点坐标分别为A
(2,3),B
(4,1),C
(3,2),则“水平底”a=7,“矩面积”h=5,“矩面积”S=ah=35.
已知点A
(3,7),B
(5,6),P
(0,t).(1)若A,B,P三点的“矩面积”为32,求点P的坐标;(2)直接写出A,B,P三点的“矩面积”的最小值.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0,
y1),B2(0,
y2),Q(x2,
y1).
因为,,
所以Rt△P1P2
Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A
(3,4),B
(5,10),求AB的距离;
(2)若平面三点A
(2,2),B
(5,2),C
(1,4),试判定△ABC的形状,说明理由.
【中考链接】
19、(2019?湖南株洲)
在平面直角坐标系中,点A
(2,3)位于哪个象限(
)
A.第一象限??
B.第二象限??
C.第三象限??
?D.第四象限
20、(2019?甘肃)
已知点P
(m+2,2m4)在x轴上,则点P的坐标为(
)
A.(4,0)?
B.(0,4)??
C.(4,0)??
?D.(0,4)
参考答案
1、C
2、D
3、B
4、C
5、(1)13、(2)±
15
6、11
7、(3,44)
10、C
11、B
12、D
13、C
14、
、40
15、(6,1)或(2,5)
或(6,1)
16、19、D
20、A
8、如图,每一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走200米,再向北走100米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐
标系;
(2)B同学家的坐标是________;
(3)在你所建的直角坐标系中,
如果C同学家的坐标为(250,100),
请你在图中描出表示C同学家的点.
(4)求A、B、C三位同学的家构成的
△ABC的面积S△ABC.
解:(1)平面直角坐标系如图所示.
(2)(200,150)
(3)C同学家的位置如图所示.
(4)S△ABC=(5×50)×(9×50)×(8×50)×(5×50)
×(9×50)×(1×50)×(5×50)×(1×50)
=45000(米)2.
所以A、B、C三位同学的家构成的△ABC的面积S△ABC为45000平方米.
9、已知点A
(2m7,m8)和点B
(5,m+3),且AB∥y轴.
(1)求m的值;
(2)求AB的长.
解:(1)因为点A的坐标为(2m7,m8),点B的坐标为(5,m+3),且AB∥y轴,
所以2m7=5,所以m=6.
(2)由(1)可知m=6,所以m8=2,m+3=9,
所以点A的坐标为(5,2),点B的坐标为(5,9).
∵AB的长就是A、B两点纵坐标的差的绝对值,
即9(2)=11,所以AB的长为11.
17、在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值;“铅垂高”h:任意两点纵坐标差的最大值;则“矩面积”S=ah.
例如:三点坐标分别为A
(2,3),B
(4,1),C
(3,2),则“水平底”a=7,“矩面积”h=5,“矩面积”S=ah=35.
已知点A
(3,7),B
(5,6),P
(0,t).(1)若A,B,P三点的“矩面积”为32,求点P的坐标;(2)直接写出A,B,P三点的“矩面积”的最小值.
解:(1)由题意:“水平底”a=3(5)=8,
当t>7时,“铅垂高”h
=t6,
则“矩面积”S=ah
=8(t6)=32,
解得t=10,
故点P的坐标为(0,10);
当t<6时,“铅垂高”h
=7t,
则“矩面积”S=ah
=8(7t)=32,
解得t=3,
故点P的坐标为(0,
3),
所以,点P的坐标为(0,10)或(0,3);
(2)∵a=8,
∴t=6或7时,“铅垂高”h最小为1,
此时,A,B,P三点的“矩面积”的最小值为8.
18、先阅读理解下面的问题,再按要求解答问题:
如图,在平面直角坐标系中,已知两点,,如何求P1P2的距离.
若,,过P1,P2分别向x轴,y轴作垂线.垂足分别为A1(x1,0),A2(x2,0),B1(0,
y1),B2(0,
y2),Q(x2,
y1).
因为,,
所以Rt△P1P2
Q中,
,
所以.
因此,我们得到平面上两点,
之间的距离公式为.
根据上面得到的公式,解决下列问题:
(1)已知平面两点A
(3,4),B
(5,10),求AB的距离;
(2)若平面三点A
(2,2),B
(5,2),C
(1,4),试判定△ABC的形状,说明理由.
解:(1)∵A
(3,4),B
(5,10),
由两点间的距离公式,得
∴
.
(2)∵A
(2,2),B
(5,2),C
(1,4),
由两点间的距离公式,得
∴,
∴,
∴
∵,.
∴
∴△ABC是直角三角形.
第16题图
第15题图
第3题图
第7题图
第18题图
第1题图
第16题图
第6题图
第8题图
例题1图
第8题图
例题2图
第8题图
第18题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
