高中数学人教B版选修2-1第一章 1.2.1 “且”与“或”(共21张PPT)
文档属性
| 名称 | 高中数学人教B版选修2-1第一章 1.2.1 “且”与“或”(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 20:05:27 | ||
图片预览








文档简介
(共21张PPT)
1.2.1“且”与“或”
学习目标
1.通过数学实例了解“且”与“或”的含义
2.能判定由“且”与“或”组成的新命题的真假
3.通过学习“且”与“或”,体会逻辑在表述和论证中的作用
思考1:
下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除.
简单命题
简单命题
复合命题
思考2:
对于命题“矩形的对角线相等”和“矩形的对角线互相平分”,用联结词“且”联结这两个命题,得到的新命题是什么?
矩形的对角线相等且互相平分.
一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,
记作
p∧q
读作
p且q
练习1
将下列命题用“且”联结成新命题
(1)
p
:平行四边形的对角线互相平分,
q
:平行四边形的对角线相等;
(2)
p
:菱形的对角线互相垂直,
q
:菱形的对角线互相平分;
(3)
p
:35是15的倍数,
q
:35是7的倍数。
解:p
∧q
:
平行四边形的对角线互相平分且相等。
解:
p∧q
:
菱形的对角线互相垂直且平分。
解:
p∧q
:
35是15的倍数且是7的倍数。
探究p且q的真假
思考3:
“且”
相当于集合A与集合B的(
)集?
交
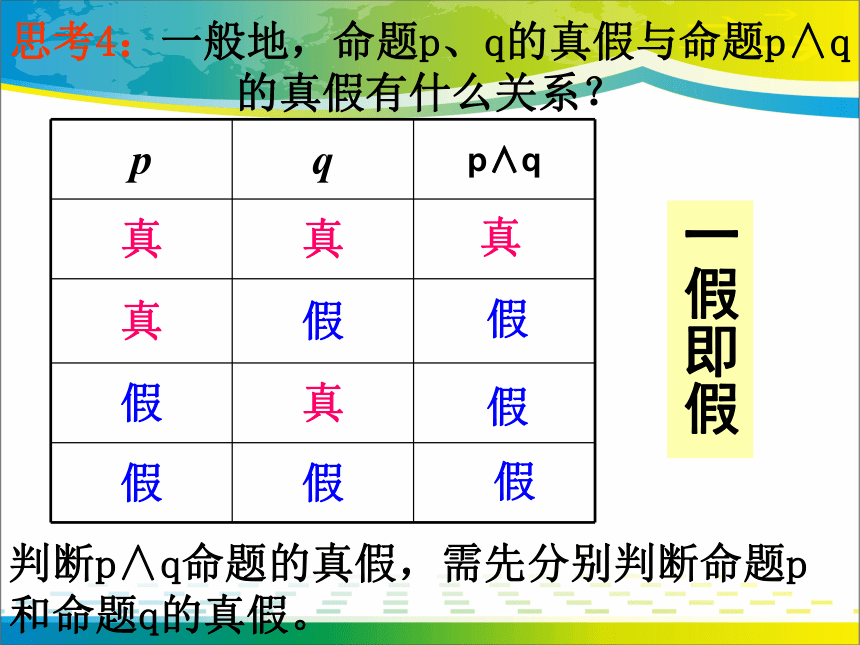
思考4:一般地,命题p、q的真假与命题p∧q的真假有什么关系?
一假即假
真
假
假
假
判断p∧q命题的真假,需先分别判断命题p和命题q的真假。
p
q
p∧q
真
真
真
假
假
真
假
假
例1:将下列命题用“且”联结成新命题,并判断它们的真假。
(1)
p
:平行四边形的对角线互相平分,
q
:平行四边形的对角线相等;
(2)
p
:菱形的对角线互相垂直,
q
:菱形的对角线互相平分;
(3)
p
:35是15的倍数,
q
:35是7的倍数。
解:
p
∧q
:
平行四边形的对角线互相平分且相等。
解:
p∧q
:
菱形的对角线互相垂直且平分。
解:
p∧q
:
35是15的倍数且是7的倍数。
∵
p是真命题,
q是假命题,∴p∧q是假命题.
∵p、q都是真命题,
∴
p∧q是真命题.
∵
p是假命题,
q是真命题,∴
p∧q是假命题
练习2:用“且”联结下列各组命题组成新命题,并分别判断它们的真假:
(1)p真q真
p∧q真
(2)p真q真
p∧q真
(3)p真q真
p∧q真
(4)p真q假
p∧q假
(5)p假q真
p∧q假
思考5:
下列三个命题间有什么关系?
(1)27是9的倍数;
(2)27是7的倍数;
(3)27是9的倍数或是7的倍数;
简单命题
简单命题
复合命题
一般地,用逻辑联结词“或”把命题p和命题q联结起来,
就得到一个新命题,
记作
p∨q,
读作
p或q
练习3:将下列命题用“或”联结成一个新命题
(1)p:12能被3整除;
q:12能被4整除;
(2)P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
(3)p:6是奇数;
q:6是质数;
p∨q:12能被3整除或能被4整除;
p∨q:等腰三角形两腰相等或三条中线相等.
p∨q:6是奇数或是质数.
探究p或q的真假
思考6:
“或”
相当于集合A与集合B的(
)集?
并
一真即真
思考7:一般地,命题p、q的真假与命题p∨q的真假有什么关系?
真
真
真
假
判断p∨q命题的真假,需先分别判断命题p和命题q的真假。
p
q
p∨q
真
真
真
假
假
真
假
假
例2:将下列命题用“或”联结成新命题,并判断它们的真假
(1)p:12能被3整除;
q:12能被4整除;
p∨q:12能被3整除或能被4整除;
(2)P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∨q:等腰三角形两腰相等或三条中线相等.
(3)p:6是奇数;
q:6是质数;
p∨q:6是奇数或是质数.
∵
p是真命题,
q是真命题,∴
p∨q是真命题.
∵
p是真命题,
q是假命题,∴
p∨q是真命题.
∵
p是假命题,
q是假命题,∴
p∨q是假命题.
练习4:用“或”联结下列各组命题组成新命题,并分别判断它们的真假:
(1)p真q真
p∨q真
(2)p真q假
p∨q真
(3)p真q假
p∨q真
(4)p假q假
p∨q假
(5)p真q假
p∨q真
练习6:在下列命题中
(1)命题“不等式
,没有实数解”;
(2)命题“1是偶数或奇数”;
(3)命题“
既属于集合
,也属于集合
”;
(4)命题“
”
其中,真命题为_____________.
(2)(4)
(1)p、q全是真命题。
(2)p、q至少一个是假命题。
(3)p、q至少一个是真命题。
(4)p、q全是假命题。
本课小结:
复合命题p∧q
(p且q)真假判断:
复合命题p∨q(p或q)真假判断:
一真即真
一假即假
1.2.1“且”与“或”
学习目标
1.通过数学实例了解“且”与“或”的含义
2.能判定由“且”与“或”组成的新命题的真假
3.通过学习“且”与“或”,体会逻辑在表述和论证中的作用
思考1:
下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除.
简单命题
简单命题
复合命题
思考2:
对于命题“矩形的对角线相等”和“矩形的对角线互相平分”,用联结词“且”联结这两个命题,得到的新命题是什么?
矩形的对角线相等且互相平分.
一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,
记作
p∧q
读作
p且q
练习1
将下列命题用“且”联结成新命题
(1)
p
:平行四边形的对角线互相平分,
q
:平行四边形的对角线相等;
(2)
p
:菱形的对角线互相垂直,
q
:菱形的对角线互相平分;
(3)
p
:35是15的倍数,
q
:35是7的倍数。
解:p
∧q
:
平行四边形的对角线互相平分且相等。
解:
p∧q
:
菱形的对角线互相垂直且平分。
解:
p∧q
:
35是15的倍数且是7的倍数。
探究p且q的真假
思考3:
“且”
相当于集合A与集合B的(
)集?
交
思考4:一般地,命题p、q的真假与命题p∧q的真假有什么关系?
一假即假
真
假
假
假
判断p∧q命题的真假,需先分别判断命题p和命题q的真假。
p
q
p∧q
真
真
真
假
假
真
假
假
例1:将下列命题用“且”联结成新命题,并判断它们的真假。
(1)
p
:平行四边形的对角线互相平分,
q
:平行四边形的对角线相等;
(2)
p
:菱形的对角线互相垂直,
q
:菱形的对角线互相平分;
(3)
p
:35是15的倍数,
q
:35是7的倍数。
解:
p
∧q
:
平行四边形的对角线互相平分且相等。
解:
p∧q
:
菱形的对角线互相垂直且平分。
解:
p∧q
:
35是15的倍数且是7的倍数。
∵
p是真命题,
q是假命题,∴p∧q是假命题.
∵p、q都是真命题,
∴
p∧q是真命题.
∵
p是假命题,
q是真命题,∴
p∧q是假命题
练习2:用“且”联结下列各组命题组成新命题,并分别判断它们的真假:
(1)p真q真
p∧q真
(2)p真q真
p∧q真
(3)p真q真
p∧q真
(4)p真q假
p∧q假
(5)p假q真
p∧q假
思考5:
下列三个命题间有什么关系?
(1)27是9的倍数;
(2)27是7的倍数;
(3)27是9的倍数或是7的倍数;
简单命题
简单命题
复合命题
一般地,用逻辑联结词“或”把命题p和命题q联结起来,
就得到一个新命题,
记作
p∨q,
读作
p或q
练习3:将下列命题用“或”联结成一个新命题
(1)p:12能被3整除;
q:12能被4整除;
(2)P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
(3)p:6是奇数;
q:6是质数;
p∨q:12能被3整除或能被4整除;
p∨q:等腰三角形两腰相等或三条中线相等.
p∨q:6是奇数或是质数.
探究p或q的真假
思考6:
“或”
相当于集合A与集合B的(
)集?
并
一真即真
思考7:一般地,命题p、q的真假与命题p∨q的真假有什么关系?
真
真
真
假
判断p∨q命题的真假,需先分别判断命题p和命题q的真假。
p
q
p∨q
真
真
真
假
假
真
假
假
例2:将下列命题用“或”联结成新命题,并判断它们的真假
(1)p:12能被3整除;
q:12能被4整除;
p∨q:12能被3整除或能被4整除;
(2)P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∨q:等腰三角形两腰相等或三条中线相等.
(3)p:6是奇数;
q:6是质数;
p∨q:6是奇数或是质数.
∵
p是真命题,
q是真命题,∴
p∨q是真命题.
∵
p是真命题,
q是假命题,∴
p∨q是真命题.
∵
p是假命题,
q是假命题,∴
p∨q是假命题.
练习4:用“或”联结下列各组命题组成新命题,并分别判断它们的真假:
(1)p真q真
p∨q真
(2)p真q假
p∨q真
(3)p真q假
p∨q真
(4)p假q假
p∨q假
(5)p真q假
p∨q真
练习6:在下列命题中
(1)命题“不等式
,没有实数解”;
(2)命题“1是偶数或奇数”;
(3)命题“
既属于集合
,也属于集合
”;
(4)命题“
”
其中,真命题为_____________.
(2)(4)
(1)p、q全是真命题。
(2)p、q至少一个是假命题。
(3)p、q至少一个是真命题。
(4)p、q全是假命题。
本课小结:
复合命题p∧q
(p且q)真假判断:
复合命题p∨q(p或q)真假判断:
一真即真
一假即假
