高中数学人教版必修5课件:2.5等比数列的前n项和(共21张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:2.5等比数列的前n项和(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 20:07:28 | ||
图片预览







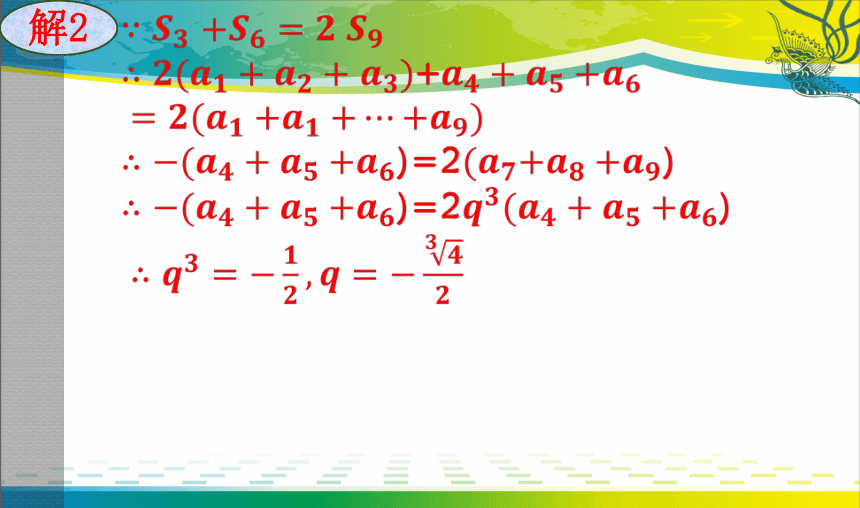

文档简介
(共21张PPT)
2.5等比数列
的前n项和
问题1
问题预习
问题2
首项、公比、项数分别为1,2,64
问题3
问题4
在这个算中,
两边同乘以2,“2”在这个数列中
是一个什么角色?
两边同乘以2,即两边同乘以公比2,使原数列的各项相应增加1次,两式相减时,就有许多项可以抵消.这种方法称“错位相减法”
问题5
问题6
问题7
问题8
题型1
例1
解
例2
解1
解2
作业布置
课本P61
A组
1,2,3,4,5
题型2
例3
解1
解2
数列的求和方法的类型
类型1
公式法
公式法常与其它方法相结合使用,单独命题并不多见
类型2
错位相减法
例4
解
类型3
裂项相消法
例5
解
并项求和法
类型4
直接把求和的项按加法结合律两两结合(或三三
结合)求和
例6
解
类型5
分组求和法
把数列的每一项分成若干部分,并分别的把具有相同特征的部分放到一起,使其转化为前面的类型数列求和.
⊙
阅读教材P55的故事,思考第64个格子应放
多少粒小麦?棋盘上共有多少麦粒?假定1
千粒小麦的质量为40g而目前世界年度小
麦产量约为6亿t你认为国王是否能满足他
的要求吗?
2
63
2
64
他们是怎样算出棋盘上的麦粒数是264-1
的呢?棋盘上的麦粒数依次为:1,2,4,;8,…,263,
这个数列是一个什么数列?其首项、公比、
项数分别为多少?
(264-1)×1019,总质量
超过7000亿吨
64=1+2+22+23+…+263…①
由于2的次数依次递增,所以两边乘以得
2S64=2+22+23+24…+26…②
比较两个式子,你发现两边有什么到吗?
为了求S64,我们应怎样处理它?
两边有2,2223,24…,263完全相同①-②得
S64=1-2
64
64
=264-1
你能用上述方法“错位相减法”去求等比数列
的前n项和Sn=a1+a1q+a1q2+…+
a1q-1(q≠1)吗
n=a1+a1q+a1q2+…+a1qn-1……①
Sn=a19+a19+a1g+.+a1g
2
①-②得:(1-q)Sn=a1-a1qn
q≠1
a1(1-q
若q=1等比数列的前n项和Sn=a1+
a1q+a1q2+…+a1q-1又怎样求呢?
sm=na1
a1(1-q2)
等比数列的前原n=1q(q≠1)
na1(q=1)
能用an、a1、q来表示等比数列的前项和Sn?
2.5等比数列
的前n项和
问题1
问题预习
问题2
首项、公比、项数分别为1,2,64
问题3
问题4
在这个算中,
两边同乘以2,“2”在这个数列中
是一个什么角色?
两边同乘以2,即两边同乘以公比2,使原数列的各项相应增加1次,两式相减时,就有许多项可以抵消.这种方法称“错位相减法”
问题5
问题6
问题7
问题8
题型1
例1
解
例2
解1
解2
作业布置
课本P61
A组
1,2,3,4,5
题型2
例3
解1
解2
数列的求和方法的类型
类型1
公式法
公式法常与其它方法相结合使用,单独命题并不多见
类型2
错位相减法
例4
解
类型3
裂项相消法
例5
解
并项求和法
类型4
直接把求和的项按加法结合律两两结合(或三三
结合)求和
例6
解
类型5
分组求和法
把数列的每一项分成若干部分,并分别的把具有相同特征的部分放到一起,使其转化为前面的类型数列求和.
⊙
阅读教材P55的故事,思考第64个格子应放
多少粒小麦?棋盘上共有多少麦粒?假定1
千粒小麦的质量为40g而目前世界年度小
麦产量约为6亿t你认为国王是否能满足他
的要求吗?
2
63
2
64
他们是怎样算出棋盘上的麦粒数是264-1
的呢?棋盘上的麦粒数依次为:1,2,4,;8,…,263,
这个数列是一个什么数列?其首项、公比、
项数分别为多少?
(264-1)×1019,总质量
超过7000亿吨
64=1+2+22+23+…+263…①
由于2的次数依次递增,所以两边乘以得
2S64=2+22+23+24…+26…②
比较两个式子,你发现两边有什么到吗?
为了求S64,我们应怎样处理它?
两边有2,2223,24…,263完全相同①-②得
S64=1-2
64
64
=264-1
你能用上述方法“错位相减法”去求等比数列
的前n项和Sn=a1+a1q+a1q2+…+
a1q-1(q≠1)吗
n=a1+a1q+a1q2+…+a1qn-1……①
Sn=a19+a19+a1g+.+a1g
2
①-②得:(1-q)Sn=a1-a1qn
q≠1
a1(1-q
若q=1等比数列的前n项和Sn=a1+
a1q+a1q2+…+a1q-1又怎样求呢?
sm=na1
a1(1-q2)
等比数列的前原n=1q(q≠1)
na1(q=1)
能用an、a1、q来表示等比数列的前项和Sn?
