北师大版数学五年级上册 4.4 探究活动:三角形的面积 课件(22张ppt)
文档属性
| 名称 | 北师大版数学五年级上册 4.4 探究活动:三角形的面积 课件(22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 935.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 19:12:35 | ||
图片预览






文档简介
第四单元 多边形的面积
第 4 课时
探究活动:
三角形的面积
在实际情景中,认识计算三角形面积的必要性。
在自主探索中,经历推导三角形面积计算公式的过程,渗透转化思想。
能运用三角形的面积公式计算相关图形的面积,解决实际问题。(重点)
理解拼成的平行四边形和原来的三角形的关系。
(难点)
回顾前面所学知识,完成下列填空。
(1)把一个平行四边形,沿着高剪成两部分,平移
后可得到一个( )形,它的长相当于平行
四边形的( ),它的宽相当于平行四边形
的( )。
(2)平行四边形的底是 6 cm,高是 5 cm,面积是
( )cm?。
长方
底
高
30
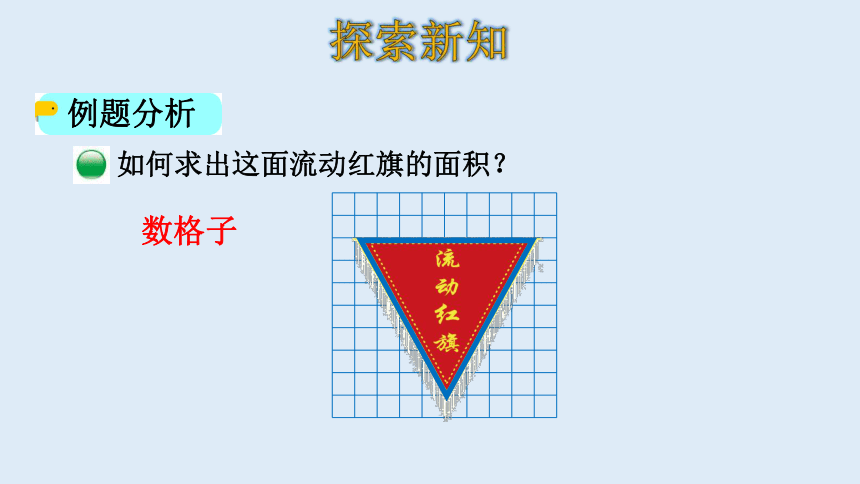
例题分析
如何求出这面流动红旗的面积?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数格子
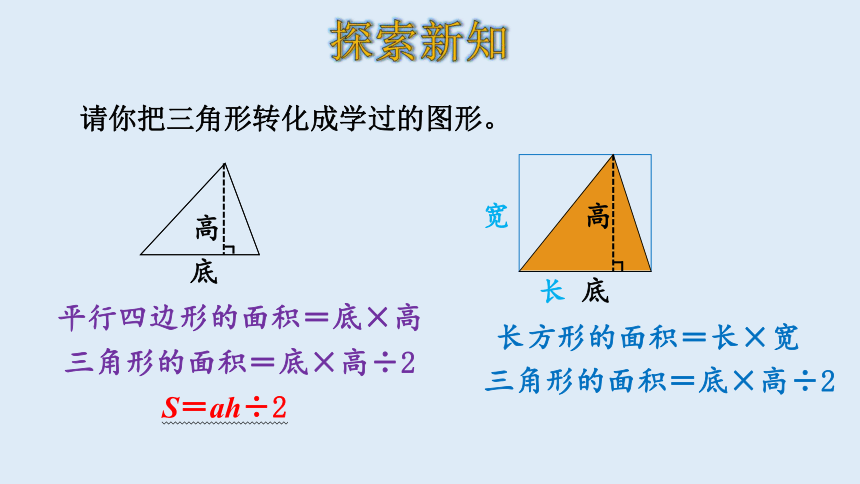
请你把三角形转化成学过的图形。
底
高
底
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
长方形的面积=长×宽
三角形的面积=底×高÷2
长
宽
S=ah÷2
28cm
25cm
三角形的面积=底×高÷2
=28×25÷2
你能求出这面流动红旗的面积吗?
=350(cm?)
知识提炼
知识点:
三角形的面积=底×高÷2
S=ah÷2。
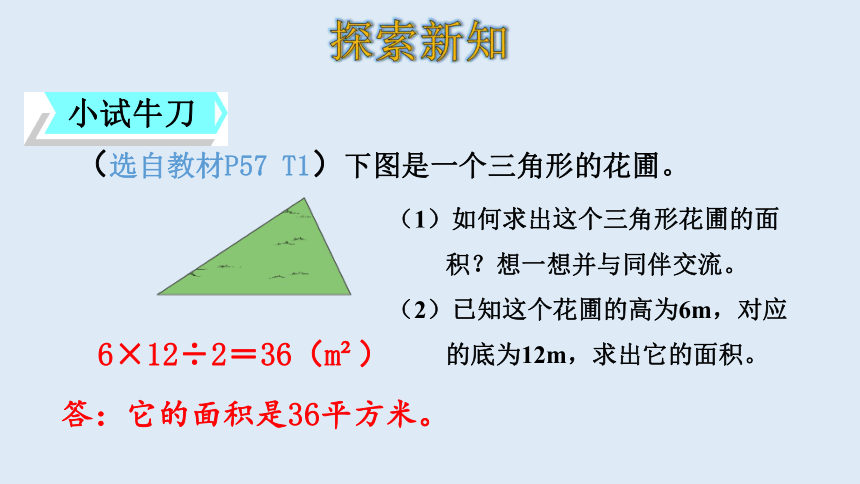
小试牛刀
(选自教材P57 T1)下图是一个三角形的花圃。
(1)如何求出这个三角形花圃的面积?想一想并与同伴交流。
(2)已知这个花圃的高为6m,对应的底为12m,求出它的面积。
6×12÷2=36(m?)
答:它的面积是36平方米。
例题分析
35.1×2÷9=7.8(dm)
一块三角形交通标志牌(如图),面积是35.1dm? ,底是9dm。这个底对应的高是多少分米?
答:这个底对应的高是7.8分米。
计算下列三角形的面积,你发现了什么?
S=ah÷2=3×5÷2=7.5(cm2)
同底等高的三角形的面积相等。
知识提炼
知识点:
等底等高的三角形的面积相等。
小试牛刀
(选自教材P58 T3)三角形彩旗的面积是570cm?,高是38cm,彩旗高对应的底是多少厘米?
570×2÷38=30(cm)
答:彩旗高对应的底是30厘米。
判断:两个面积相等的三角形一定能拼成一个平行四边形。 ( )
两个面积相等的三角形即便是底和高相等,只要形状不完全相同,就不能拼成一个平行四边形。
1.填空。
(1)三角形的面积=( ),用字母表示是( )。
(2)一个三角形与一个平行四边形等底等高,平行四边形的底
是3.6米,高是2.5米。三角形的面积是( )平方米, 平
行四边形的面积是( )平方米。
(3)一个三角形的面积是18平方分米,它的底是60厘米,它的高
是( )分米。
4.5
9
6
S=a×h÷2
底×高÷2
2.判断。(对的打“√”,错的打“×”)
(1)平行四边形的面积大于三角形的面积。 ( )
(2)底和高分别相等的两个三角形的面积相等。面积相
等的两个三角形的底和高也分别相等。 ( )
(3)三角形的面积等于平行四边形面积的一半。 ( )
(4)三角形的底越长,面积就越大。 ( )
(5)两个完全相同的直角三角形可以拼成一个长方形。( )
√
×
×
×
×
3.平行四边形ABCD的面积是42cm?,求三角形ADE的
面积是多少?
42÷2=21(cm?)
答:三角形ADE的面积是21平方厘米。
4.(选自教材P58 T4)在方格纸上再画两个不同的三角
形,使每个都与给出的三角形面积相等。
5.(选自教材P58 T5)图中哪个三角形的面积是左边平行四
边形面积的一半,哪个三角形的面积与左边平行四边形
的相等?想一想,并与同伴交流。
图①的面积是左边平行四边形面积的一半,图③的面积与左边平行四边形面积
等底等高的三角形的面积相等。
三角形的面积=底×高÷2( S=ah÷2 )。
作业1:完成教材P58练一练T7。
作业2:完成对应的练习题。
第 4 课时
探究活动:
三角形的面积
在实际情景中,认识计算三角形面积的必要性。
在自主探索中,经历推导三角形面积计算公式的过程,渗透转化思想。
能运用三角形的面积公式计算相关图形的面积,解决实际问题。(重点)
理解拼成的平行四边形和原来的三角形的关系。
(难点)
回顾前面所学知识,完成下列填空。
(1)把一个平行四边形,沿着高剪成两部分,平移
后可得到一个( )形,它的长相当于平行
四边形的( ),它的宽相当于平行四边形
的( )。
(2)平行四边形的底是 6 cm,高是 5 cm,面积是
( )cm?。
长方
底
高
30
例题分析
如何求出这面流动红旗的面积?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
数格子
请你把三角形转化成学过的图形。
底
高
底
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
长方形的面积=长×宽
三角形的面积=底×高÷2
长
宽
S=ah÷2
28cm
25cm
三角形的面积=底×高÷2
=28×25÷2
你能求出这面流动红旗的面积吗?
=350(cm?)
知识提炼
知识点:
三角形的面积=底×高÷2
S=ah÷2。
小试牛刀
(选自教材P57 T1)下图是一个三角形的花圃。
(1)如何求出这个三角形花圃的面积?想一想并与同伴交流。
(2)已知这个花圃的高为6m,对应的底为12m,求出它的面积。
6×12÷2=36(m?)
答:它的面积是36平方米。
例题分析
35.1×2÷9=7.8(dm)
一块三角形交通标志牌(如图),面积是35.1dm? ,底是9dm。这个底对应的高是多少分米?
答:这个底对应的高是7.8分米。
计算下列三角形的面积,你发现了什么?
S=ah÷2=3×5÷2=7.5(cm2)
同底等高的三角形的面积相等。
知识提炼
知识点:
等底等高的三角形的面积相等。
小试牛刀
(选自教材P58 T3)三角形彩旗的面积是570cm?,高是38cm,彩旗高对应的底是多少厘米?
570×2÷38=30(cm)
答:彩旗高对应的底是30厘米。
判断:两个面积相等的三角形一定能拼成一个平行四边形。 ( )
两个面积相等的三角形即便是底和高相等,只要形状不完全相同,就不能拼成一个平行四边形。
1.填空。
(1)三角形的面积=( ),用字母表示是( )。
(2)一个三角形与一个平行四边形等底等高,平行四边形的底
是3.6米,高是2.5米。三角形的面积是( )平方米, 平
行四边形的面积是( )平方米。
(3)一个三角形的面积是18平方分米,它的底是60厘米,它的高
是( )分米。
4.5
9
6
S=a×h÷2
底×高÷2
2.判断。(对的打“√”,错的打“×”)
(1)平行四边形的面积大于三角形的面积。 ( )
(2)底和高分别相等的两个三角形的面积相等。面积相
等的两个三角形的底和高也分别相等。 ( )
(3)三角形的面积等于平行四边形面积的一半。 ( )
(4)三角形的底越长,面积就越大。 ( )
(5)两个完全相同的直角三角形可以拼成一个长方形。( )
√
×
×
×
×
3.平行四边形ABCD的面积是42cm?,求三角形ADE的
面积是多少?
42÷2=21(cm?)
答:三角形ADE的面积是21平方厘米。
4.(选自教材P58 T4)在方格纸上再画两个不同的三角
形,使每个都与给出的三角形面积相等。
5.(选自教材P58 T5)图中哪个三角形的面积是左边平行四
边形面积的一半,哪个三角形的面积与左边平行四边形
的相等?想一想,并与同伴交流。
图①的面积是左边平行四边形面积的一半,图③的面积与左边平行四边形面积
等底等高的三角形的面积相等。
三角形的面积=底×高÷2( S=ah÷2 )。
作业1:完成教材P58练一练T7。
作业2:完成对应的练习题。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
