北师大版数学六年级上册1.7圆的面积(二) 课件(20张ppt)
文档属性
| 名称 | 北师大版数学六年级上册1.7圆的面积(二) 课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 19:44:21 | ||
图片预览







文档简介
第7课时 圆的面积(二)
第一单元 圆
1、结合具体情境,经历运用圆的面积公式解决实际问题的过
程,经历解决已知圆的周长求圆面积的实际问题的过程。
2、能灵活运用圆的周长公式、圆的面积公式解决生活中的简
单实际问题。
(重点)
3、感受数学与生活中的密切联系,培养数学应用意识。
(难点)
例题分析
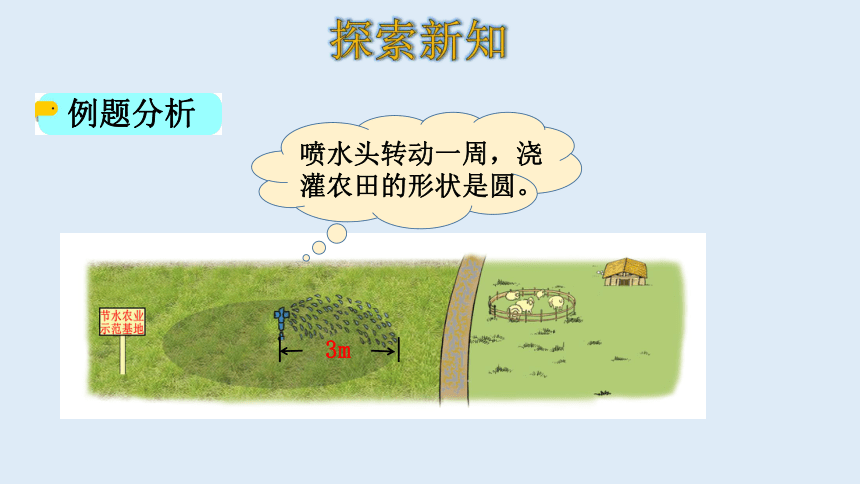
喷水头转动一周,浇灌农田的形状是圆。
3m
问:喷水半径是3 m,喷水头转动一周,能浇灌多
大面积的农田?
3.14×32
=3.14×9
=28.26(m?)
答:能浇灌28.26 m?的农田。
量得圆形羊圈的周长是125.6 m。这个羊圈的面积是多少平方米?
要计算圆形羊圈的面积,可以先求出羊圈的半径。
半径:125.6÷3.14÷2=20(m)
面积:3.14×202=1256(m?)
答:这个羊圈的面积是1256 m?。
求圆的面积必须知道圆的半径。当已知直径或周长,要求面积时,必须求出圆的半径,然后利用面积公式求出面积。
知识提炼
小明和小光每人有一根长6.28 m的铁丝,小明用它围成一个正方形,小光用它围成一个圆,问两人谁围成的图形的面积大。
小试牛刀
正方形的面积:(6.28÷4)2=2.4649(m?)
圆的面积:3.14×(6.28÷3.14÷2)2=3.14(m?)
3.14>2.4649
答:小光围成的图形的面积大。
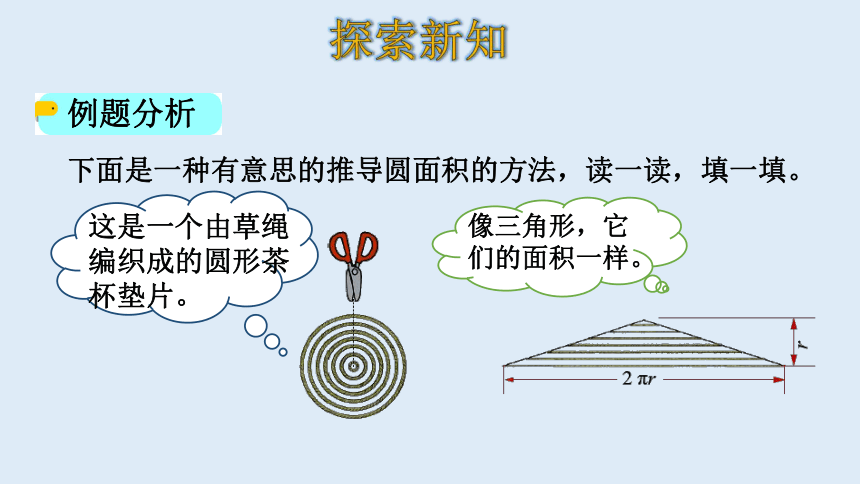
下面是一种有意思的推导圆面积的方法,读一读,填一填。
例题分析
这是一个由草绳编织成的圆形茶杯垫片。
像三角形,它们的面积一样。
仔细观察之后发现三角形的面积相当于圆的面积,三角形的底相当于圆的周长,高相当于圆的半径。
三角形的面积= ,所以圆的面积=
底×高
2
2πr×r
2
【同学们观察三角形,你发现了什么?】
知识提炼
圆的面积计算公式的推导方法有很多种,都是把圆转化成学过的图形来推导的。
求下各图形阴影部分的面积。
正方形面积:4×4=16(m?)
圆的面积:3.14×(4÷2)2=12.56(m?)
阴影部分面积:16-12.56=3.44(m?)
答:阴影部分的面积是3.44 m?。
小试牛刀
例 一个圆形纽扣的半径是1.5 cm,它的面积是多少?
错误解答:3.14×1.5?=3.14×3=9.42(cm?)
答:它的面积是9.42cm?。
错因分析:此题错在计算1.5?时,把1.5?当成1.5×2
计算了,而1.5?=1.5×1.5。
正确解答:3.14×1.5?=3.14×2.25=7.065(cm?)。
答:它的面积是7.065cm?。
1、一个圆形杯垫的半径是4cm,这个杯垫的面积是
多少平方厘米?
(选自教材P17练一练第1题)
3.14×42 =50.24(cm?)
答:这个杯垫的面积是50.24平方厘米。
2、有一个圆形蓄水池。它的周长约是31.4m,它的占地面
积约是多少?
半径:31.4÷3.14÷2=5(m)
面积:3.14×52=78.5(m2)
答:它的占地面积约是78.5平方厘米。
(选自教材P17练一练第2题)
3、有一个圆形蓄水池。它的周长约是31.4m,它的占地面
积约是多少?
(选自教材P17练一练第3题)
C
2
r
πr
r
πr2
4、北京天坛公园的回音壁是闻名世界的声学奇迹,它是
一道圆形围墙。圆的直径约为61.5米,周长与面积分
别是多少?(结果保留一位小数)
(选自教材P17练一练第4题)
周长:3.14×61.5≈193.1(m)
面积:3.14 ×(61.5÷2)2 ≈ 2969.1(m2)
答:它的周长约是193.1米,面积约是2969.1平方米。
5、一个运动场跑道的形状与大小如图。两边是半圆
形,中间是长方形,这个运动场的占地面积是多少?
(选自教材P17练一练第5题)
长方形面积:50×20=1000(m2)
半圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
答:这个运动场的占地面积是1314平方米。
1.求圆的面积必须知道圆的半径。当已知直径或周长,要
求面积时,必须求出圆的半径,然后利用面积公式求出
面积。
2.圆的面积计算公式的推导方法有很多种,都是把圆转化
成学过的图形来推导的。
作业1:完成教材P18练习一与本课相关的题目。
作业2:完成对应的练习题。
第一单元 圆
1、结合具体情境,经历运用圆的面积公式解决实际问题的过
程,经历解决已知圆的周长求圆面积的实际问题的过程。
2、能灵活运用圆的周长公式、圆的面积公式解决生活中的简
单实际问题。
(重点)
3、感受数学与生活中的密切联系,培养数学应用意识。
(难点)
例题分析
喷水头转动一周,浇灌农田的形状是圆。
3m
问:喷水半径是3 m,喷水头转动一周,能浇灌多
大面积的农田?
3.14×32
=3.14×9
=28.26(m?)
答:能浇灌28.26 m?的农田。
量得圆形羊圈的周长是125.6 m。这个羊圈的面积是多少平方米?
要计算圆形羊圈的面积,可以先求出羊圈的半径。
半径:125.6÷3.14÷2=20(m)
面积:3.14×202=1256(m?)
答:这个羊圈的面积是1256 m?。
求圆的面积必须知道圆的半径。当已知直径或周长,要求面积时,必须求出圆的半径,然后利用面积公式求出面积。
知识提炼
小明和小光每人有一根长6.28 m的铁丝,小明用它围成一个正方形,小光用它围成一个圆,问两人谁围成的图形的面积大。
小试牛刀
正方形的面积:(6.28÷4)2=2.4649(m?)
圆的面积:3.14×(6.28÷3.14÷2)2=3.14(m?)
3.14>2.4649
答:小光围成的图形的面积大。
下面是一种有意思的推导圆面积的方法,读一读,填一填。
例题分析
这是一个由草绳编织成的圆形茶杯垫片。
像三角形,它们的面积一样。
仔细观察之后发现三角形的面积相当于圆的面积,三角形的底相当于圆的周长,高相当于圆的半径。
三角形的面积= ,所以圆的面积=
底×高
2
2πr×r
2
【同学们观察三角形,你发现了什么?】
知识提炼
圆的面积计算公式的推导方法有很多种,都是把圆转化成学过的图形来推导的。
求下各图形阴影部分的面积。
正方形面积:4×4=16(m?)
圆的面积:3.14×(4÷2)2=12.56(m?)
阴影部分面积:16-12.56=3.44(m?)
答:阴影部分的面积是3.44 m?。
小试牛刀
例 一个圆形纽扣的半径是1.5 cm,它的面积是多少?
错误解答:3.14×1.5?=3.14×3=9.42(cm?)
答:它的面积是9.42cm?。
错因分析:此题错在计算1.5?时,把1.5?当成1.5×2
计算了,而1.5?=1.5×1.5。
正确解答:3.14×1.5?=3.14×2.25=7.065(cm?)。
答:它的面积是7.065cm?。
1、一个圆形杯垫的半径是4cm,这个杯垫的面积是
多少平方厘米?
(选自教材P17练一练第1题)
3.14×42 =50.24(cm?)
答:这个杯垫的面积是50.24平方厘米。
2、有一个圆形蓄水池。它的周长约是31.4m,它的占地面
积约是多少?
半径:31.4÷3.14÷2=5(m)
面积:3.14×52=78.5(m2)
答:它的占地面积约是78.5平方厘米。
(选自教材P17练一练第2题)
3、有一个圆形蓄水池。它的周长约是31.4m,它的占地面
积约是多少?
(选自教材P17练一练第3题)
C
2
r
πr
r
πr2
4、北京天坛公园的回音壁是闻名世界的声学奇迹,它是
一道圆形围墙。圆的直径约为61.5米,周长与面积分
别是多少?(结果保留一位小数)
(选自教材P17练一练第4题)
周长:3.14×61.5≈193.1(m)
面积:3.14 ×(61.5÷2)2 ≈ 2969.1(m2)
答:它的周长约是193.1米,面积约是2969.1平方米。
5、一个运动场跑道的形状与大小如图。两边是半圆
形,中间是长方形,这个运动场的占地面积是多少?
(选自教材P17练一练第5题)
长方形面积:50×20=1000(m2)
半圆面积:3.14×(20÷2)2=314(m2)
占地面积:1000+314=1314(m2)
答:这个运动场的占地面积是1314平方米。
1.求圆的面积必须知道圆的半径。当已知直径或周长,要
求面积时,必须求出圆的半径,然后利用面积公式求出
面积。
2.圆的面积计算公式的推导方法有很多种,都是把圆转化
成学过的图形来推导的。
作业1:完成教材P18练习一与本课相关的题目。
作业2:完成对应的练习题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
