北师大版数学六年级上册2.3 分数混合运算(三)课件(35张ppt)
文档属性
| 名称 | 北师大版数学六年级上册2.3 分数混合运算(三)课件(35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 00:00:00 | ||
图片预览











文档简介
分数混合运算(三)
第二单元 分数混合运算
第3课时
1.利用方程解决与分数运算有关的实际问题。
2.会表示题中的数量关系,培养分析、推理能力。
3.掌握“已知比一个数多(少)几分之几的数是
多少,求这个数”的解题方法。
(重点)
(难点)
一个数是36,另一个数比它多 ,求另一个数是多少?
1
3
36+(36× )=48
1
3
“一个数是36,比另一个数多 ,求另一个数”。这个问题和上面的问题有什么不同了?
1
3
①八月用水多少吨?说说你是如何思考的。
例题分析
九月比八月节约了 ,说明八月用水多。九月用水12吨,所以八月用水量一定大于12吨。
1
7
根据题意可知,八月的用水量是单位“1”,所以,我找到了两种方法来解决这个问题。
例题分析
方法一:九月比八月节约了 ,设八月用水量为x吨,九月比八月节约了 x吨,根据“八月的用水量-八月的用水量的 =九月的用水量”这一等量关系式列方程解答。
1
7
1
7
1
7
解:设八月用水x吨。
x=14
答:八月用水14吨。
x- x=12
1
7
x=12
6
7
方法二:九月比八月节约了 ,即九月占八月的1- = ,设八月用水量为x吨,根据“八月的用水量×(1- )=九月的用水量”这一等量关系式列方程解答。
1
7
6
7
1
7
1
7
x =14
x =12
6
7
解:设八月用水x吨。
答:八月用水14吨。
1
7
(1 - )x =12
例题分析
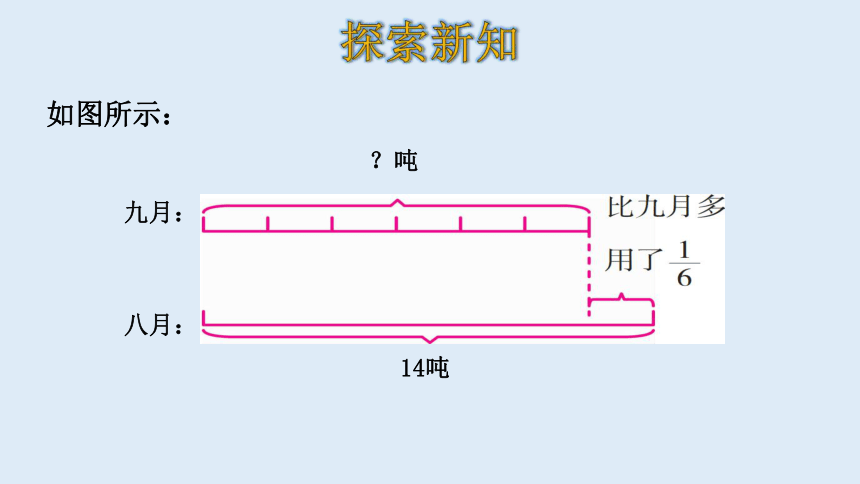
如果淘气家八月用水14吨,比九月多用了 ,九月用水多少吨?
1
6
比九月多用了 ,是把九月的水吨数看作单位“1”,可以画线段图如下:
1
6
九月:
八月:
如图所示:
?吨
14吨
方法一:八月比九月多用了 ,把九月的用水量看作单位“1”,八月比九月多的用水量可以表示为“九月的用水量× ”,所以求九月的用水量可根据数量关系“九月用水量+八月比九月多的用水量=八月用水量”列方程解答。
1
6
1
6
解:设九月用水x吨。
x=12
x+ x=14
1
6
x=14
7
6
答:九月用水12吨。
方法二:根据“八月比九月多用了 ”,把九月的用水量看作单位“1”,而八月比九月多用了 ,八月的用水量相当于九月(1+ ),根据分数乘法的意义,列方程解答。
1
6
1
6
1
6
(1+ )x=14
x=14
x=12
解:设九月用水x吨。
1
6
7
6
答:九月用水12吨。
知识提炼
“已知比一个数多(少)几分之几的数是多少,求这个数”的解题方法:
(1)先求出这个数占几分之几,再根据分数乘法的意义列出方程。
(2)先求出多(少)的几分之几是多少,再根据加减关系列出方程。
小试牛刀
有一池水,第一天放出水200吨,第二天放出的水比第一天少 ,第三天放出整池水的 ,全部放完,求这池水共有多少吨。
13
20
1
4
200×(1- )=150(吨)
1
4
200+150=350(吨)
350÷(1- )=1000(吨)
13
20
答:这池水共有1000吨。
书店运来一批文艺书,售出 后,还剩1360本。这批文艺书共多少本?
5
8
例题分析
我们可以根据题意画出线段图来加深对题目的理解,然后解答。
这个题目该怎么解答呢?
根据题意画出的线段图,如下所示:
通过这个线段图我想出两个方法来解答这个问题,让我来给大家分享一下吧!
方法一:把这批文艺书的总数看作单位“1”,“售出 ”,则售出的文艺书的本数可表示为“文艺书总数× ”,所以求“这批文艺书共有多少本”,可以根据数量关系“文艺书总数-售出文艺书本数=还剩的本数”列方程解答。
5
8
5
8
解:设这批文艺书共有x本。
x≈3627
答:这批文艺书共有3627本。
x- x=1360
5
8
x=1360
3
8
5
8
方法二:把这批文艺书的总数看作单位“1”,因为已经售出了 ,所以剩下的文艺书占总数的(1- ),剩下的文艺书可表示为“文艺书总数×(1- )”,所以求这批文艺书一共有多少本,可以根据数量关系“文艺书总数×(1- )=还剩的本数”列方程解答。
5
8
5
8
5
8
5
8
解:设这批文艺书共有x本。
x×(1- )=1360
x=1360
x≈3627
3
8
答:这批文艺书共有3627本。
“已知一部分量占总量的几分之几及另一部分量,求总量”的解题方法(列方程解):
(1)总量×(1-已知部分量占总量的分率)=另一部分量
(2)总量-总量×已知部分量占总量的分率=另一部分量
知识提炼
小试牛刀
1.填空。
(1)实验小学有男生480人,比女生多 ,实验小学有女生( )人。
(2)丽都酒店第四季度营业额为60万元,比计划多 ,丽都酒店第四季度计划营业额为( )万元。
5
7
1
3
280
45
例 水结成冰后,体积会比原来增加 。5 m?的冰融化成水,水的
体积是多少立方米?
1
10
错误解答:
1
10
5+5×
= 5 +
1
2
= 5
1
2
(立方米)
答:水的体积是5 立方米。
1
2
错因分析:此题错在没有找准单位“1”的量,对于分率 而言,是把水的体积看作单位“1”。那么水的体积是未知量,用方程法解答比较简便。
解:设水的体积是x m?。
(1+ )x=5
x=4
6
11
1
10
正确解答:
答:水的体积是 4 立方米。
6
11
1
10
1、
B
2、
B
2、
5÷(1- )=20(kg)
3
4
答:这袋米重20kg。
3.水结成冰后,体积增加 。一块体积是143dm3的冰化成水后,体积是多少立方分米?
1
10
解:设冰化成水后体积是x立方分米。
(1+ )x=143
1
10
x=130
答:冰化成水后体积是130立方分米。
1.光明小学六年级有95人,比五年级的人数少 ,五年
级有多少人?
1
6
⑴找到题中的等量关系,画一画,说一说。
⑵列出方程进行解答。
解:设五年级有x人。
(1- )x=95
1
6
5
6
x=95
x=114
答:五年级有114人。
2.看图列式计算。
解:设一件上衣售价 x 元。
x - x = 120
2
5
x = 200
3.解方程。
3.解方程。
解: x =102-4
7
10
x =98
7
10
x =140
1
4
x- x =
3
8
解: x =
3
4
3
8
x =
1
2
4+ x =102
7
10
x-0.8 x =22
解:0.2 x =22
x =110
解: x =42
7
6
x =36
2
3
x+ x =42
1
2
解:x =
x+ =6
3
4
x- x =
1
4
1
2
解:x =
3
4
21
4
(2)总量-总量×已知部分量占总量的分率=另一部分量
“已知比一个数多(少)几分之几的数是多少,求这个数”的解题方法:
(1)先求出这个数占几分之几,再根据分数乘法的
意义列出方程。
(2)先求出多(少)的几分之几是多少,再根据加
减关系列出方程。
(2)总量-总量×已知部分量占总量的分率=另一部分量
“已知一部分量占总量的几分之几及另一部分量,求总量”的解题方法(列方程解):
(1)总量×(1-已知部分量占总量的分率)
=另一部分量
(2)总量-总量×已知部分量占总量的分率
=另一部分量
作业1:完成教材P28~P29练一练。
作业2:完成对应的练习题。
第二单元 分数混合运算
第3课时
1.利用方程解决与分数运算有关的实际问题。
2.会表示题中的数量关系,培养分析、推理能力。
3.掌握“已知比一个数多(少)几分之几的数是
多少,求这个数”的解题方法。
(重点)
(难点)
一个数是36,另一个数比它多 ,求另一个数是多少?
1
3
36+(36× )=48
1
3
“一个数是36,比另一个数多 ,求另一个数”。这个问题和上面的问题有什么不同了?
1
3
①八月用水多少吨?说说你是如何思考的。
例题分析
九月比八月节约了 ,说明八月用水多。九月用水12吨,所以八月用水量一定大于12吨。
1
7
根据题意可知,八月的用水量是单位“1”,所以,我找到了两种方法来解决这个问题。
例题分析
方法一:九月比八月节约了 ,设八月用水量为x吨,九月比八月节约了 x吨,根据“八月的用水量-八月的用水量的 =九月的用水量”这一等量关系式列方程解答。
1
7
1
7
1
7
解:设八月用水x吨。
x=14
答:八月用水14吨。
x- x=12
1
7
x=12
6
7
方法二:九月比八月节约了 ,即九月占八月的1- = ,设八月用水量为x吨,根据“八月的用水量×(1- )=九月的用水量”这一等量关系式列方程解答。
1
7
6
7
1
7
1
7
x =14
x =12
6
7
解:设八月用水x吨。
答:八月用水14吨。
1
7
(1 - )x =12
例题分析
如果淘气家八月用水14吨,比九月多用了 ,九月用水多少吨?
1
6
比九月多用了 ,是把九月的水吨数看作单位“1”,可以画线段图如下:
1
6
九月:
八月:
如图所示:
?吨
14吨
方法一:八月比九月多用了 ,把九月的用水量看作单位“1”,八月比九月多的用水量可以表示为“九月的用水量× ”,所以求九月的用水量可根据数量关系“九月用水量+八月比九月多的用水量=八月用水量”列方程解答。
1
6
1
6
解:设九月用水x吨。
x=12
x+ x=14
1
6
x=14
7
6
答:九月用水12吨。
方法二:根据“八月比九月多用了 ”,把九月的用水量看作单位“1”,而八月比九月多用了 ,八月的用水量相当于九月(1+ ),根据分数乘法的意义,列方程解答。
1
6
1
6
1
6
(1+ )x=14
x=14
x=12
解:设九月用水x吨。
1
6
7
6
答:九月用水12吨。
知识提炼
“已知比一个数多(少)几分之几的数是多少,求这个数”的解题方法:
(1)先求出这个数占几分之几,再根据分数乘法的意义列出方程。
(2)先求出多(少)的几分之几是多少,再根据加减关系列出方程。
小试牛刀
有一池水,第一天放出水200吨,第二天放出的水比第一天少 ,第三天放出整池水的 ,全部放完,求这池水共有多少吨。
13
20
1
4
200×(1- )=150(吨)
1
4
200+150=350(吨)
350÷(1- )=1000(吨)
13
20
答:这池水共有1000吨。
书店运来一批文艺书,售出 后,还剩1360本。这批文艺书共多少本?
5
8
例题分析
我们可以根据题意画出线段图来加深对题目的理解,然后解答。
这个题目该怎么解答呢?
根据题意画出的线段图,如下所示:
通过这个线段图我想出两个方法来解答这个问题,让我来给大家分享一下吧!
方法一:把这批文艺书的总数看作单位“1”,“售出 ”,则售出的文艺书的本数可表示为“文艺书总数× ”,所以求“这批文艺书共有多少本”,可以根据数量关系“文艺书总数-售出文艺书本数=还剩的本数”列方程解答。
5
8
5
8
解:设这批文艺书共有x本。
x≈3627
答:这批文艺书共有3627本。
x- x=1360
5
8
x=1360
3
8
5
8
方法二:把这批文艺书的总数看作单位“1”,因为已经售出了 ,所以剩下的文艺书占总数的(1- ),剩下的文艺书可表示为“文艺书总数×(1- )”,所以求这批文艺书一共有多少本,可以根据数量关系“文艺书总数×(1- )=还剩的本数”列方程解答。
5
8
5
8
5
8
5
8
解:设这批文艺书共有x本。
x×(1- )=1360
x=1360
x≈3627
3
8
答:这批文艺书共有3627本。
“已知一部分量占总量的几分之几及另一部分量,求总量”的解题方法(列方程解):
(1)总量×(1-已知部分量占总量的分率)=另一部分量
(2)总量-总量×已知部分量占总量的分率=另一部分量
知识提炼
小试牛刀
1.填空。
(1)实验小学有男生480人,比女生多 ,实验小学有女生( )人。
(2)丽都酒店第四季度营业额为60万元,比计划多 ,丽都酒店第四季度计划营业额为( )万元。
5
7
1
3
280
45
例 水结成冰后,体积会比原来增加 。5 m?的冰融化成水,水的
体积是多少立方米?
1
10
错误解答:
1
10
5+5×
= 5 +
1
2
= 5
1
2
(立方米)
答:水的体积是5 立方米。
1
2
错因分析:此题错在没有找准单位“1”的量,对于分率 而言,是把水的体积看作单位“1”。那么水的体积是未知量,用方程法解答比较简便。
解:设水的体积是x m?。
(1+ )x=5
x=4
6
11
1
10
正确解答:
答:水的体积是 4 立方米。
6
11
1
10
1、
B
2、
B
2、
5÷(1- )=20(kg)
3
4
答:这袋米重20kg。
3.水结成冰后,体积增加 。一块体积是143dm3的冰化成水后,体积是多少立方分米?
1
10
解:设冰化成水后体积是x立方分米。
(1+ )x=143
1
10
x=130
答:冰化成水后体积是130立方分米。
1.光明小学六年级有95人,比五年级的人数少 ,五年
级有多少人?
1
6
⑴找到题中的等量关系,画一画,说一说。
⑵列出方程进行解答。
解:设五年级有x人。
(1- )x=95
1
6
5
6
x=95
x=114
答:五年级有114人。
2.看图列式计算。
解:设一件上衣售价 x 元。
x - x = 120
2
5
x = 200
3.解方程。
3.解方程。
解: x =102-4
7
10
x =98
7
10
x =140
1
4
x- x =
3
8
解: x =
3
4
3
8
x =
1
2
4+ x =102
7
10
x-0.8 x =22
解:0.2 x =22
x =110
解: x =42
7
6
x =36
2
3
x+ x =42
1
2
解:x =
x+ =6
3
4
x- x =
1
4
1
2
解:x =
3
4
21
4
(2)总量-总量×已知部分量占总量的分率=另一部分量
“已知比一个数多(少)几分之几的数是多少,求这个数”的解题方法:
(1)先求出这个数占几分之几,再根据分数乘法的
意义列出方程。
(2)先求出多(少)的几分之几是多少,再根据加
减关系列出方程。
(2)总量-总量×已知部分量占总量的分率=另一部分量
“已知一部分量占总量的几分之几及另一部分量,求总量”的解题方法(列方程解):
(1)总量×(1-已知部分量占总量的分率)
=另一部分量
(2)总量-总量×已知部分量占总量的分率
=另一部分量
作业1:完成教材P28~P29练一练。
作业2:完成对应的练习题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
