北师大版数学六年级上册6.1 生活中的比 课件(39张ppt)
文档属性
| 名称 | 北师大版数学六年级上册6.1 生活中的比 课件(39张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 20:14:23 | ||
图片预览








文档简介
第六单元 比的认识
第1课时 生活中的比
1.经历从具体情境中抽象出比的过程,理解比的意义。
2.能正确读写比,会求比值,理解比与除法、分数的
关系。
3.能利用比的知识解决一些简单的生活问题。
(重点)
(难点)
A
C
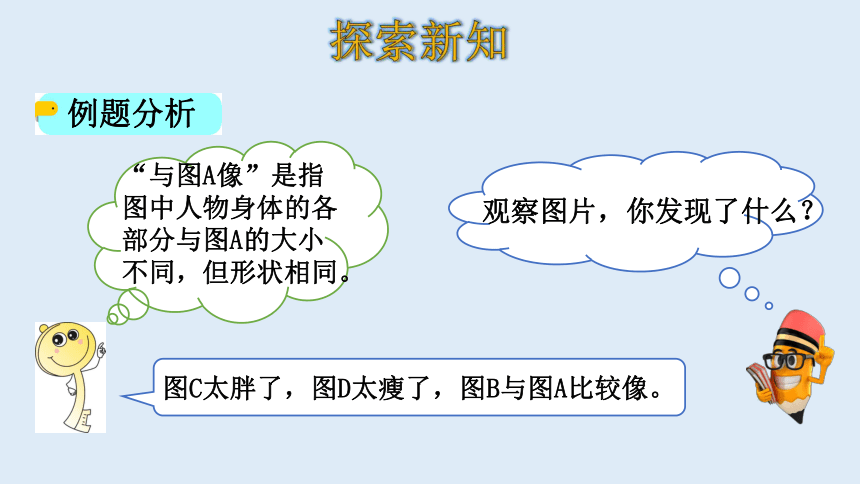
观察右面的图片,哪几张图片与A像?右面这些图片的长和宽有什么关系?
真有趣!
B
D
E
例题分析
“与图A像”是指图中人物身体的各部分与图A的大小不同,但形状相同。
观察图片,你发现了什么?
图C太胖了,图D太瘦了,图B与图A比较像。
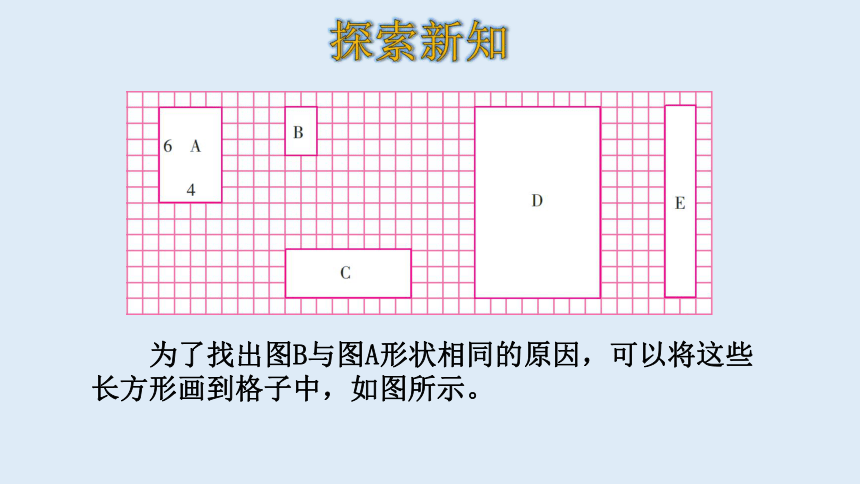
为了找出图B与图A形状相同的原因,可以将这些长方形画到格子中,如图所示。
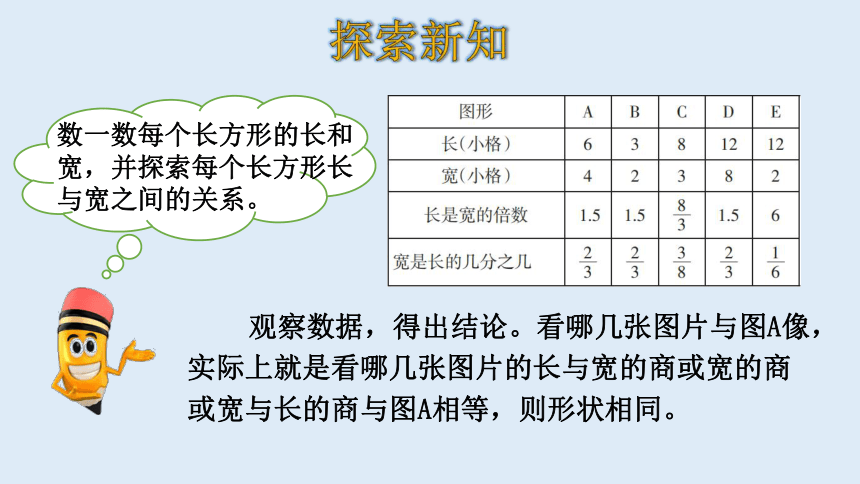
数一数每个长方形的长和宽,并探索每个长方形长与宽之间的关系。
观察数据,得出结论。看哪几张图片与图A像,实际上就是看哪几张图片的长与宽的商或宽的商或宽与长的商与图A相等,则形状相同。
知识提炼
通过分析比较“图片像不像”可知:生活中两个数量之间存在“倍比”关系。
(1)体育比赛中的比分可以记作2∶0,所以比的后项可以是0。
( )
小试牛刀
(2) 既可以看成一个分数,又可以看成一个比,还可以看成
一个比值。( )
1
6
(3)最小的质数与它的倒数的比的比值是1。( )
判断对错
×
×
√
两个数相除,又叫作这两个数的比。例如:一个长方形的长是6,宽是4,长和宽的比是6比4,宽和长的比是4比6。
比的含义
什么叫比?怎么读、写比?
比的读、写方法及各部分名称。
(1)写法:6比4写作6∶4,其中“∶”
是比号。
(2)读法:“∶”读作“比”。如6∶4读
作6比4。
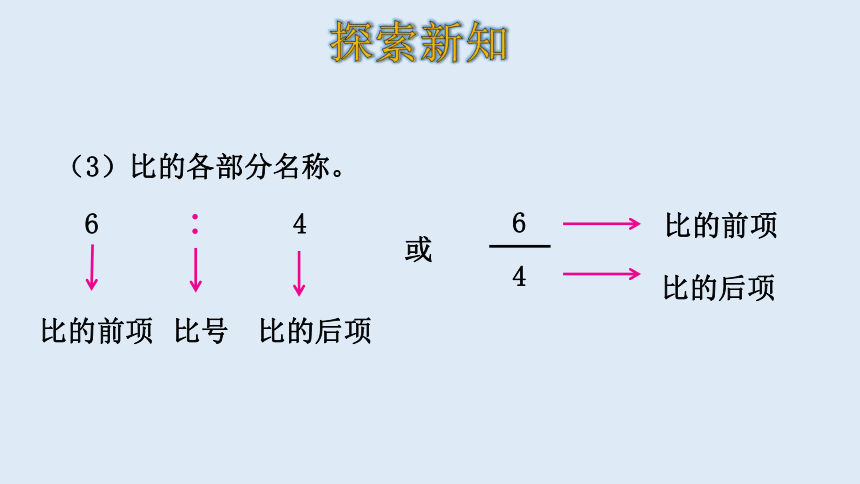
(3)比的各部分名称。
6 : 4
比的前项
比号
比的后项
或
6
4
比的前项
比的后项
求比值的方法:用比的前项除以比的后项所得的商就是这
个比的比值。比值可以是分数,也可以是
小数或整数。例如:6∶4=6÷4= =
1.5,6是这个比的前项,4是这个比的后项,
1.5是6∶4的比值。
6
4
1.两个数相除,又叫作这两个数的比。
2.“∶”是比号,读作“比”,比号前面的数
是比的前项,比号后面的数是比的后项。
3.用比的前项除以比的后项得到一个数,这个
数就是比值。
知识提炼
小试牛刀
根据下列信息写出比。
路程与时间的比是 。
付的钱数与买的米数的比是 。
120∶2
72∶4
(选自教材P71练一练第3题)
说说两边图中语句中的含义。
左图:甘蔗汁和水的体积比是1比2,表示水是甘蔗汁含量的2倍,1份甘蔗汁2份水,2份甘蔗汁4份水。
右图:树高和影长的比是6比3,表示树高是影长的2倍,影长是树高的 。
1
2
同学们明白了它们的含义了么?相信你们是最棒的!
填一填。
例题分析
谁的速度更快?
比较谁的速度快,实际上就是比较路程与时间的比的比值(即速度)的大小。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
路程
时间
路程与
时间的比
速度
马拉松选手
40km
2时
骑车人
45km
3时
填一填。
40:2
20千米/时
45:3
15千米/时
40∶2=40÷2=20
求比值:
45∶3=45÷3=15
正确解答:
因为20>15,所以马拉松选手的速度快。
填一填
(1)哪种苹果最便宜?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}品种
总价
数量
总价与
数量的比
单价
A
9元
2kg
B
15元
3kg
C
12元
3kg
已知A、B、C三种苹果的总价和数量,比较哪种苹果最便宜,实际上就是比较总价与数量的比的比值(即单价)的大小。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}品种
总价
数量
总价与
数量的比
单价
A
9元
2kg
B
15元
3kg
C
12元
3kg
9:2
15:3
4.5元
5元
12:3
4元
填一填:
9∶2=9÷2=4.5
15∶3=15÷3=5
12∶3=12÷3=4
求比值:
正确解答:
因为4<4.5<5,所以C种苹果最便宜。
1.两个同类量进行比较时,比表示两个数量之
间的倍比关系。
2.两个相关联的非同类量进行比较时,它们的
比表示一个新的量。
知识提炼
小试牛刀
根据下列信息写出比。
女生人数与全班人数的比是 。
(2)
正方形周长与边长的比是 。
正方形面积与边长的比是 。
11∶20
4∶1
3∶1
(1)
(选自教材P71练一练第4题)
比与分数、除法之间的联系。
比的前项相当于被除数,比的后项相当于除数,比值相当于商,比号相当于除号。
想一想,比与分数,除法有什么关系?
比与除法相比:
比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线。
比与分数相比:
知识提炼
1.比表示两个数之间的关系;分数是一种
数;除法是一种运算。
2.列表格表示比与分数、除法之间的关系。
小试牛刀
填一填。
(1)两个数相除,又叫作这两个数的( )。在A:B=C
中,A是这个比的( ),B是这个比的( ),
C是( )。
(2)中国国家乒乓球队队服上的一面是五星红旗,旗长6 cm,
宽4 cm。长和宽的比是( ):( ),比值是
( )。长与周长的比是( ):( ),比值
是( )。
比
前项
后项
比值
6
4
3
2
6
20
3
10
例 填空:小明看一本漫画书用1小时,小东看同一本
漫画书用43分钟,小明和小东所用时间的比是( )。
错误解答:1∶43
错因分析:虽然本题中1小时与43分钟属于同类量,但是单
位不统一,应先统一单位。
正确解答:60∶43
1.全国野生大熊猫数量最多的三个县均在四川,分别是平武县
230只,汶川县187只,宝兴县143只。平武县与汶川县拥有
野生大熊猫数量的比是多少?
230∶187
答:平县与汶川县拥有野生大熊猫数量的比
是230∶187。
2.小兰的身高是1 m,爸爸的身高是170 cm。能不能说爸
爸和小兰身高的比是170:1?为什么?
答:不能。单位不统一,不能直接比,应该
化成相同单位再比。
3.两个长方形重叠部分的面积相当于大长方形面积的 ,相
当于小长方形面积的 。
1
8
1
6
(1)把重叠部分的面积看作1,那么小长方形的面积为
( ),大长方形的面积为( )。
(2)大长方形和小长方形的面积比是
( )。
6
8
8∶6
4.看图回答问题。
(1)你发现这些图形的长、宽
有什么关系?
答:我发现最大的图形
和最小的图形的长
和宽的比都是4∶1。
(答案不唯一)
(2)写出几个比。
答:如:8∶5,8∶3,4∶3等。
(答案不唯一)
5.你能说一个用3∶4表示的情境吗?
在一次学校组织的体检中,我发现了小红和小明的身高是3∶4。
(答案不唯一)
1.通过分析比较“图片像不像”可知:生活中两个数
量之间存在“倍比”关系。
2.两个数相除,又叫作这两个数的比。
3.“∶”是比号,读作“比”,比号前面的数是比的
前项,比号后面的数是比的后项。
5.两个同类量进行比较时,比表示两个数量之间的
倍比关系。
6.两个相关联的非同类量进行比较时,它们的比表
示一个新的量。
4.用比的前项除以比的后项得到一个数,这个数
就是比值。
7.比表示两个数之间的关系;分数是一种数;除
法是一种运算。
8.列表格表示比与分数、除法之间的关系。
作业1:完成教材P71练一练5、6题。
作业2:完成对应的练习题。
第1课时 生活中的比
1.经历从具体情境中抽象出比的过程,理解比的意义。
2.能正确读写比,会求比值,理解比与除法、分数的
关系。
3.能利用比的知识解决一些简单的生活问题。
(重点)
(难点)
A
C
观察右面的图片,哪几张图片与A像?右面这些图片的长和宽有什么关系?
真有趣!
B
D
E
例题分析
“与图A像”是指图中人物身体的各部分与图A的大小不同,但形状相同。
观察图片,你发现了什么?
图C太胖了,图D太瘦了,图B与图A比较像。
为了找出图B与图A形状相同的原因,可以将这些长方形画到格子中,如图所示。
数一数每个长方形的长和宽,并探索每个长方形长与宽之间的关系。
观察数据,得出结论。看哪几张图片与图A像,实际上就是看哪几张图片的长与宽的商或宽的商或宽与长的商与图A相等,则形状相同。
知识提炼
通过分析比较“图片像不像”可知:生活中两个数量之间存在“倍比”关系。
(1)体育比赛中的比分可以记作2∶0,所以比的后项可以是0。
( )
小试牛刀
(2) 既可以看成一个分数,又可以看成一个比,还可以看成
一个比值。( )
1
6
(3)最小的质数与它的倒数的比的比值是1。( )
判断对错
×
×
√
两个数相除,又叫作这两个数的比。例如:一个长方形的长是6,宽是4,长和宽的比是6比4,宽和长的比是4比6。
比的含义
什么叫比?怎么读、写比?
比的读、写方法及各部分名称。
(1)写法:6比4写作6∶4,其中“∶”
是比号。
(2)读法:“∶”读作“比”。如6∶4读
作6比4。
(3)比的各部分名称。
6 : 4
比的前项
比号
比的后项
或
6
4
比的前项
比的后项
求比值的方法:用比的前项除以比的后项所得的商就是这
个比的比值。比值可以是分数,也可以是
小数或整数。例如:6∶4=6÷4= =
1.5,6是这个比的前项,4是这个比的后项,
1.5是6∶4的比值。
6
4
1.两个数相除,又叫作这两个数的比。
2.“∶”是比号,读作“比”,比号前面的数
是比的前项,比号后面的数是比的后项。
3.用比的前项除以比的后项得到一个数,这个
数就是比值。
知识提炼
小试牛刀
根据下列信息写出比。
路程与时间的比是 。
付的钱数与买的米数的比是 。
120∶2
72∶4
(选自教材P71练一练第3题)
说说两边图中语句中的含义。
左图:甘蔗汁和水的体积比是1比2,表示水是甘蔗汁含量的2倍,1份甘蔗汁2份水,2份甘蔗汁4份水。
右图:树高和影长的比是6比3,表示树高是影长的2倍,影长是树高的 。
1
2
同学们明白了它们的含义了么?相信你们是最棒的!
填一填。
例题分析
谁的速度更快?
比较谁的速度快,实际上就是比较路程与时间的比的比值(即速度)的大小。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
路程
时间
路程与
时间的比
速度
马拉松选手
40km
2时
骑车人
45km
3时
填一填。
40:2
20千米/时
45:3
15千米/时
40∶2=40÷2=20
求比值:
45∶3=45÷3=15
正确解答:
因为20>15,所以马拉松选手的速度快。
填一填
(1)哪种苹果最便宜?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}品种
总价
数量
总价与
数量的比
单价
A
9元
2kg
B
15元
3kg
C
12元
3kg
已知A、B、C三种苹果的总价和数量,比较哪种苹果最便宜,实际上就是比较总价与数量的比的比值(即单价)的大小。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}品种
总价
数量
总价与
数量的比
单价
A
9元
2kg
B
15元
3kg
C
12元
3kg
9:2
15:3
4.5元
5元
12:3
4元
填一填:
9∶2=9÷2=4.5
15∶3=15÷3=5
12∶3=12÷3=4
求比值:
正确解答:
因为4<4.5<5,所以C种苹果最便宜。
1.两个同类量进行比较时,比表示两个数量之
间的倍比关系。
2.两个相关联的非同类量进行比较时,它们的
比表示一个新的量。
知识提炼
小试牛刀
根据下列信息写出比。
女生人数与全班人数的比是 。
(2)
正方形周长与边长的比是 。
正方形面积与边长的比是 。
11∶20
4∶1
3∶1
(1)
(选自教材P71练一练第4题)
比与分数、除法之间的联系。
比的前项相当于被除数,比的后项相当于除数,比值相当于商,比号相当于除号。
想一想,比与分数,除法有什么关系?
比与除法相比:
比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线。
比与分数相比:
知识提炼
1.比表示两个数之间的关系;分数是一种
数;除法是一种运算。
2.列表格表示比与分数、除法之间的关系。
小试牛刀
填一填。
(1)两个数相除,又叫作这两个数的( )。在A:B=C
中,A是这个比的( ),B是这个比的( ),
C是( )。
(2)中国国家乒乓球队队服上的一面是五星红旗,旗长6 cm,
宽4 cm。长和宽的比是( ):( ),比值是
( )。长与周长的比是( ):( ),比值
是( )。
比
前项
后项
比值
6
4
3
2
6
20
3
10
例 填空:小明看一本漫画书用1小时,小东看同一本
漫画书用43分钟,小明和小东所用时间的比是( )。
错误解答:1∶43
错因分析:虽然本题中1小时与43分钟属于同类量,但是单
位不统一,应先统一单位。
正确解答:60∶43
1.全国野生大熊猫数量最多的三个县均在四川,分别是平武县
230只,汶川县187只,宝兴县143只。平武县与汶川县拥有
野生大熊猫数量的比是多少?
230∶187
答:平县与汶川县拥有野生大熊猫数量的比
是230∶187。
2.小兰的身高是1 m,爸爸的身高是170 cm。能不能说爸
爸和小兰身高的比是170:1?为什么?
答:不能。单位不统一,不能直接比,应该
化成相同单位再比。
3.两个长方形重叠部分的面积相当于大长方形面积的 ,相
当于小长方形面积的 。
1
8
1
6
(1)把重叠部分的面积看作1,那么小长方形的面积为
( ),大长方形的面积为( )。
(2)大长方形和小长方形的面积比是
( )。
6
8
8∶6
4.看图回答问题。
(1)你发现这些图形的长、宽
有什么关系?
答:我发现最大的图形
和最小的图形的长
和宽的比都是4∶1。
(答案不唯一)
(2)写出几个比。
答:如:8∶5,8∶3,4∶3等。
(答案不唯一)
5.你能说一个用3∶4表示的情境吗?
在一次学校组织的体检中,我发现了小红和小明的身高是3∶4。
(答案不唯一)
1.通过分析比较“图片像不像”可知:生活中两个数
量之间存在“倍比”关系。
2.两个数相除,又叫作这两个数的比。
3.“∶”是比号,读作“比”,比号前面的数是比的
前项,比号后面的数是比的后项。
5.两个同类量进行比较时,比表示两个数量之间的
倍比关系。
6.两个相关联的非同类量进行比较时,它们的比表
示一个新的量。
4.用比的前项除以比的后项得到一个数,这个数
就是比值。
7.比表示两个数之间的关系;分数是一种数;除
法是一种运算。
8.列表格表示比与分数、除法之间的关系。
作业1:完成教材P71练一练5、6题。
作业2:完成对应的练习题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
