华东师大版七年级数学上册第五章相交线与平行线单元测试题(含答案)
文档属性
| 名称 | 华东师大版七年级数学上册第五章相交线与平行线单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 168.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-13 21:19:23 | ||
图片预览

文档简介
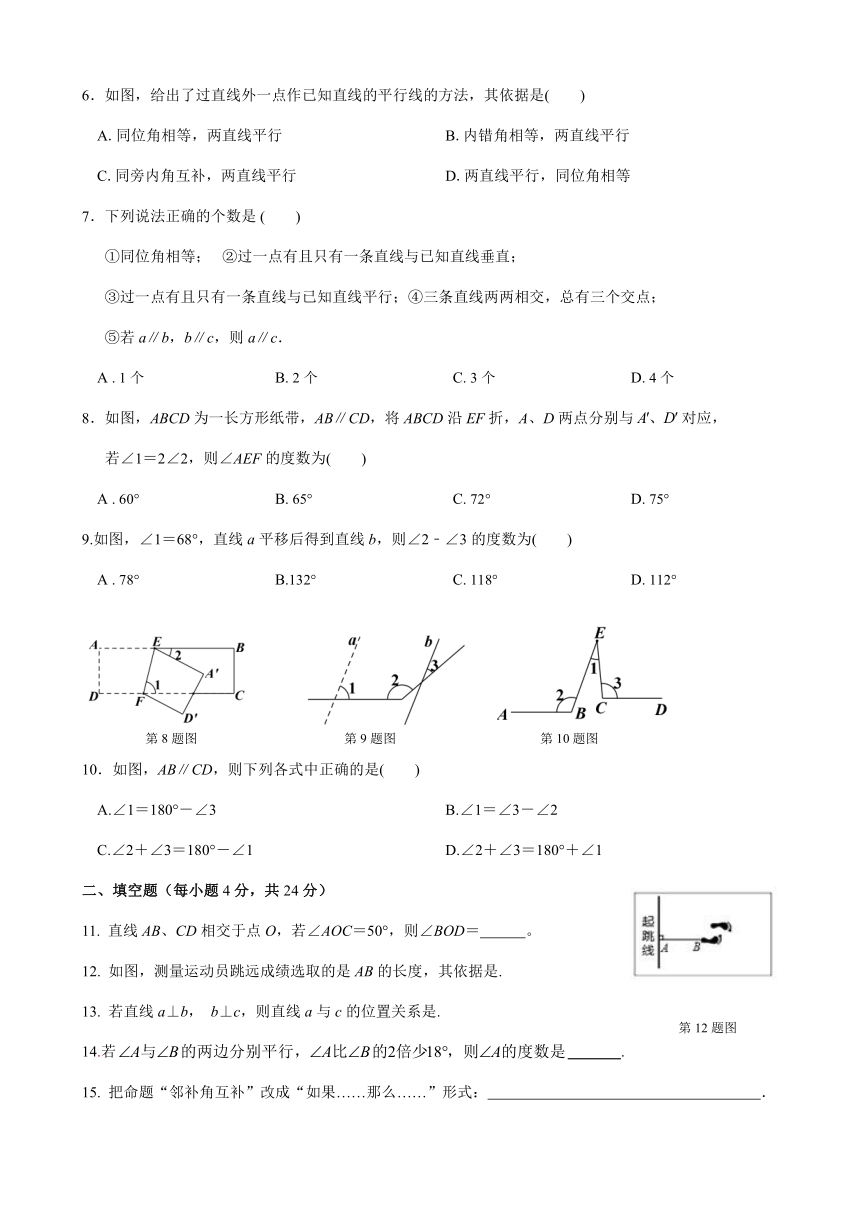
华东师大版七年级数学上册第五章相交线与平行线单元测试题
一、选择题(每小题4分,共40分)
1.下列图形可以由一个图形经过平移变换得到的是(
)
A
.
B.
C.
D.
2.在下列图形中,由∠1=∠2
能得到
AB∥CD
的是(
)
A
.
B.
C.
D.
3.对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A
.
a=3,b=2
B.
a=﹣3,b=2
C.
a=3,b=﹣1
D.
a=﹣1,b=3
4.如图,下列判断中错误的是(
)
A
.∠A与∠1是同位角
B.∠A与∠B是同旁内角
C.∠4与∠1是内错角
D.∠1与∠3是同位角
5.如图,∠BAC=90°,AD⊥BC于点D,则下列结论中错误的是(
)
A.点C到AB的垂线段是线段AC
B.点A到BC的距离是线段AD的长度
C.线段AB的长度是点B到AC的距离
D.线段AB是点B到AC的距离
(
第
4
题图
)
(
第
6
题图
)
(
第
5
题图
)
6.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
7.下列说法正确的个数是?( )
①同位角相等;?
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A
.
1个
B.
2个
C.
3个
D.
4个
8.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A、D两点分别与对应,
若∠1=2∠2,则∠AEF的度数为( )
A
.
60°
B.
65°
C.
72°
D.
75°
9.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )
A
.
78°
B.132°
C.
118°
D.
112°
(
第
9
题图
)
(
第
10
题图
)
(
第
8
题图
)
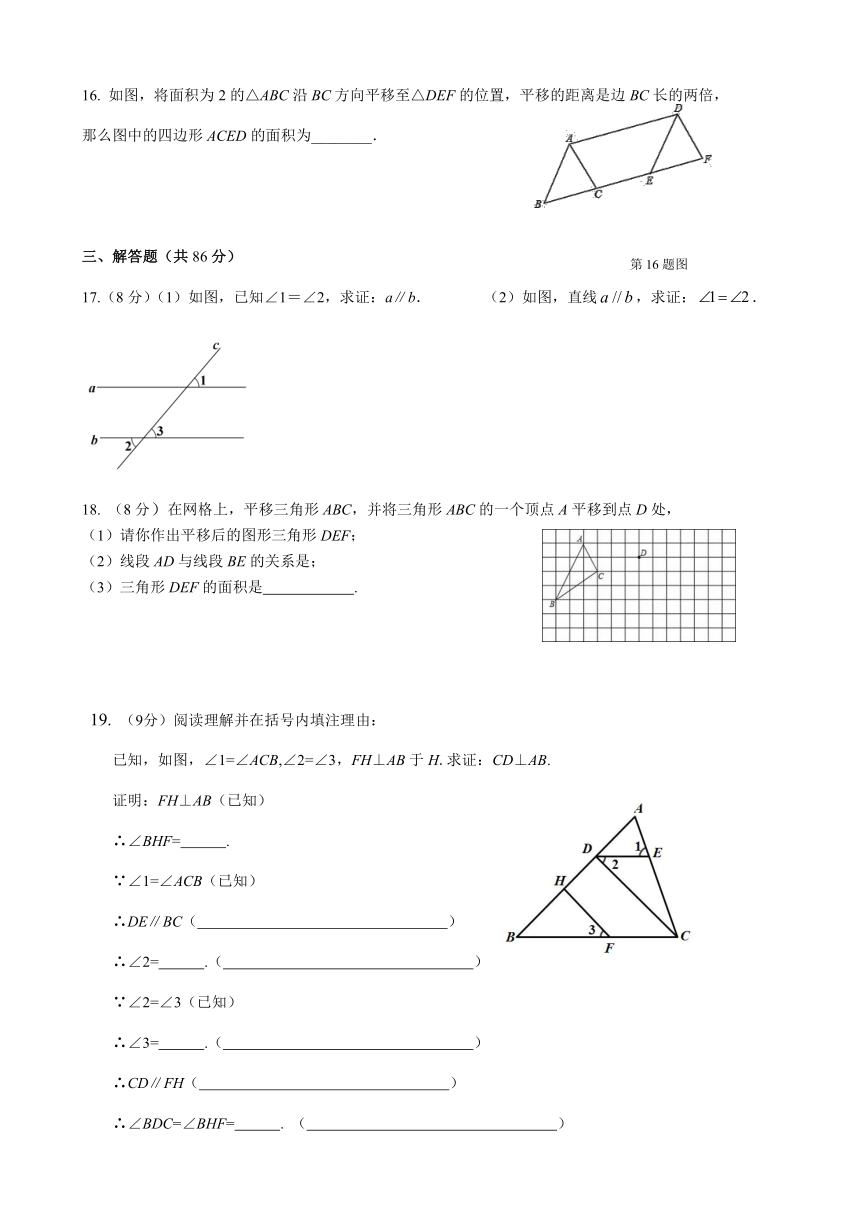
10.如图,AB∥CD,则下列各式中正确的是( )
A.∠1=180°-∠3
B.∠1=∠3-∠2
C.∠2+∠3=180°-∠1
D.∠2+∠3=180°+∠1
二、填空题(每小题4分,共24分)
11.
直线AB、CD相交于点O,若∠AOC=50°,则∠BOD= ??
。
12.
如图,测量运动员跳远成绩选取的是AB的长度,其依据是.
(
第
12
题图
)13.
若直线a⊥b,
b⊥c,则直线a与c的位置关系是.
14.若
.
15.
把命题“邻补角互补”改成“如果……那么……”形式:
.
16.
如图,将面积为2的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,
那么图中的四边形ACED的面积为________.
(
第
16
题图
)三、解答题(共86分)
17.(8分)(1)如图,已知∠1=∠2,求证:a∥b.
(2)如图,直线,求证:.
(8分)在网格上,平移三角形ABC,并将三角形ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形三角形DEF;
(2)线段AD与线段BE的关系是;
(3)三角形DEF的面积是
.
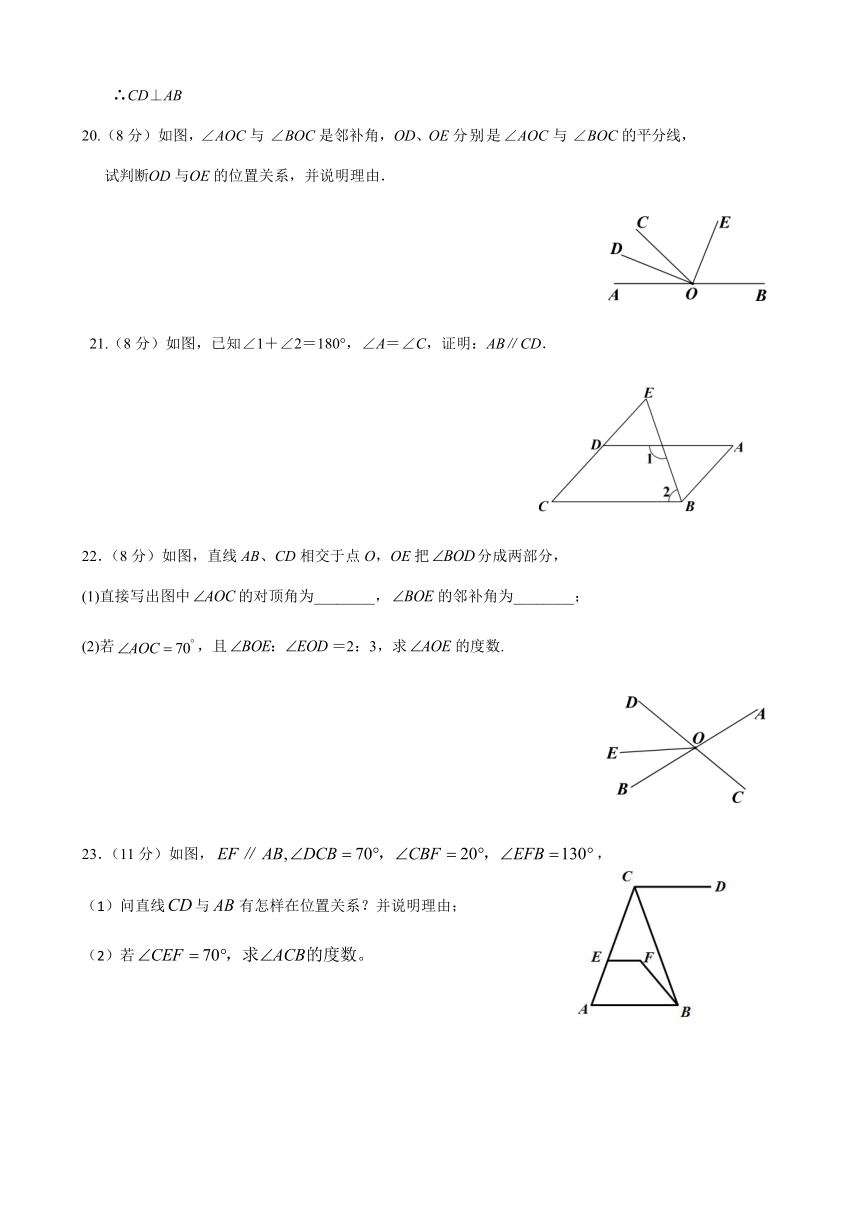
19.
(9分)阅读理解并在括号内填注理由:
已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.求证:CD⊥AB.
证明:FH⊥AB(已知)
∴∠BHF=
.
∵∠1=∠ACB(已知)
∴DE∥BC(
)
∴∠2=
.(
)
∵∠2=∠3(已知)
∴∠3=
.(
)
∴CD∥FH(
)
∴∠BDC=∠BHF=
.
(
)
∴CD⊥AB
20.(8分)如图,∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,
试判断
OD与
OE的位置关系,并说明理由.
21.(8分)如图,已知∠1+∠2=180°,∠A=∠C,证明:AB∥CD.
22.(8分)如图,直线AB、CD相交于点O,OE把分成两部分,
(1)直接写出图中的对顶角为________,的邻补角为________;
(2)若,且=2:3,求的度数.
23.(11分)如图,,
(1)问直线与有怎样在位置关系?并说明理由;
(2)若
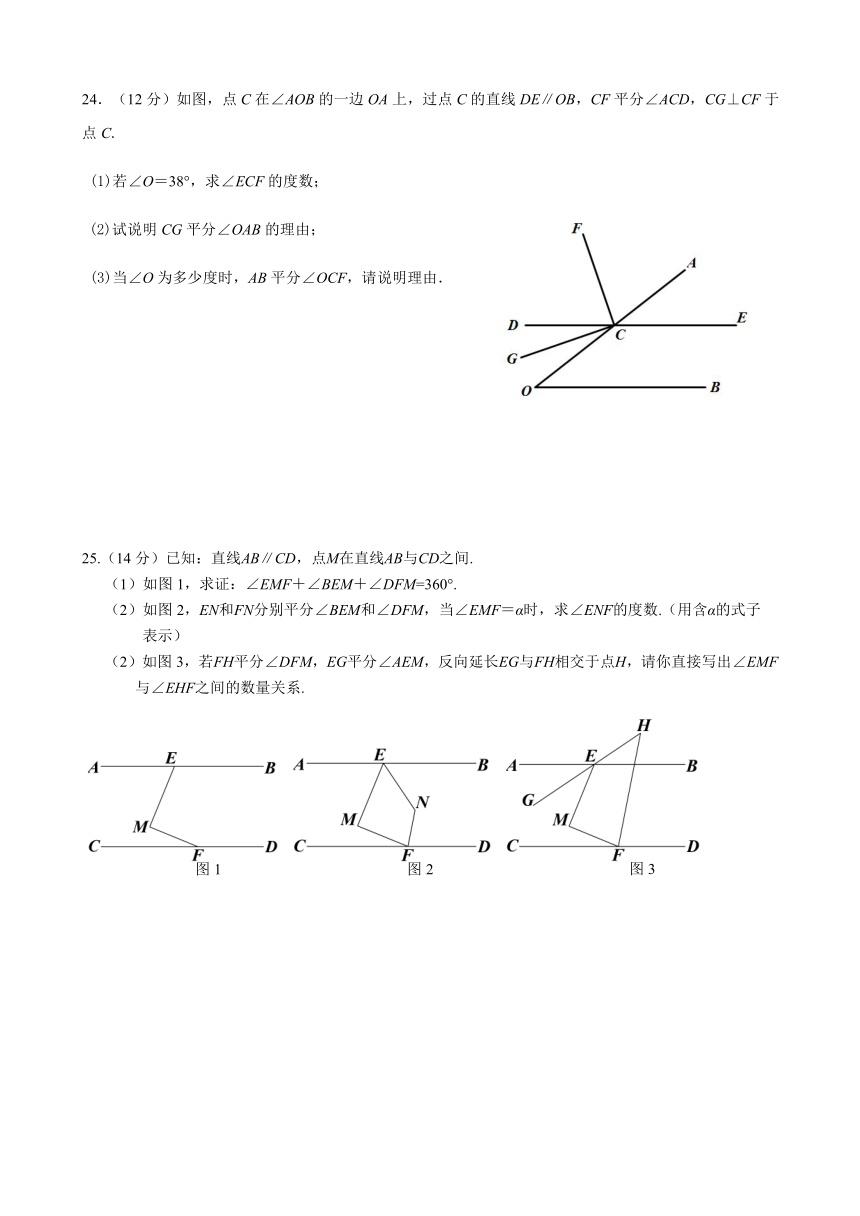
24.(12分)如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=38°,求∠ECF的度数;
(2)试说明CG平分∠OAB的理由;
(3)当∠O为多少度时,AB平分∠OCF,请说明理由.
25.(14分)已知:直线AB∥CD,点M在直线AB与CD之间.
(1)如图1,求证:∠EMF+∠BEM+∠DFM=360°.
(2)如图2,EN和FN分别平分∠BEM和∠DFM,当∠EMF=α时,求∠ENF的度数.(用含α的式子
表示)
(2)如图3,若FH平分∠DFM,EG平分∠AEM,反向延长EG与FH相交于点H,请你直接写出∠EMF
与∠EHF之间的数量关系.
(
图
1
)
(
图
2
)
(
图
3
)
参考答案:
1-10
BCBDD
AACDD
11.50°
12.垂线段最短
13.a∥c
14.18°或66°
15.如果两个角是领补角,那么它们互补.
16.6
17.(1)证明:∵∠1=∠2,∠3=∠2
∴∠1=∠3
则a∥b
(2)∵
∴∠1=∠3
∵∠3=∠2
∴∠1=∠2
18.(1)略
(2)平行且相等
(3)4
19.证明:FH⊥AB(已知)
∴∠BHF=90°
∵∠1=∠ACB(已知)
∴DE∥BC(同位角相等,两直线平行)
∴∠2=∠BCD。(两直线平行,内错角相等)
∵∠2=∠3(已知)
∴∠3=∠BCD。(等量代换)
∴CD∥FH(同位角相等,两直线平行)
∴∠BDC=∠BHF=90°(两直线平行,同位角相等)
∴CD⊥AB
20.OD与OE互相垂直.理由如下:
∵OD是∠AOC的平分线,∴∠COD=∠AOC,
∵OE是∠BOC的平分线,∴∠COE=∠BOC.
∵∠AOC+∠BOC=180°,
∠AOC+∠BOC=90°,
∴∠COD+∠COE=90°,即∠DOE=90°.
∴OD⊥OE.
21.证明:?
∵∠1+∠2=180°(已知)
∴AD∥BC(同旁内角互补,两直线平行)
∴∠EDA=∠C(两直线平行,同位角相等)
又∵∠A=∠C(已知)
∴∠A=∠EDA(等量代换)
∴AB∥CD(内错角相等,两直线平行)
22.(1)∠BOD,∠AOE
(2)152°
23.
(1)EF和AB的关系为平行关系。理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC-∠CBF=50°,
∵∠EFB=130°,∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵CEF=70°,
∴∠ECD=110°
∵∠DCB=70°
∴∠ACB=∠ECD-∠DCB,
∴∠ACB=40°
24.
(1)∵DE∥OB∴∠O=∠ACE,
∵∠O=38°∴∠ACE=38°
∵∠ACD+∠ACE=180°
∴∠ACD=142°
又∵CF平分∠ACD
∴∠ACF=∠DCF=71°
∴∠ECF=109°
证明:
∵CG⊥CF
∴∠FCG=90°
∴∠DCF+∠DCG=90°
又∵∠GCO+∠GCD+∠FCA+∠FCD=180°
∴∠GCO+∠FCA=90°
∵∠ACF=∠FDC
∴∠GCO=∠DCG
即CG平分∠OCD
结论:当∠O=60°时,CD平分∠OCF
当∠O=60°时
∵DE∥OB
∴∠DCO=∠O=60°
∴∠ACD=120°
又∵CF平分∠ACD
∴∠DCF=60°
∴∠DCO=∠DCF
即CD平分∠OCF
25.解答:(1)如图,过M作MK∥AB
∵MK∥AB
∴∠1+∠3=180°①
∵AB∥CD
∴MK∥CD
则∠2+∠4=180°②
由①+②得:∠1+∠2+∠3+∠4=360°
即∠EMF+∠BEM+∠DFM=360°.
(2)如图,过N作NP∥AB
由(1)得∠EMF+∠BEM+∠DFM=360°
∵∠EMF=α
∴∠BEM+∠DFM=360°-α
∵EN和FN分别平分∠BEM和∠DFM
∴∠5=∠BEM,∠6=∠DFM,
∴∠5+∠6==
∵NP∥AB
∴∠5=∠ENP①
∵AB∥CD
∴NP∥CD
则∠6=∠DEN②
由①+②得:∠5+∠6=∠ENP+∠DEN
即∠ENF=∠5+∠6=180°-α
(3)∠EMF+2∠EHF=180°.
一、选择题(每小题4分,共40分)
1.下列图形可以由一个图形经过平移变换得到的是(
)
A
.
B.
C.
D.
2.在下列图形中,由∠1=∠2
能得到
AB∥CD
的是(
)
A
.
B.
C.
D.
3.对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A
.
a=3,b=2
B.
a=﹣3,b=2
C.
a=3,b=﹣1
D.
a=﹣1,b=3
4.如图,下列判断中错误的是(
)
A
.∠A与∠1是同位角
B.∠A与∠B是同旁内角
C.∠4与∠1是内错角
D.∠1与∠3是同位角
5.如图,∠BAC=90°,AD⊥BC于点D,则下列结论中错误的是(
)
A.点C到AB的垂线段是线段AC
B.点A到BC的距离是线段AD的长度
C.线段AB的长度是点B到AC的距离
D.线段AB是点B到AC的距离
(
第
4
题图
)
(
第
6
题图
)
(
第
5
题图
)
6.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
7.下列说法正确的个数是?( )
①同位角相等;?
②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
A
.
1个
B.
2个
C.
3个
D.
4个
8.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A、D两点分别与对应,
若∠1=2∠2,则∠AEF的度数为( )
A
.
60°
B.
65°
C.
72°
D.
75°
9.如图,∠1=68°,直线a平移后得到直线b,则∠2﹣∠3的度数为( )
A
.
78°
B.132°
C.
118°
D.
112°
(
第
9
题图
)
(
第
10
题图
)
(
第
8
题图
)
10.如图,AB∥CD,则下列各式中正确的是( )
A.∠1=180°-∠3
B.∠1=∠3-∠2
C.∠2+∠3=180°-∠1
D.∠2+∠3=180°+∠1
二、填空题(每小题4分,共24分)
11.
直线AB、CD相交于点O,若∠AOC=50°,则∠BOD= ??
。
12.
如图,测量运动员跳远成绩选取的是AB的长度,其依据是.
(
第
12
题图
)13.
若直线a⊥b,
b⊥c,则直线a与c的位置关系是.
14.若
.
15.
把命题“邻补角互补”改成“如果……那么……”形式:
.
16.
如图,将面积为2的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,
那么图中的四边形ACED的面积为________.
(
第
16
题图
)三、解答题(共86分)
17.(8分)(1)如图,已知∠1=∠2,求证:a∥b.
(2)如图,直线,求证:.
(8分)在网格上,平移三角形ABC,并将三角形ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形三角形DEF;
(2)线段AD与线段BE的关系是;
(3)三角形DEF的面积是
.
19.
(9分)阅读理解并在括号内填注理由:
已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.求证:CD⊥AB.
证明:FH⊥AB(已知)
∴∠BHF=
.
∵∠1=∠ACB(已知)
∴DE∥BC(
)
∴∠2=
.(
)
∵∠2=∠3(已知)
∴∠3=
.(
)
∴CD∥FH(
)
∴∠BDC=∠BHF=
.
(
)
∴CD⊥AB
20.(8分)如图,∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,
试判断
OD与
OE的位置关系,并说明理由.
21.(8分)如图,已知∠1+∠2=180°,∠A=∠C,证明:AB∥CD.
22.(8分)如图,直线AB、CD相交于点O,OE把分成两部分,
(1)直接写出图中的对顶角为________,的邻补角为________;
(2)若,且=2:3,求的度数.
23.(11分)如图,,
(1)问直线与有怎样在位置关系?并说明理由;
(2)若
24.(12分)如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=38°,求∠ECF的度数;
(2)试说明CG平分∠OAB的理由;
(3)当∠O为多少度时,AB平分∠OCF,请说明理由.
25.(14分)已知:直线AB∥CD,点M在直线AB与CD之间.
(1)如图1,求证:∠EMF+∠BEM+∠DFM=360°.
(2)如图2,EN和FN分别平分∠BEM和∠DFM,当∠EMF=α时,求∠ENF的度数.(用含α的式子
表示)
(2)如图3,若FH平分∠DFM,EG平分∠AEM,反向延长EG与FH相交于点H,请你直接写出∠EMF
与∠EHF之间的数量关系.
(
图
1
)
(
图
2
)
(
图
3
)
参考答案:
1-10
BCBDD
AACDD
11.50°
12.垂线段最短
13.a∥c
14.18°或66°
15.如果两个角是领补角,那么它们互补.
16.6
17.(1)证明:∵∠1=∠2,∠3=∠2
∴∠1=∠3
则a∥b
(2)∵
∴∠1=∠3
∵∠3=∠2
∴∠1=∠2
18.(1)略
(2)平行且相等
(3)4
19.证明:FH⊥AB(已知)
∴∠BHF=90°
∵∠1=∠ACB(已知)
∴DE∥BC(同位角相等,两直线平行)
∴∠2=∠BCD。(两直线平行,内错角相等)
∵∠2=∠3(已知)
∴∠3=∠BCD。(等量代换)
∴CD∥FH(同位角相等,两直线平行)
∴∠BDC=∠BHF=90°(两直线平行,同位角相等)
∴CD⊥AB
20.OD与OE互相垂直.理由如下:
∵OD是∠AOC的平分线,∴∠COD=∠AOC,
∵OE是∠BOC的平分线,∴∠COE=∠BOC.
∵∠AOC+∠BOC=180°,
∠AOC+∠BOC=90°,
∴∠COD+∠COE=90°,即∠DOE=90°.
∴OD⊥OE.
21.证明:?
∵∠1+∠2=180°(已知)
∴AD∥BC(同旁内角互补,两直线平行)
∴∠EDA=∠C(两直线平行,同位角相等)
又∵∠A=∠C(已知)
∴∠A=∠EDA(等量代换)
∴AB∥CD(内错角相等,两直线平行)
22.(1)∠BOD,∠AOE
(2)152°
23.
(1)EF和AB的关系为平行关系。理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC-∠CBF=50°,
∵∠EFB=130°,∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵CEF=70°,
∴∠ECD=110°
∵∠DCB=70°
∴∠ACB=∠ECD-∠DCB,
∴∠ACB=40°
24.
(1)∵DE∥OB∴∠O=∠ACE,
∵∠O=38°∴∠ACE=38°
∵∠ACD+∠ACE=180°
∴∠ACD=142°
又∵CF平分∠ACD
∴∠ACF=∠DCF=71°
∴∠ECF=109°
证明:
∵CG⊥CF
∴∠FCG=90°
∴∠DCF+∠DCG=90°
又∵∠GCO+∠GCD+∠FCA+∠FCD=180°
∴∠GCO+∠FCA=90°
∵∠ACF=∠FDC
∴∠GCO=∠DCG
即CG平分∠OCD
结论:当∠O=60°时,CD平分∠OCF
当∠O=60°时
∵DE∥OB
∴∠DCO=∠O=60°
∴∠ACD=120°
又∵CF平分∠ACD
∴∠DCF=60°
∴∠DCO=∠DCF
即CD平分∠OCF
25.解答:(1)如图,过M作MK∥AB
∵MK∥AB
∴∠1+∠3=180°①
∵AB∥CD
∴MK∥CD
则∠2+∠4=180°②
由①+②得:∠1+∠2+∠3+∠4=360°
即∠EMF+∠BEM+∠DFM=360°.
(2)如图,过N作NP∥AB
由(1)得∠EMF+∠BEM+∠DFM=360°
∵∠EMF=α
∴∠BEM+∠DFM=360°-α
∵EN和FN分别平分∠BEM和∠DFM
∴∠5=∠BEM,∠6=∠DFM,
∴∠5+∠6==
∵NP∥AB
∴∠5=∠ENP①
∵AB∥CD
∴NP∥CD
则∠6=∠DEN②
由①+②得:∠5+∠6=∠ENP+∠DEN
即∠ENF=∠5+∠6=180°-α
(3)∠EMF+2∠EHF=180°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
